
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурная и приведенная формы экономической модели. Условия индетификации.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Система уравнений (3.1) называется структурной формой модели, а ее коэффициенты – структурными коэффициентами. Система (3.2) называется приведенной формой модели. Обозначим
Тогда систему уравнений (3.2) можно переписать в виде
В системе (3.3) объясняющая переменная х1 является экзогенной переменной и, следовательно, независима со случайными компонентами v1 и v2. Метод наименьших квадратов дает состоятельные оценки Очевидно, что Такой метод построения оценок структурных коэффициентов с помощью оценок коэффициентов приведенной формы называется косвенным методом наименьших квадратов. Вместе с тем, коэффициенты В общем случае под идентифицируемостью понимают возможность определения структурных коэффициентов уравнений по коэффициентам приведенной формы. Проблема идентификации – это проблема единственности соответствия между приведенной и структурной формами. Приведенная форма в полном виде имеет nm параметров, а структурная – n(n-1+m) параметров. Ясно, что n(n-1+m) оценокпараметров структурной формы в общем случае невозможно получить единственным образом на основе nm параметров приведенной формы. Необходимое условие идентифицируемости – выполнение следующего правила:
где Н – число эндогенных переменных в уравнении; D – число предопределенных переменных системы, отсутствующих в уравнении. Для сверхидентифицированных уравнений используется двухшаговый метод наименьших квадратов, который заключается в следующем: – составляют приведенную форму модели и определяют ее параметры обычным МНК; – выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, и находят их расчетные значения по соответствующим уравнениям приведенной формы модели; – обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных расчетные значения эндогенных переменных, стоящих в правой части структурного уравнения.
Пример Имеется следующая система структурных уравнений
Приведенная система уравнений после оценки параметров методом наименьших квадратов имеет вид
Для первого уравнения H=2, D=1 (отсутствует х4) и Для второго уравнения H=2, D=1 (отсутствует х2) и Чтобы получить первое структурное уравнение из 1-го приведенного, выразим отсутствующий признак х4 из 2-го приведенного уравнения:
После подстановки х4 в первое приведенное уравнение и преобразований, получим
Для определения параметров 2-го структурного уравнения выразим отсутствующий во 2-м структурном уравнении фактор х2 из 1-го приведенного уравнения:
После подстановки х2 во второе приведенное уравнение, получим
Задание 2 Построить модель вида
рассчитав соответствующие структурные коэффициенты. Система приведенных уравнений имеет вид
Значения коэффициентов
АНАЛИЗ ВРЕМЕННЫХ РЯДОВ И ПРОГНОЗИРОВАНИЕ Анализ временных рядов Временной ряд представляет собой ряд числовых значений какого-либо показателя в последовательные моменты или периоды времени. Числовые значения, составляющие временной ряд, называются уровнями ряда. По способу построения ряд может быть моментным, когда уровни ряда представлены на определенные моменты времени (конец квартала, начало года и т.д.) и интервальным, когда уровни ряда соответствуют определенным интервалам времени. Изучение различных процессов на основе временных рядов включает следующие этапы: – сбор исходной информации и построение временных рядов; – визуальный анализ временного ряда и формирование набора возможных моделей прогнозирования; – идентификация (подбор) модели; – оценка параметров моделей; – осуществление прогноза по математической модели. В практике анализа временных рядов принято считать, что значения уровней временных рядов складываются из следующих компонент:
– тренд; – сезонная составляющая; – циклическая составляющая; – случайная составляющая. Под трендом (тенденцией) понимают изменения, определяющие общее направление развития изучаемого показателя. Это систематическая составляющая долговременного действия. Для описания тренда используют плавно меняющиеся, гладкие функции. Наряду с долговременными тенденциями во временных рядах часто имеют место более или менее регулярные колебания – периодические составляющие рядов динамики. Если период колебаний не превышает одного года, то их называют сезонными. Причины сезонных колебаний могут быть связаны с природно-климатическими условиями, могут носить социальный характер (например, увеличение покупок в выходные дни, увеличение платежей в конце квартала и т. д.). Для описания сезонной компоненты используют периодические функции. При большом периоде колебаний считают, что во временных рядах имеется циклическая составляющая. Примерами могут служить демографические, деловые, инвестиционные и другие циклы. Если из временного ряда удалить тренд и периодические составляющие, то останется нерегулярная компонента. Часто причиной нерегулярных колебаний является действие большого числа различных факторов. Эта компонента рассматривается как случайная.
Критерий случайности Одним из первых вопросов при анализе временного ряда является вопрос о наличии или отсутствии тренда. Для решения этого вопроса со статистических позиций используют различные тесты на случайность. Один из наиболее простых критериев состоит в подсчете количества «пиков» или «ям» в ряде. «Пик» есть значение, которое больше двух соседних, а «яма» – значение, которое меньше двух соседних. «Пики» и «ямы» называются экстремальными точками или «точками поворота». Интервал монотонности между двумя экстремальными точками называют «фазой». Чтобы определить экстремальную точку, требуется 3 последовательных уровня ряда. Если бы ряд был случаен, то вероятность появления экстремальной точки была бы равна 2/3 (четыре варианта из 3!). Рассмотрим временной ряд
Тогда число экстремальных точек
В предположении случайности ряда математическое ожидание случайной величины Р составит
Кроме того, можно показать, что
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.26 (0.009 с.) |

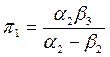 ;
;  ;
; 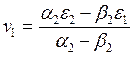 ;
;  .
.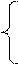
 , (3.3)
, (3.3)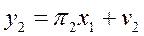 .
. и
и 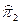 .
.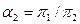 . Можно показать, что
. Можно показать, что  будет состоятельной оценкой структурного коэффициента
будет состоятельной оценкой структурного коэффициента 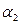 .
. и
и 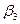 не могут быть найдены, т. е. они неидентифицируемые.
не могут быть найдены, т. е. они неидентифицируемые.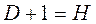 – уравнение идентифицируемое;
– уравнение идентифицируемое;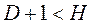 – уравнение неидентифицируемое;
– уравнение неидентифицируемое;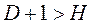 – уравнение сверх идентифицируемое,
– уравнение сверх идентифицируемое,
 ;
;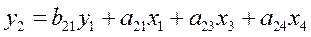 .
.
 ,
, .
. .
.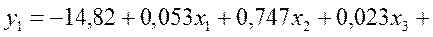

 .
.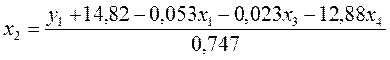 .
.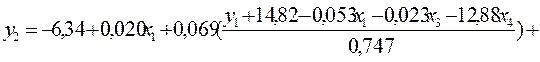

 ,
, ,
,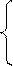
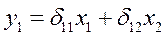 ,
, .
. приведены в таблице.
приведены в таблице.

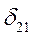
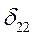
 и введем переменную
и введем переменную  следующим образом (i=1,2, …, n-2):
следующим образом (i=1,2, …, n-2): , если
, если 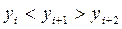 или
или  ;
;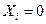 в противном случае.
в противном случае.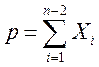 .
.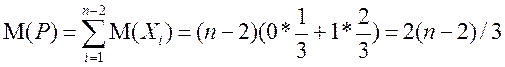 .
.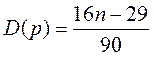 .
.


