
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первое уравнение системы (2.15) можно преобразовать к видуСодержание книги
Поиск на нашем сайте
или
Второе уравнение можно преобразовать к виду
Таким образом, мы имеем систему уравнений
Разделив обе части уравнений (2.16) на n, получим систему уравнений в виде
где соответствующие средние определяются по формулам
Подставляя значение
где
Отметим, что линия регрессии проходит через точку
В заключение приведем удобные для расчета оценок параметров формулы:
Если рассчитан выборочный коэффициент корреляции
где
В качестве оценки дисперсии случайной компоненты
При выполнении предположений 1-4 доказано, что оценки параметров Кроме того, статистика Проверка статистической значимости оценок коэффициентов регрессии В действительности может оказаться, что фактор X не влияет на результирующий признак Y, что эквивалентно условию Проверка значимости оценок с помощью критерия Стьюдента проводится путем сопоставления вычисленных значений оценок с величиной их среднего квадратичного отклонения. Статистика теста имеет вид
Известно, что дисперсия оценки
Поэтому для вычисления оценки
Если Использование регрессионной модели для прогноза. Дисперсия ошибки прогноза Основное назначение регрессионной модели – использование ее для прогноза экономического показателя Y. Прогноз осуществляется подстановкой значения фактора
Построим доверительный интервал для функции регрессии, т. е. для условного математического ожидания М(Y/xl), который с заданной надежностью (доверительной вероятностью) Р = 1- Найдем дисперсию прогноза
Дисперсия
Здесь учтено, что Дисперсия выборочной средней
Для нахождения дисперсии
Найдем оценку дисперсии
Основываясь на предпосылках 1–5 регрессионного анализа, можно показать, что статистика
имеет распределение Стьюдента с ν = n-2 степенями свободы и построить доверительный интервал для условного математического ожидания
Из формул (2.33) и (2.34) видно, что величина доверительного интервала зависит от значения объясняющей переменной Ошибку прогноза можно представить следующим образом:
Первая скобка представляет собой ошибку, вызванную наличием случайной составляющей ε. Ее дисперсия равна Вторая скобка представляет собой ошибку оценки среднего уровня. Ее дисперсия определяется по формуле (2.33). Таким образом, для оценки дисперсии ошибки прогноза можно пользоваться следующим выражением:
Эта формула учитывает как погрешность оценки Из (2.36) следует, что с ростом
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.102.163 (0.009 с.) |

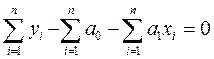
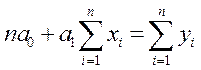 .
. .
.
 ; (2.16)
; (2.16) .
.
 , (2.17)
, (2.17) ,
, ;
;  ;
; ;
;  . (2.18)
. (2.18) из первого уравнения системы (2.17) во второе, получим
из первого уравнения системы (2.17) во второе, получим , (2.19)
, (2.19) – выборочная дисперсия переменной Х:
– выборочная дисперсия переменной Х: , (2.20)
, (2.20)
 – выборочная ковариация:
– выборочная ковариация: . (2.21)
. (2.21) , т. е.
, т. е.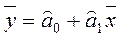 .
.
 , (2.22)
, (2.22) . (2.23)
. (2.23)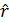 , то коэффициенты a0 и a1 могут быть определены следующим образом:
, то коэффициенты a0 и a1 могут быть определены следующим образом: ,
, 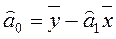 , (2.24)
, (2.24)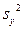 – выборочная дисперсия переменной Y:
– выборочная дисперсия переменной Y: .
.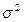 используется
используется . (2.25)
. (2.25) и
и  по методу наименьших квадратов
по методу наименьших квадратов  и
и  являются несмещенными с минимальными дисперсиями в классе линейных оценок (т. е. эффективными).
являются несмещенными с минимальными дисперсиями в классе линейных оценок (т. е. эффективными). является несмещенной оценкой дисперсии
является несмещенной оценкой дисперсии  . Однако при этом
. Однако при этом  . Для проверки существенности отклонения
. Для проверки существенности отклонения  .
. . (2.26)
. (2.26) определяется следующим образом:
определяется следующим образом: . (2.27)
. (2.27) можно использовать следующую формулу:
можно использовать следующую формулу: . (2.28)
. (2.28) , то принимается гипотеза H0, в противном случае принимается гипотеза H1. В случае принятия гипотезы H0 фактор Х исключается из модели и принимается, что
, то принимается гипотеза H0, в противном случае принимается гипотеза H1. В случае принятия гипотезы H0 фактор Х исключается из модели и принимается, что  .
. в оценку детерминированной составляющей:
в оценку детерминированной составляющей: . (2.29)
. (2.29) накрывает неизвестное значение М(Y/xl).
накрывает неизвестное значение М(Y/xl). , представляющего собой выборочную оценку М(Y/xl). С этой целью уравнение (2.29) представим в виде
, представляющего собой выборочную оценку М(Y/xl). С этой целью уравнение (2.29) представим в виде . (2.30)
. (2.30) равна сумме дисперсий двух независимых (доказательство этого факта опускается) слагаемых выражения (2.30).
равна сумме дисперсий двух независимых (доказательство этого факта опускается) слагаемых выражения (2.30). . (2.31)
. (2.31) – неслучайная величина, при вынесении которой за знак дисперсии ее необходимо возвести в квадрат.
– неслучайная величина, при вынесении которой за знак дисперсии ее необходимо возвести в квадрат.
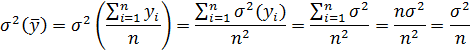 . (2.32)
. (2.32)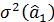 воспользуемся формулой (2.27), т. е.
воспользуемся формулой (2.27), т. е. ее оценкой
ее оценкой  .
.

 . (2.34)
. (2.34) : при
: при  она минимальна, а по мере удаления
она минимальна, а по мере удаления  величина доверительного интервала увеличивается.
величина доверительного интервала увеличивается. . (2.35)
. (2.35) . (2.36)
. (2.36) так и отклонение
так и отклонение 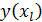 от своего математического ожидания, обусловленное наличием случайной составляющей.
от своего математического ожидания, обусловленное наличием случайной составляющей. дисперсия ошибки прогноза увеличивается.
дисперсия ошибки прогноза увеличивается.


