
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множественная линейная регрессияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной Y от нескольких объясняющих переменных X1, X2, …, Xk. Эта задача решается с помощью множественного регрессионного анализа. Модель множественной линейной регрессии имеет вид
или
(i=1,…,n) (2.43) Модель (2.42), в которой зависимая переменная Включение в регрессионную модель новых объясняющих переменных усложняет получаемые формулы и вычисления. Это приводит к целесообразности использования матричных обозначений. Введем обозначения:
Х = – матрица значений объясняющих переменных размера n(k+1). где xij – значение j -й переменной для i -го объекта выборки. Обращаем внимание на то, что в матрицу Х дополнительно введен столбец, все элементы которого равны 1, т. е. условно полагается, что в модели (2.42) свободный член
Тогда в матричном виде модель (2.42) примет вид
Как уже было отмечено, модель (2.44), удовлетворяющая приведенным предпосылкам 1–5, называется классической нормальной линейной моделью множественной регрессии. Если же среди приведенных предпосылок не выполняется лишь предпосылка 5 о нормальном законе распределения вектора возмущений ε, то модель (2.44) называется просто классической линейной моделью множественной регрессии. Оценки параметров а0, a1, … ak можно получить с помощью рассмотренного ранее метода наименьших квадратов. Система уравнений имеет вид
……..
Суммирование производится по индексу i от 1 до n, где n – объем выборки. Эту систему обычно записывают в матричном виде
где Умножив обе части уравнения слева на матрицу
Оценки, полученные с помощью МНК, являются случайными величинами, так как представляют собой линейную комбинацию случайных величин у1, у2, … уn. При выполнении предпосылок множественного регрессионного анализа оценка метода наименьших квадратов Преобразуем вектор оценок (2.45) с учетом (2.44):
или
т. е. оценки параметров (2.45), найденные по выборке, будут содержать случайные ошибки. Покажем, что математическое ожидание оценки
так как Вариации оценок параметров будут в конечном счете определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают так называемую ковариационную матрицу оценок параметров
где
Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных. В силу того, что оценки
Рассматривая ковариационную матрицу
В матричном виде ковариационная матрица вектора оценок параметров
(в этом легко убедиться, перемножив векторы Учитывая (2.46), преобразуем это выражение:
ибо элементы матрицы Х – неслучайные величины.
в которой все элементы, не лежащие на главной диагонали, равны нулю в силу предпосылки о некоррелированности возмущений
Поэтому матрица
где
или Итак, с помощью обратной матрицы Прогноз по модели множественной линейной регрессии для вектора переменных
Дисперсия ошибки прогноза определяется по формуле
В качестве оценки
Тогда оценка дисперсии ошибки прогноза
Качество всей модели в целом определяется по критерию Фишера
Если Может быть рассчитан коэффициент детерминации, отражающий долю объясненной факторами дисперсии в общей дисперсии:
Правило проверки статистической значимости оценок Н0: Для этого вычисляется статистика
которая при выполнении гипотезы Н0 распределена по закону Стьюдента с n-k-1 степенями свободы. Если
2.7. Некоторые вопросы практического применения Регрессионных моделей
Ранее нами была изучена классическая линейная модель множественной регрессии. Однако мы не касались некоторых проблем, связанных с практическим использованием модели множественной регрессии. К их числу относится мультиколлинеарность. Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных. Мультиколлинеарность может проявляться в функциональной и стохастической формах. При функциональной форме мультиколлинеарности по крайней мере одна из парных связей между объясняющими переменными является линейной функциональной зависимостью. В этом случае матрица ХTX особенная, так как содержит линейно зависимые векторы-столбцы и ее определитель равен нулю. Это приводит к невозможности решения соответствующей системы уравнений и получения оценок параметров регрессионной модели. Однако в экономических исследованиях мультиколлинеарность чаще всего проявляется в стохастической форме, когда между хотя бы двумя объясняющими переменными существует тесная корреляционная связь. Матрица ХTX в этом случае является неособенной, но ее определитель очень мал. В результате получаются значительные дисперсии оценок коэффициентов регрессии Наличие мультиколлинеарности системы объясняющих переменных можно статистически проверить по тесту Глобера – Феррара. При отсутствии мультиколлинеарности статистика
где
det Вычисленное значение Одним из методов снижения мультиколлинеарности системы объясняющих переменных X1, X2, …, Xk является выявление пар переменных с высокими коэффициентами корреляции (более 0,8). При этом одну из таких переменных исключают из рассмотрения. Какую из двух переменных удалить решают на основании экономических соображений или оставляют ту, которая имеет более высокий коэффициент корреляции с зависимой переменной.
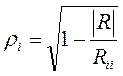
Полезно также находить множественные коэффициенты корреляции между одной объясняющей переменной и некоторой группой из них. Множественный коэффициент корреляции служит мерой линейной зависимости между случайной величиной Хi и некоторым набором других случайных величин X1, X2, X3, …,Xi-1,Xi+1,… Xk. Множественный коэффициент корреляции Чем ближе значения коэффициента множественной корреляции к единице, тем лучше приближение случайной величины Хi линейной комбинацией случайных величин X1, X2, X3, …,Xi-1,Xi+1,… Xk. Множественный коэффициент корреляции выражается через элементы корреляционной матрицы следующим образом:
где │R│– определитель корреляционной матрицы R; Rii – алгебраическое дополнение элемента rii. Если С другой стороны, В качестве выборочной оценки коэффициента множественной корреляции используется выражение
Наличие высокого множественного коэффициента корреляции (более 0,8) также свидетельствует о мультиколлинеарности. Еще одним из методов уменьшения мультиколлинеарности является использование пошаговых процедур отбора наиболее информативных переменных с использованием скорректированного коэффициента детерминации. Недостатком коэффициента детерминации R2 для выбора наилучшего уравнения регрессии является то, что он всегда увеличивается при добавлении новых переменных в регрессионную модель. Поэтому целесообразно использовать скорректированный коэффициент детерминации
В отличие от R2 скорректированный коэффициент На первом шаге рассматривается лишь одна объясняющая переменная, имеющая с зависимой переменной Y наибольший коэффициент корреляции (детерминации). На втором шаге включается в регрессию новая объясняющая переменная, которая вместе с первоначальной дает наиболее высокий скорректированный коэффициент детерминации с Y ит. д.
Процедура введения новых переменных продолжается до тех пор, пока будет увеличиваться скорректированный коэффициент детерминации
|
||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1063; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.255.180 (0.009 с.) |

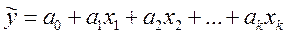 ;
; 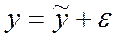 (2.42)
(2.42) ;
; 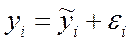 .
.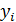 , возмущения
, возмущения 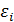 и объясняющие переменные
и объясняющие переменные 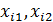 ,…,
,…, 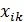 удовлетворяют приведенным выше предпосылкам 1–5 регрессионного анализа, называется классической нормальной линейной моделью множественной регрессии.
удовлетворяют приведенным выше предпосылкам 1–5 регрессионного анализа, называется классической нормальной линейной моделью множественной регрессии.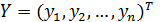 – вектор-столбец значений зависимой переменной размера n;
– вектор-столбец значений зависимой переменной размера n;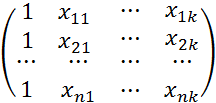
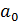 умножается на фиктивную переменную
умножается на фиктивную переменную 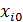 , принимающую значение 1 для всех i:
, принимающую значение 1 для всех i: 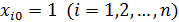 ;
;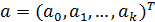 – вектор-столбец параметров размером k+1;
– вектор-столбец параметров размером k+1;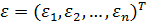 – вектор-столбец возмущений (случайных ошибок, остатков) размера n.
– вектор-столбец возмущений (случайных ошибок, остатков) размера n.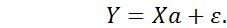 (2.44)
(2.44)
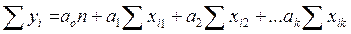 ,
,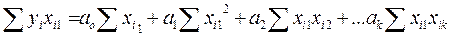 ,
,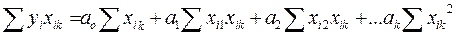 .
.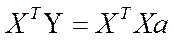 ,
,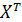 – транспонированная матрица.
– транспонированная матрица.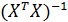 , получим
, получим . (2.45)
. (2.45)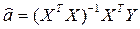 является эффективной, т. е. обладает наименьшей дисперсией в классе линейных несмещенных оценок.
является эффективной, т. е. обладает наименьшей дисперсией в классе линейных несмещенных оценок.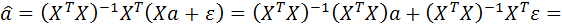
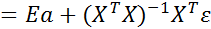
 =
= 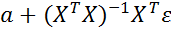 , (2.46)
, (2.46)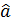 равно оцениваемому параметру
равно оцениваемому параметру 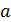 :
: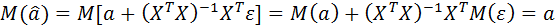 ,
, . Таким образом, очевидно, что вектор
. Таким образом, очевидно, что вектор 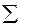 :
: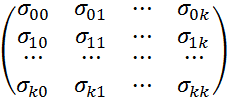 ,
,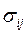 – ковариации оценок параметров
– ковариации оценок параметров 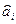 и
и 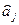 . Ковариация двух переменных определяется как математическое ожидание произведения отклонений этих переменных от их математических ожиданий. Поэтому
. Ковариация двух переменных определяется как математическое ожидание произведения отклонений этих переменных от их математических ожиданий. Поэтому . (2.47)
. (2.47) , т. е.
, т. е. 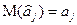 , выражение (2.47) примет вид
, выражение (2.47) примет вид .
. . (2.48)
. (2.48)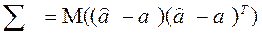
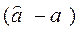 и
и 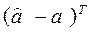 ).
).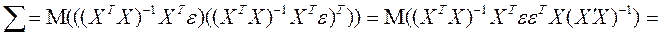
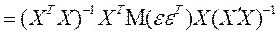 (2.49)
(2.49) Матрица
Матрица 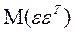 представляет собой ковариационную матрицу вектора возмущений:
представляет собой ковариационную матрицу вектора возмущений: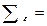
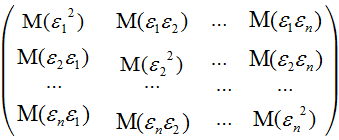 ,
,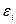 и
и 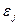 между собой, а все элементы, лежащие на главной диагонали, в силу предпосылок регрессионного анализа равны одной и той же дисперсии
между собой, а все элементы, лежащие на главной диагонали, в силу предпосылок регрессионного анализа равны одной и той же дисперсии 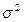 :
: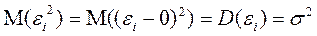 .
.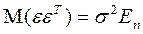 ,
, – единичная матрица n -го порядка. Следовательно, в силу (2.49) ковариационная матрица вектора оценок параметров:
– единичная матрица n -го порядка. Следовательно, в силу (2.49) ковариационная матрица вектора оценок параметров: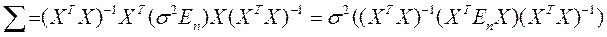
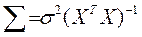 . (2.50)
. (2.50)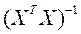 определяется не только сам вектор
определяется не только сам вектор 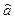 оценок параметров, но и дисперсии и ковариации его компонент.
оценок параметров, но и дисперсии и ковариации его компонент.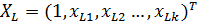 составит
составит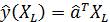 . (2.51)
. (2.51)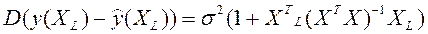 . (2.52)
. (2.52)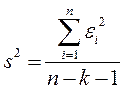 . (2.53)
. (2.53)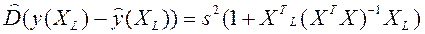 . (2.54)
. (2.54)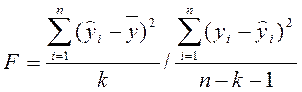 . (2.55)
. (2.55)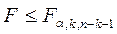 , то уравнение регрессии в целом незначимо. Здесь
, то уравнение регрессии в целом незначимо. Здесь  – табличное значение критерия Фишера с k и n-k-1 степенями свободы уровня значимости
– табличное значение критерия Фишера с k и n-k-1 степенями свободы уровня значимости  .
.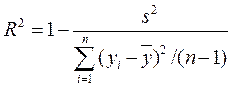 . (2.56)
. (2.56)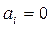 .
.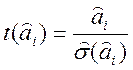 , (2.57)
, (2.57) , гипотезу Н0 следует отклонить и признать коэффициент
, гипотезу Н0 следует отклонить и признать коэффициент 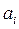 статистически значимым. В противном случае следует признать
статистически значимым. В противном случае следует признать 
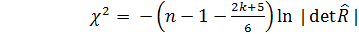 , (2.58)
, (2.58)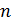 – объем выборки;
– объем выборки;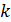 – количество объясняющих переменных;
– количество объясняющих переменных;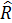 – определитель выборочной корреляционной матрицы объясняющих переменных
– определитель выборочной корреляционной матрицы объясняющих переменных 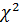 – распределение с k(k-1)/2 степенями свободы.
– распределение с k(k-1)/2 степенями свободы.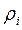 определяется как обычный коэффициент парной корреляции между Хi и Хi*, где Хi* − наилучшее линейное приближение Хi случайными величинами X1, X2, X3, …,Xi-1,Xi+1,… Xk.
определяется как обычный коэффициент парной корреляции между Хi и Хi*, где Хi* − наилучшее линейное приближение Хi случайными величинами X1, X2, X3, …,Xi-1,Xi+1,… Xk.
 , (2.59)
, (2.59) , то величина Хi представляет собой линейную комбинацию случайных величин X1, X2, X3, …,Xi-1,Xi+1,… Xk.
, то величина Хi представляет собой линейную комбинацию случайных величин X1, X2, X3, …,Xi-1,Xi+1,… Xk. только тогда, когда Хi не коррелированна ни с одной из случайных величин X1, X2, X3, …,Xi-1,Xi+1,… Xk.
только тогда, когда Хi не коррелированна ни с одной из случайных величин X1, X2, X3, …,Xi-1,Xi+1,… Xk.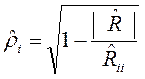 . (2.60)
. (2.60) , определяемый по формуле
, определяемый по формуле .
.


