
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель с цикличностью развитияСодержание книги
Поиск на нашем сайте
Наиболее распространенный подход к построению математических моделей прогнозирования циклических процессов заключается в первоначальном выделении тренда и анализе остаточного ряда в целях выявления и описания периодической компоненты. Для выделения тренда можно использовать процедуру сглаживания временных рядов с помощью метода скользящего среднего. При анализе сезонных колебаний задача упрощается за счет того, что мы знаем их период – 1 год (это относится и к другим циклическим процессам с постоянным и известным периодом). Скользящая средняя, применяемая для этой цели, должна иметь строго определенный период скольжения – 12 месяцев или 4 квартала. При этом индекс сезонности можно определить как отношение фактического уровня ряда к уровню, рассчитанному по скользящей средней. Очевидно, что значения индекса сезонности для данного месяца (квартала) будут различаться из года в год. Поэтому в качестве индекса сезонности следует использовать среднее значение индексов, полученных за ряд лет по одноименным месяцам или кварталам. Однако полученные при этом данные относятся к интервалам с серединами между кварталами, а не к серединам интервалов (15 февраля, 15 мая, 15 августа, 15 ноября). Поэтому необходимо «центрировать» среднее. Наиболее просто это можно сделать, взяв средние последовательных пар средних, вычисленных по 4-м элементам. Такой процесс эквивалентен вычислению средних пяти элементов с весами [ Если средний индекс сезонности за 12 месяцев или 4 квартала не равен единице, производится выравнивание индексов сезонности – деление всех индексов на их средний индекс. Отметим, разумно считать, что влияние сезонности носит мультипликативный характер. В этом случае
где sq – индекс сезонности; gt – трендовая составляющая временного ряда. ПРИМЕР. В табл. 4.5 представлены поквартальные данные о количестве реализованных единиц товара за три года. Т а б л и ц а 4. 5. Данные о реализации товара
Сначала следует оценить тренд. Для этого к данным табл. 4.5 подберем линейную модель тренда по методу наименьших квадратов.
Результаты расчетов трендовых значений для t = 1,..,12 представлены в пятом столбце таблицы. Произведем оценку сезонной составляющей модели как отношение фактического размера реализации к значению тренда. Результаты расчетов приведены в последнем столбце таблицы. Полученные оценки сезонной компоненты пока еще не пригодны для построения прогнозов, поскольку они показывают сезонное отклонение от тренда для конкретного периода времени. Для того чтобы оценки сезонности можно было использовать в целях получения прогноза, скорректированного с учетом сезонных изменений, необходимо найти средние оценки сезонной компоненты. Рассчитаем средние индексы сезонности. Для первого квартала индекс сезонности равен
Для второго квартала
Для третьего квартала
Для четвертого квартала
Взаимная погашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по отдельным периодам должна быть равна числу периодов в цикле. В нашем примере число периодов в цикле равно 4. Найдем сумму средних оценок сезонной компоненты:
Полученные значения индексов сезонности не требуют корректировки и могут использоваться в моделях прогнозов. Найдем прогноз на четвертый год. Для первого квартала (t=13) прогноз размера реализации равен
Для второго квартала
Для третьего квартала
Для четвертого квартала
4.10. Диагностическая проверка адекватности моделей. Критерий Дарбина – Уотсона
Формально качество модели определяется ее адекватностью и точностью прогноза. Модель считается адекватной, если ряд остатков Для проверки свойства нулевого среднего рассчитывается среднее значение остатков:
Если
Гипотеза принимается, если
где
Далее осуществляется проверка остаточного ряда по критерию случайности. Проверка независимости последовательных остатков
Несложные вычисления позволяют проверить, что статистика Дарбина – Уотсона следующим образом связана с выборочным коэффициентом корреляции между соседними наблюдениями.
В самом деле
При большом числе наблюдений n сумма
откуда и следует приближенное равенство (4.52), так как в силу условия
Естественно, что в случае отсутствия автокорреляции выборочный коэффициент Для рядов с тесной взаимосвязью между последовательными уровнями значение d близко к нулю; это свидетельствует о том, что регулярная составляющая не полностью отражена в модели тренда, т. е. модель не адекватна реальному процессу. Если последовательные остатки независимы, то d близко к 2, и это свидетельствует о хорошем качестве модели. При отрицательной автокорреляции остатков (строго периодическом чередовании их знаков) d близко к 4. Заметим, что тест Дарбина – Уотсона, вообще говоря, не представляет собой статистический критерий в том смысле, что нельзя указать критическую область, которая позволяла бы отвергнуть гипотезу об отсутствии корреляции, если бы оказалось что в эту область попало наблюдаемое значение статистики d. Тест работает следующим образом. Если d – если – если – если Если Изобразим результат Дарбина –Уотсона в виде таблицы.
Совокупный критерий согласия Бокса – Пирса рассматривает совокупность первых k автокорреляций ряда остатков -
Статистика Q имеет c2 – распределение с k-m-1 степенями свободы. Пороговое значение для величины Q определяется по таблице. Нормальность ряда остатков проверяется с целью использовать это свойство в дальнейшем при построении доверительных интервалов прогноза. Ввиду малого числа наблюдений в большинстве временных рядов (меньше 30) это свойство может быть проверено лишь посредством вычисления оценок коэффициентов асимметрии
где S – средняя квадратичная ошибка
Для нормального распределения Гипотеза Н0 о нормальном распределении ряда остатков (
В этом случае доверительные интервалы для прогноза будут достаточно достоверными.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.59.242 (0.011 с.) |

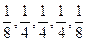 ].
].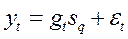 , (t = 1,…,n; q = 1,…,4), (4.49)
, (t = 1,…,n; q = 1,…,4), (4.49)
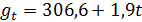 . (4.50)
. (4.50) .
.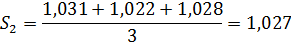 .
. .
.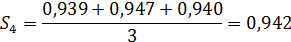 .
.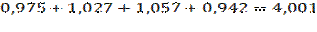
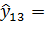 (306,6+1,9
(306,6+1,9 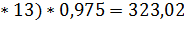 .
. (306,6+1,9
(306,6+1,9 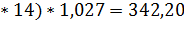 .
. (306,6+1,9
(306,6+1,9 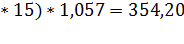 .
.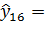 (306,6+1,9
(306,6+1,9  .
. удовлетворяет требованиям нулевого среднего, случайности, независимости последовательных значений и в ряде случаев нормальности.
удовлетворяет требованиям нулевого среднего, случайности, независимости последовательных значений и в ряде случаев нормальности.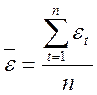 .
. близко к нулю, то можно считать, что модель не содержит систематической ошибки и адекватна по критерию нулевого среднего. Этот вопрос может быть решен со статистических позиций.
близко к нулю, то можно считать, что модель не содержит систематической ошибки и адекватна по критерию нулевого среднего. Этот вопрос может быть решен со статистических позиций. .
. ,
,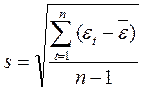 – среднее квадратичное отклонение остатков;
– среднее квадратичное отклонение остатков;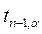 – табличное значение критерия Стьюдента с n-1 степенью свободы уровня значимости
– табличное значение критерия Стьюдента с n-1 степенью свободы уровня значимости  .
. . (4.51)
. (4.51) (4.52)
(4.52)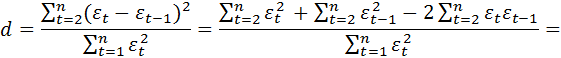

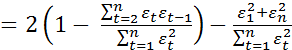 .
.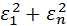 значительно меньше
значительно меньше  и
и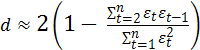 ,
,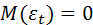
 .
.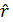 окажется не сильно отличающимся от нуля, а значение статистики d будет близко к двум.
окажется не сильно отличающимся от нуля, а значение статистики d будет близко к двум.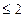 , то значение d сравниваетсяс табличными значениями dL и dU :
, то значение d сравниваетсяс табличными значениями dL и dU :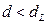 , то гипотеза о независимости
, то гипотеза о независимости 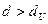 , то гипотеза о независимости
, то гипотеза о независимости  , то нет достаточных оснований для принятия решения.
, то нет достаточных оснований для принятия решения. , то с критическими значениями dL и dU, взятыми из таблиц, сравнивается не d, а 4- d и решение принимается по тем же правилам.
, то с критическими значениями dL и dU, взятыми из таблиц, сравнивается не d, а 4- d и решение принимается по тем же правилам.

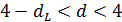
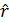 1 (e),
1 (e), 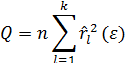 .
.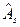 и эксцесса
и эксцесса  для ряда остатков
для ряда остатков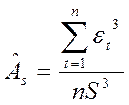 ;
;  ,
,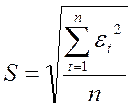 .
. и
и  .
.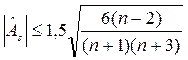 ;
;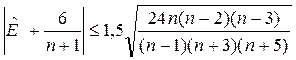 .
.


