
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о прогнозировании и прогностикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Богданов, А. И. Бог73 Эконометрика: учеб. пособие/ А. И. Богданов – СПб.: СПГУТД, 2010. – 104 с. ISBN 978-5-7937-0554-7
В учебном пособии рассмотрены теоретические аспекты математического моделирования и прогнозирования, вопросы построения, исследования и применения регрессионных моделей для прогнозирования экономических переменных, системы взаимосвязанных (одновременных) уравнений, математические модели стационарных и нестационарных временных рядов и их использование для прогнозирования. Учебное пособие предназначено для изучения студентами экономических специальностей дисциплины «Эконометрика». Его содержание полностью соответствует государственному образовательному стандарту по дисциплине «Эконометрика».
© ГОУ ВПО «СПГУТД», 2010 © Богданов А. И., 2010 ISBN 978-5-7937-0554-7 ВВЕДЕНИЕ
Эконометрика как научная дисциплина возникла в 30-х годах прошлого столетия. Появление эконометрики связано с широким проникновением математических и статистических методов в различные области науки: биологию, социологию, психологию. Математизация не смогла обойти и экономику. Кризис 1929–1933 гг. привел к критическому пересмотру методов анализа, применявшихся в экономике. В исследованиях начали учитывать случайные аспекты экономических явлений. Г. Тинтнер отождествляет эконометрику с экономической статистикой, Г. Хансен подразумевает под эконометрикой применение математических и статистических методов в экономике. Согласно некоторым другим определениям эконометрика есть синтез экономической теории, математики и статистики и поэтому часто ее называют также математической экономикой. Каждое из этих определений имеет свое рациональное звено. Объединяя все рациональные моменты указанных определений, можно считать, что эконометрика представляет собой дисциплину, задача которой состоит в измерении связей между экономическими величинами на основе статистических данных. Таким образом, эконометрика использует знания экономической теории, математики и экономической статистики. Язык экономики все больше становится языком математики, а экономику все чаще называют одной из наиболее математизированных наук. Достижения современной экономической науки предъявляют новые требования к высшему профессиональному образованию экономистов. Современное экономическое образование, утверждает директор ЦЭМИ РАН академик В. Л. Макаров, держится на трех китах – макроэкономике, микроэкономике и эконометрике. Если в период плановой экономики упор делался на балансовых и оптимизационных методах, построении оптимизационных моделей отраслей и предприятий, то в период рыночной экономики возрастает роль эконометрических методов. Без знания этих методов не возможно ни исследование и теоретическое обобщение эмпирических зависимостей экономических переменных, ни построение сколь-нибудь надежного прогноза в банковском деле, финансах или бизнесе.
1. ПОНЯТИЕ О ПРОГНОЗИРОВАНИИ И МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ Понятие о прогнозировании и прогностике
В литературе имеется большое количество терминов и определений, связанных с проблемой прогнозирования, которые, к сожалению, трактуются далеко не однозначно. К ним относятся такие термины, как предсказание (prediction), прогнозирование (forecasting), антиципация (anticipation) и некоторое обобщающее понятие предвидение (prognousis). Предсказание (prediction) представляет собой не вероятностное (практически достоверное) утверждение о будущем. Оно возможно на основании физических законов. Например, можно практически без ошибок рассчитать положение планет в обозримом будущем. Прогнозирование (forecasting) представляет собой вероятностное утверждение о будущем. Антиципация (anticipation) – логически сконструированная модель возможного будущего с неопределенным уровнем достоверности. При этом «будущее» представляется в виде событий, ситуаций и т. п. При этом предсказание, прогнозирование и антиципация являются частным случаем предвидения, которое в принципе представляет собой некоторое рассуждение о будущем. Результатом предвидения является прогноз будущего. Прогнозы по своему содержанию могут быть качественными и количественными. Качественные прогнозы могут быть получены как путем логических рассуждений, так и на основе количественных прогнозов процессов и явлений, оказывающих влияние на прогнозируемый процесс. Количественный прогноз связан с какими-то численными параметрами прогнозируемого объекта, которые, по сути, являются случайными величинами (при прогнозировании). Поэтому с ними связаны такие характеристики случайных величин, как математическое ожидание, дисперсия, наиболее вероятное значение и т. д. При количественном прогнозировании различают точечные и интервальные прогнозы. Под точечным прогнозом понимают оценку математического ожидания прогнозируемого параметра в заданный момент времени в будущем. Однако, как указывалось выше, мы никогда не сможем точно «угадать» будущую ситуацию. Поэтому значение точечного прогноза, как правило, не является достаточным и может рассматриваться как некоторый центр, около которого по некоторому закону будут группироваться будущие события. Поэтому дополнительно к точечному прогнозу рассматривается интервальный прогноз, характеризующий размер области, в которую с заданной вероятностью попадет будущее значение прогнозируемого параметра. Интервал наблюдения – отрезок времени, на котором имеются статистические данные о значении прогнозируемой величины до настоящего момента времени. Интервал упреждения – отрезок времени с момента осуществления прогноза до момента времени в будущем, для которого делается прогноз.
История развития прогностики как науки
Прогностика – наука о закономерностях разработки прогнозов, т. е., по сути, о методологии прогнозирования. Различные «размышления о будущем» появлялись на протяжении всей человеческой истории. К наиболее известным работам в этом направлении следует отнести работы Циолковского «Исследование мировых пространств реактивными приборами» (1926), «Будущее Земли и человечества» (1928) и т. д. В 1968 г. был создан Римский клуб, получивший свое название по месту нахождения штаб-квартиры. Он объединил около полусотни видных ученых, бизнесменов и общественных деятелей для регулярного обсуждения проблем, поднятых экологической и технологической «волной». Клуб располагал достаточными средствами, чтобы заказать специальные научные исследования по данной проблематике. В 1970 г. на очередном заседании клуба был обсужден доклад американского кибернетика Дж. Форрестера об опыте моделирования социальных систем с использованием ЭВМ, а в 1972 г. вышла его книга «Пределы роста», которая вызвала очередную сенсацию и сохранила актуальность до наших дней (по его прогнозам на протяжении первых десятилетий ХХI в. минеральные ресурсы окажутся исчерпанными и рост производства прекратится). В СССР в 1966 г. был поставлен вопрос о необходимости повышения научного уровня народнохозяйственного планирования и управления. Это привело к созданию первых секторов и отделов прогнозирования в ряде научно-исследовательских институтов. Были подготовлены первые специальные труды по методологии прогнозирования: Г. М. Добров «Прогнозирование науки и техники» (1969), В. Г. Гмошинский и Г. И. Флиорент «Теоретические основы инженерного прогнозирования» (1973), С. А. Саркисян и Л. В. Голованов «Прогнозирование развития больших систем (1975), А. Г. Ивахненко «Долгосрочное прогнозирование и управление сложными системами» (1975) и др. К числу первых учебников по прогнозированию относятся «Теория прогнозирования и принятия решений»/под ред. С. А. Саркисяна (1977) и «Рабочая книга по прогнозированию»/под ред. И. В. Бестужева-Лады (1982). С 70-х годов регулярно проводились семинары по теории и практике прогнозирования в Киеве, Ленинграде, Новосибирске.
Корреляционный анализ
В качестве меры тесноты связи между двумя случайными величинами обычно используется коэффициент корреляции r
где
При этом Выборочный коэффициент корреляции
где
n – число наблюдений (объем выборки). На практике используются следующие формулы для «ручных» вычислений:
Если в системе имеется несколько переменных, которые коррелируют друг с другом, то на значение коэффициента корреляции между двумя переменными сказывается влияние других переменных. В связи с этим возникает необходимость исследовать частную корреляцию между переменными при исключении влияния остальных переменных системы. Частный коэффициент корреляции – это мера линейной зависимости между двумя случайными величинами из некоторой совокупности случайных величин X1, X2, …,Xk, когда исключено влияние всех остальных величин. Частный коэффициент корреляции выражается через элементы корреляционной матрицы
где Rij – алгебраическое дополнение элемента rij в корреляционной матрице. Если случайные величины попарно не коррелированны, т. е. В этом легко убедиться, рассмотрев матрицу R, представляющую из себя в этом случае единичную матрицу
R =
Выборочную оценку коэффициента частной корреляции можно получить следующим образом
где При системе из трех случайных величин из общей формулы (2.5) следует, что
Сравнивая выборочные обычный и частный коэффициенты корреляции, можно делать вывод о том, насколько взаимосвязь между Xi и Xj обусловлена их зависимостью от других случайных величин. Пример. В Англии исследовали влияние погоды на урожай. При этом рассматривали три переменные:
Корреляционная матрица, полученная по данным за 20 лет, имела вид
Отрицательная зависимость между урожаем сена ( Рассчитаем значение частного коэффициента корреляции между
При этом
Таким образом,
и связь не является отрицательной.
Корреляционное отношение
Для измерения тесноты связи между двумя случайными величинами используется не только коэффициент корреляции, но и корреляционное отношение. Рассмотрим аналитическую группировку. Имеет место следующее соотношение
где
Внутригрупповая дисперсия характеризует ту часть дисперсии признака-результата, которая не зависит от признака-фактора. Ее оценка определяется по формуле
где (i- й) группы по признаку-фактору; ni – численность i- й группы; k – количество групп; n – общий объем выборки. Межгрупповая дисперсия отражает ту часть общей дисперсии признака-результата, которая объясняется влиянием признака-фактора. Ее оценка определяется по формуле
где
Коэффициент детерминации определяет долю объясненной дисперсии в общей дисперсии признака-результата:
Корреляционное отношение определяется как
В литературе по эконометрике корреляционное отношение принято называть индексом корреляции. Оно является мерой тесноты связи при любой форме зависимости, а не только линейной, как коэффициент корреляции.
Парная линейная регрессия
Следующий этап исследования корреляционной связи заключается в том, чтобы описать зависимость признака-результата от признака-фактора некоторым аналитическим выражением.
где ε – случайная компонента. Модель парной линейной регрессии может быть записана и в следующем виде:
где xi – значение переменной X в i -м наблюдении; yi – значение переменной Y в i -м наблюдении; εi – значение случайной компоненты ε в i -м наблюдении; n – число наблюдений (объем выборки). Основные предположения регрессионного анализа относятся к случайной компоненте В классической модели регрессионного анализа имеют место следующие предположения: 1. Величины 2. Математическое ожидание случайной компоненты ( 3.Случайные величины 4. Случайные компоненты Эти четыре предположения являются необходимыми для проведения регрессионного анализа в рамках классической модели. Пятое предположение дает достаточные условия для обоснованного проведения проверки статистической значимости полученных регрессий и заключается в нормальности закона распределения В общем случае задача оценки параметров регрессии может решаться с помощью метода наименьших квадратов (МНК). Рассмотрим использование метода наименьших квадратов для оценки параметров регрессии
На практике имеется серия наблюдений (xi;yi) (i=1,..,n). При этом
Тогда
Возьмем частные производные Q по параметрам
Пример Исследуем зависимость розничного товарооборота магазинов (млрд р.) от среднесписочного числа работников. Обозначим: x – число работников; y – товарооборот.
Исходные данные и результаты расчетов приведены в таблице.
Вычислим выборочный коэффициент корреляции:
Тогда
Проверим значимость выборочного коэффициента корреляции. Для этого вычислим статистику t:
Табличное значение критерия Стьюдента для
Так как 15,65 > 2,45, то полученный коэффициент корреляции статистически значим. Найдем коэффициенты парной линейной регрессии:
и регрессия имеет вид
Прогнозное значение розничного товарооборота при
Регрессионных моделей
Ранее нами была изучена классическая линейная модель множественной регрессии. Однако мы не касались некоторых проблем, связанных с практическим использованием модели множественной регрессии. К их числу относится мультиколлинеарность. Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных. Мультиколлинеарность может проявляться в функциональной и стохастической формах. При функциональной форме мультиколлинеарности по крайней мере одна из парных связей между объясняющими переменными является линейной функциональной зависимостью. В этом случае матрица ХTX особенная, так как содержит линейно зависимые векторы-столбцы и ее определитель равен нулю. Это приводит к невозможности решения соответствующей системы уравнений и получения оценок параметров регрессионной модели. Однако в экономических исследованиях мультиколлинеарность чаще всего проявляется в стохастической форме, когда между хотя бы двумя объясняющими переменными существует тесная корреляционная связь. Матрица ХTX в этом случае является неособенной, но ее определитель очень мал. В результате получаются значительные дисперсии оценок коэффициентов регрессии Наличие мультиколлинеарности системы объясняющих переменных можно статистически проверить по тесту Глобера – Феррара. При отсутствии мультиколлинеарности статистика
где
det Вычисленное значение Одним из методов снижения мультиколлинеарности системы объясняющих переменных X1, X2, …, Xk является выявление пар переменных с высокими коэффициентами корреляции (более 0,8). При этом одну из таких переменных исключают из рассмотрения. Какую из двух переменных удалить решают на основании экономических соображений или оставляют ту, которая имеет более высокий коэффициент корреляции с зависимой переменной. Полезно также находить множественные коэффициенты корреляции между одной объясняющей переменной и некоторой группой из них. Множественный коэффициент корреляции служит мерой линейной зависимости между случайной величиной Хi и некоторым набором других случайных величин X1, X2, X3, …,Xi-1,Xi+1,… Xk. Множественный коэффициент корреляции Чем ближе значения коэффициента множественной корреляции к единице, тем лучше приближение случайной величины Хi линейной комбинацией случайных величин X1, X2, X3, …,Xi-1,Xi+1,… Xk. Множественный коэффициент корреляции выражается через элементы корреляционной матрицы следующим образом:
где │R│– определитель корреляционной матрицы R; Rii – алгебраическое дополнение элемента rii. Если С другой стороны, В качестве выборочной оценки коэффициента множественной корреляции используется выражение
Наличие высокого множественного коэффициента корреляции (более 0,8) также свидетельствует о мультиколлинеарности. Еще одним из методов уменьшения мультиколлинеарности является использование пошаговых процедур отбора наиболее информативных переменных с использованием скорректированного коэффициента детерминации. Недостатком коэффициента детерминации R2 для выбора наилучшего уравнения регрессии является то, что он всегда увеличивается при добавлении новых переменных в регрессионную модель. Поэтому целесообразно использовать скорректированный коэффициент детерминации
В отличие от R2 скорректированный коэффициент На первом шаге рассматривается лишь одна объясняющая переменная, имеющая с зависимой переменной Y наибольший коэффициент корреляции (детерминации). На втором шаге включается в регрессию новая объясняющая переменная, которая вместе с первоначальной дает наиболее высокий скорректированный коэффициент детерминации с Y ит. д. Процедура введения новых переменных продолжается до тех пор, пока будет увеличиваться скорректированный коэффициент детерминации
Пример. Необходимо исследовать зависимость между результатами письменных вступительных и курсовых экзаменов по математике. Получены следующие данные о числе решенных задач на вступительных экзаменах X (задание – 10 задач) и курсовых экзаменах Y (задание – 7 задач) 12 студентов, а также распределение этих студентов по фактору «пол».
Построим линейную регрессионную модель Y по X с использованием фиктивной переменной по фактору «пол». Для ее учета введем в регрессионную модель фиктивную бинарную переменную Z.
1, если i -й студент мужского пола; zi = 0, если i -й студент женского пола.
Таким образом, мы получили регрессионную модель
с общей матрицей
│1 1 1 1 1 1 1 1 1 1 1 1 │ ХT = │10 6 8 8 6 7 6 7 9 6 5 7 │ │1 0 1 0 0 1 0 1 1 0 1 0 │
По формуле (2.45) найдем вектор оценок параметров регрессии
Таким образом, выборочное уравнение множественной регрессии примет вид
Коэффициент детерминации Уравнение регрессии значимо по F -критерию при 5%-м уровне значимости, так как в соответствии с (2.55)
Из (2.64) следует, что при том же числе решенных задач на вступительных экзаменах Х, на курсовых экзаменах юноши решают в среднем на 0,466 ≈ 0,5 задачи больше. Полученное уравнение множественной регрессии значимо по
Следовательно, по имеющимся данным влияние фактора «пол» оказалось несущественным, и у нас есть основание считать, что регрессионная модель результатов курсовых экзаменов по математике в зависимости от вступительных одна и та же для юношей и девушек.
Нелинейные модели регрессии
До сих пор мы рассматривали линейные регрессионные модели, в которых переменные имели первую степень (модели, линейные по переменным), а параметры выступали в виде коэффициентов при этих переменных (модели, линейные по параметрам). Однако соотношения между экономическими переменными далеко не всегда можно выразить линейными функциями. Так, например, нелинейными оказываются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства – трудом и капиталом). Для оценки параметров нелинейных моделей используются два подхода. Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными. Второй подход применяется в случае, когда подобрать соответствующее линеаризующее преобразование не удается. В этом случае применяются методы нелинейной оптимизации на основе исходных переменных. Для линеаризации модели в рамках первого подхода могут использоваться как модели, не линейные по переменным, так и не линейные по параметрам. Если модель нелинейна по переменным, то введением новых переменных ее можно свести к линейной модели, для оценки параметров которой использовать обычный метод наименьших квадратов. Так, например, если необходимо оценить параметры регрессионной модели
то, вводя новые переменные
параметры которой находятся обычным методом наименьших квадратов. Более сложной проблемой является нелинейность модели по параметрам, так как непосредственное применение метода наименьших квадратов для их оценивания невозможно. К числу таких моделей можно отнести, например, мультипликативную модель
экспоненциальную модель
и другие. В ряде случаев путем подходящих преобразований эти модели удается привести к линейной форме. Так, модели (2.65) и (2.66) могут быть приведены к линейным логарифмированием обеих частей уравнений. Тогда, например, модель (2.65) примет вид
К модели (2.67) уже можно применять обычные методы исследования линейной регрессии. Следует однако отметить и недостаток такой замены, связанный с тем, что вектор оценок Заметим попутно, что к модели
изложенные методы уже непригодны, так как модель (2.68) нельзя привести к линейному виду. В качестве примера использования линеаризирующего преобразования регрессии рассмотрим производственную функцию Кобба – Дугласа
где Учитывая влияние случайных возмущений, присущих каждому экономическому явлению, функцию Кобба–Дугласа (2.69) можно представить в виде
Полученную мультипликативную модель легко свести к линейной путем логарифмирования обеих частей уравнения (2.70). Тогда для i -го наблюдения получим
Задание 1 В табл. 1 приведены 5 показателей деятельности торговых предприятий. В соответствии с таблицей выберите номера 2-х показателей.
Т а б л и ц а 1 Показатели деятельности торговых предприятий
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 858; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.017 с.) |

 , (2.1)
, (2.1) – ковариация случайных величин X и Y;
– ковариация случайных величин X и Y; – среднее квадратичное отклонение случайной величины X;
– среднее квадратичное отклонение случайной величины X; – среднее квадратичное отклонение случайной величины Y;
– среднее квадратичное отклонение случайной величины Y; – математическое ожидание случайной величины X;
– математическое ожидание случайной величины X; – математическое ожидание случайной величины Y;
– математическое ожидание случайной величины Y; – математическое ожидание XY.
– математическое ожидание XY.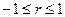 . При
. При  связь становится функциональной.
связь становится функциональной.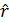 рассчитывается по формуле
рассчитывается по формуле , (2.2)
, (2.2) – значение случайной величины X для i -го наблюдения (объекта);
– значение случайной величины X для i -го наблюдения (объекта);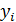 – значение случайной величины Y для i -го наблюдения (объекта);
– значение случайной величины Y для i -го наблюдения (объекта); ,
,  – выборочные средние значения случайных величин X и Y;
– выборочные средние значения случайных величин X и Y; ;
; ; (2.3)
; (2.3) .
. , составленной из коэффициентов парной корреляции.
, составленной из коэффициентов парной корреляции. , (2.4)
, (2.4) при
при  , то и все частные коэффициенты корреляции равны нулю.
, то и все частные коэффициенты корреляции равны нулю.
 , (2.5)
, (2.5) - алгебраическое дополнение элемента
- алгебраическое дополнение элемента  в выборочной корреляционной матрице
в выборочной корреляционной матрице  .
. (2.6)
(2.6) – урожай сена;
– урожай сена; – количество осадков;
– количество осадков; количество дней с высокой температурой.
количество дней с высокой температурой.

 ) (
) ( представляется весьма странной.
представляется весьма странной. .
. = (-1)4
= (-1)4  = - 0,048;
= - 0,048; =(-1)2
=(-1)2  = 0,6864;
= 0,6864;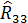 = (-1)6
= (-1)6  =0,36.
=0,36.
 , (2.8)
, (2.8) − полная дисперсия признака-результата;
− полная дисперсия признака-результата; − внутригрупповая дисперсия;
− внутригрупповая дисперсия; − межгрупповая дисперсия.
− межгрупповая дисперсия. , (2.9)
, (2.9) – оценка дисперсии признака-результата в пределах отдельной
– оценка дисперсии признака-результата в пределах отдельной , (2.10)
, (2.10) − групповое среднее i -й группы;
− групповое среднее i -й группы; – общее среднее значение признака-результата.
– общее среднее значение признака-результата. . (2.11)
. (2.11) . (2.12)
. (2.12) ;
;  ,
, − средний уровень показателя Y при данном значении x;
− средний уровень показателя Y при данном значении x;
 и имеют решающее значение для правильного и обоснованного применения регрессионного анализа на практике.
и имеют решающее значение для правильного и обоснованного применения регрессионного анализа на практике.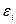 (а также зависимые переменные
(а также зависимые переменные  являются случайными, а объясняющая переменная
являются случайными, а объясняющая переменная 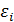 равно нулю
равно нулю ).
). ). Данное условие называется условием гомоскедастичности.
). Данное условие называется условием гомоскедастичности. являются некоррелированными между собой (
являются некоррелированными между собой ( при
при  .
. .
. . (2.14)
. (2.14)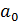 и
и  и приравняем их нулю:
и приравняем их нулю:
 , (2.15)
, (2.15) .
.




 ;
; 
 ;
;  ;
; ;
; 
 ;
;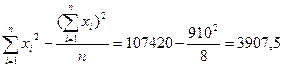 ;
; .
.

 = n -2 = 6 и
= n -2 = 6 и 

 ;
;
 .
. составит
составит

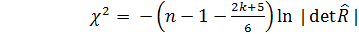 , (2.58)
, (2.58)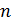 – объем выборки;
– объем выборки;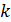 – количество объясняющих переменных;
– количество объясняющих переменных;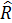 – определитель выборочной корреляционной матрицы объясняющих переменных
– определитель выборочной корреляционной матрицы объясняющих переменных 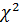 – распределение с k(k-1)/2 степенями свободы.
– распределение с k(k-1)/2 степенями свободы.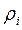 определяется как обычный коэффициент парной корреляции между Хi и Хi*, где Хi* − наилучшее линейное приближение Хi случайными величинами X1, X2, X3, …,Xi-1,Xi+1,… Xk.
определяется как обычный коэффициент парной корреляции между Хi и Хi*, где Хi* − наилучшее линейное приближение Хi случайными величинами X1, X2, X3, …,Xi-1,Xi+1,… Xk.
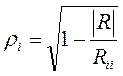 , (2.59)
, (2.59) , то величина Хi представляет собой линейную комбинацию случайных величин X1, X2, X3, …,Xi-1,Xi+1,… Xk.
, то величина Хi представляет собой линейную комбинацию случайных величин X1, X2, X3, …,Xi-1,Xi+1,… Xk. только тогда, когда Хi не коррелированна ни с одной из случайных величин X1, X2, X3, …,Xi-1,Xi+1,… Xk.
только тогда, когда Хi не коррелированна ни с одной из случайных величин X1, X2, X3, …,Xi-1,Xi+1,… Xk.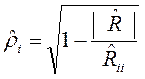 . (2.60)
. (2.60) , определяемый по формуле
, определяемый по формуле .
.

 .
. . (2.64)
. (2.64) .
. .
. – критерию. Однако коэффициент регрессии β1 при фиктивной переменной Z незначим по t - критерию
– критерию. Однако коэффициент регрессии β1 при фиктивной переменной Z незначим по t - критерию .
. (i=1,…,n),
(i=1,…,n), , получим линейную модель
, получим линейную модель (i=1,…,n),
(i=1,…,n), (i=1,..,n), (2.65)
(i=1,..,n), (2.65) (i=1,..,n) (2.66)
(i=1,..,n) (2.66) (i=1,..,n). (2.67)
(i=1,..,n). (2.67)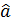 получается не из условия минимизации суммы квадратов отклонений для исходных переменных, а из условия минимизации суммы квадратов отклонений для преобразованных переменных, что не одно и то же. Следует также подчеркнуть, что критерии значимости и интервальные оценки параметров, применимые для нормальной линейной регрессии, требуют, чтобы нормальный закон распределения в моделях (2.65), (2.66) имел логарифм вектора возмущений
получается не из условия минимизации суммы квадратов отклонений для исходных переменных, а из условия минимизации суммы квадратов отклонений для преобразованных переменных, что не одно и то же. Следует также подчеркнуть, что критерии значимости и интервальные оценки параметров, применимые для нормальной линейной регрессии, требуют, чтобы нормальный закон распределения в моделях (2.65), (2.66) имел логарифм вектора возмущений  а вовсе не ε.
а вовсе не ε. (i=1,..,n) (2.68)
(i=1,..,n) (2.68) , (2.69)
, (2.69) – объем производства;
– объем производства; 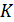 – затраты капитала;
– затраты капитала;  – затраты труда.
– затраты труда. . (2.70)
. (2.70) =
=  +
+  (i=1,..,n). (2.71)
(i=1,..,n). (2.71)


