
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тест Гольдфельда–Квандта на гомоскедастичностьСодержание книги
Поиск на нашем сайте
Этот тест применяется в том случае, если ошибки регрессии можно считать нормально распределенными случайными величинами. Предположим, что средние квадратичные отклонения возмущений Упорядочим n наблюдений в порядке возрастания значений Х и выберем m первых и m последних наблюдений. В этом случае гипотеза о гомоскедастичности будет равносильна тому, что значения Гипотеза о равенстве дисперсий двух нормально распределенных совокупностей проверяется с помощью критерия Фишера. Нулевая гипотеза о равенстве дисперсий двух наборов по m наблюдений, то есть гипотеза о гомоскедастичности отвергается, если
где k – число независимых переменных модели. Мощность теста, т. е. вероятность отвергнуть гипотезу о гомоскедастичности, когда действительно гомоскедастичности нет, оказывается максимальной, если выбирать m порядка n/3.
Пример. По данным n =150 наблюдений о доходе индивидуума Y, уровне его образования X1 и возрасте X2 выяснить, можно ли считать на уровне значимости α = 0,05 линейную регрессионную модель Y по X1 и X2 гомоскедастичной.
Возьмем по m = n/3=150/3=50 значений доходов лиц с наименьшим и наибольшим уровнем образования X1.
Вычислим суммы квадратов остатков
По таблице распределения Фишера находим, что
Это означает, что гипотеза о гомоскедастичности должна быть отвергнута.
Задание 1 В табл. 1 приведены 5 показателей деятельности торговых предприятий. В соответствии с таблицей выберите номера 2-х показателей.
Т а б л и ц а 1 Показатели деятельности торговых предприятий за год
С помощью корреляционного и регрессионного анализа изучить связь между показателями, указанными в Вашем варианте.
1. Рассчитать значение коэффициента корреляции для данных табл. 1. 2. Проверить статистическую значимость коэффициента корреляции. 3. Сделать вывод о тесноте статистической связи. 4. Найти коэффициенты парной линейной регрессии. 5. Проверить статистическую значимость уравнения регрессии по критерию Фишера. 6. Проверить статистическую значимость параметра 7. Сделать прогноз признака-результата, если признак-фактор принимает свое среднее значение.
СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ Системы независимых и взаимосвязанных (совместных) уравнений Сложные экономические процессы описываются с помощью системы взаимосвязанных (одновременных) уравнений. Различают несколько видов систем уравнений. 1. Система независимых уравнений, когда каждая зависимая переменная Yi (i=1,…,n) рассматривается как функция одного и того же набора факторов Xj (j=1,…,m):
………..
Для нахождения параметров этих моделей используется метод наименьших квадратов. 2. Система совместных (взаимозависимых) уравнений, когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую:
Переменные, определяемые внутри системы Yi (i=1,…,n), называются эндогенными, а переменные, определяемые вне системы Xj (j=1,…,m), – экзогенными. Кроме экзогенных переменных в системе могут быть эндогенные переменные, относящиеся к предыдущим моментам времени (эндогенные переменные с временным лагом). Экзогенные переменные и эндогенные переменные с временным лагом называются предопределенными переменными, так как значения этих переменных известны к текущему моменту времени. Пример Рассмотрим систему одновременных уравнений
где y1 – спрос-предложение; y2 – цена; х1 – уровень доходов. В рассматриваемой модели цена и спрос-предложение рассматриваются как эндогенные переменные, а доход – как экзогенная переменная. Предполагается, что экзогенные переменные определяются вне системы и поэтому не коррелируют со случайными компонентами, отражающим влияние неучтенных факторов. Эндогенные переменные, определяемые из уравнений системы, имеют ненулевую корреляцию со случайными компонентами. Действительно, разрешая уравнения относительно эндогенных переменных, получим
Отсюда
Нетрудно убедиться, что Таким образом, нарушаются основные предположения регрессионного анализа, что приводит к потере свойств оценок, получаемых методом наименьших квадратов (появляется смещенность и исчезает состоятельность оценок). Поэтому непосредственное применение метода наименьших квадратов приводит к грубым ошибкам.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 908; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.59.242 (0.01 с.) |

 пропорциональны значениям объясняющей переменной Х (это означает постоянство часто встречающегося на практике относительного, а не абсолютного, как в классической модели, разброса возмущений
пропорциональны значениям объясняющей переменной Х (это означает постоянство часто встречающегося на практике относительного, а не абсолютного, как в классической модели, разброса возмущений 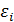 регрессионной модели).
регрессионной модели).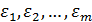 и
и  ,
,  , т. е. остатки
, т. е. остатки  , (2.77)
, (2.77) =
=  .
. .
. 1.
1.
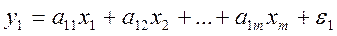



 ;
; ; …………
; ………… ;
;
 , (3.1)
, (3.1)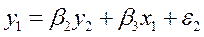 ,
,
 ,
, .
.
 ,
,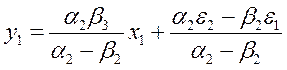 . (3.2)
. (3.2) и
и 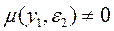 .
.


