
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка значимости уравнения регрессииСодержание книги
Поиск на нашем сайте Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. В математической статистике дисперсионный анализ рассмотрен как самостоятельный метод статистического анализа. Здесь же он применяется как вспомогательное средство для изучения качества регрессионной модели. Обозначим
или
где Q – общая сумма квадратов отклонений зависимой переменной от средней, а QR и Qe – соответственно сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов. Убедимся в том, что пропущенное в (2.38) третье слагаемое
Теперь
Схема дисперсионного анализа имеет вид, представленный в табл. 2.1.
Т а б л и ц а 2. 1. Схема дисперсионного анализа
Средние квадраты При отсутствии линейной зависимости между зависимой и объясняющими переменными случайные величины
где В случае линейной парной регрессии m=2, и уравнение регрессии значимо на уровне
Мерой качества регрессионной модели, характеристикой прогностической силы регрессионной модели является коэффициент детерминации, определяемый по формуле
Величина R2 показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной. Так как Чем ближе Средняя ошибка аппроксимации Еще одним показателем качества построенной регрессионной зависимости является средняя ошибка аппроксимации, которая вычисляется по формуле
Эта величина представляет собой среднюю относительную ошибку.
Пример Исследуем зависимость розничного товарооборота магазинов (млрд р.) от среднесписочного числа работников. Обозначим: x – число работников; y – товарооборот.
Исходные данные и результаты расчетов приведены в таблице.
Вычислим выборочный коэффициент корреляции:
Тогда
Проверим значимость выборочного коэффициента корреляции. Для этого вычислим статистику t:
Табличное значение критерия Стьюдента для
Так как 15,65 > 2,45, то полученный коэффициент корреляции статистически значим. Найдем коэффициенты парной линейной регрессии:
и регрессия имеет вид
Прогнозное значение розничного товарооборота при
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.009 с.) |

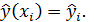 Согласно основной идее дисперсионного анализа
Согласно основной идее дисперсионного анализа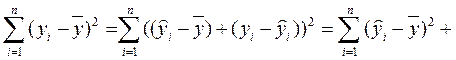
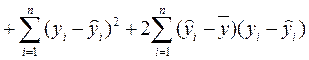 (2.37)
(2.37)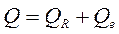 , (2.38)
, (2.38)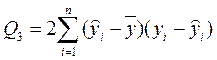 равно 0. Учитывая (2.30), (2.23), имеем
равно 0. Учитывая (2.30), (2.23), имеем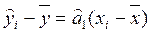 ,
,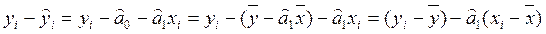 .
.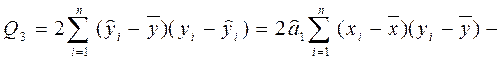
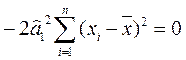 (с учетом соотношения (2.22).
(с учетом соотношения (2.22).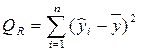
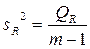
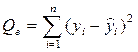
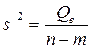
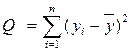
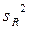 и
и  представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессией или объясняющей переменной Х ивоздействием неучтенных случайных факторов и ошибок; m – число оцениваемых параметров уравнения регрессии; n – число наблюдений.
представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессией или объясняющей переменной Х ивоздействием неучтенных случайных факторов и ошибок; m – число оцениваемых параметров уравнения регрессии; n – число наблюдений.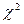 - распределение соответственно с m-1 и n-m степенями свободы, а их отношение – F - распределение с теми же степенями свободы. Поэтому уравнение регрессии значимо на уровне
- распределение соответственно с m-1 и n-m степенями свободы, а их отношение – F - распределение с теми же степенями свободы. Поэтому уравнение регрессии значимо на уровне  , если фактически наблюдаемое значение статистики
, если фактически наблюдаемое значение статистики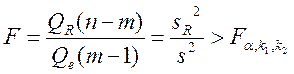 , (2.39)
, (2.39)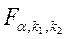 – табличное значение критерия Фишера, определенное на уровне значимости
– табличное значение критерия Фишера, определенное на уровне значимости 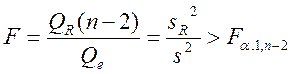 . (2.40)
. (2.40)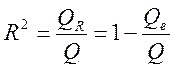 . (2.41)
. (2.41) , то
, то 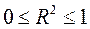 .
.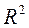 к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линейной регрессии. Если
к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линейной регрессии. Если 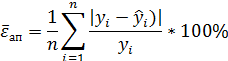 .
.




 ;
; 
 ;
;  ;
; ;
; 
 ;
;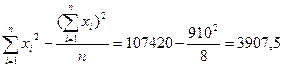 ;
; .
.

 = n -2 = 6 и
= n -2 = 6 и 

 ;
;
 .
. составит
составит



