
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Прогнозирование в рыночной экономикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель занятия: Приобретение теоретических знаний по методологии прогнозирования в рыночной экономике, а также формирование практических навыков по реализации процесса прогнозирования на макроуровне.
Вопросы к практическому занятию: 1. Содержание прогнозирования экономических объектов. 2. Источники прогнозно-аналитической информации. Требования к используемой информационной базе. 3. Инструменты предпрогнозных исследований. 4. Методы построения прогнозов. 5. Верификация и синтез экономических прогнозов.
Задания, вынесенные на практическое занятие: 1. Экспресс-опрос по пройденной теме. Промежуточное тестирование. 2. Практические задания. 2.1. Постройте структурно-логическую схему взаимосвязи прогнозирования с другими областями научного знания, исходя из места и роли прогнозирования в процессе управления. 2.2. Сформулируйте задачи прогнозирования развития конкретного экономического объекта (по вашему выбору). 2.3. Представьте, что вам необходимо подготовить исходную информацию для разработки прогноза производства продукции в Самарском регионе. Из приведенной ниже совокупности показателей необходимо выбрать: показатели для описания объекта прогнозирования, показатели для описания прогнозного фона, избыточную информацию. Исходная информация: - розничный товарооборот; - дефлятор ВВП; - товарные запасы в розничной торговле; - индекс потребительских цен; - официальный рыночный курс рубля к иностранной валюте; - ставки налогов; - производство товаров и услуг на душу населения; - уровень безработицы; - накопление сбережений во вкладах и ценных бумагах; - протяженность сети автомобильных дорог; - расходы на охрану окружающей среды; - объем промышленного производства Самарского региона в разрезе отраслей; - индекс оптовых цен промышленности; - динамика промышленного производства Самарского региона в разрезе отраслей; - численность занятых по отраслям; - производительность труда в разрезе отраслей; - стоимость основных производственных фондов; - инвестиции в основной капитал в разрезе отраслей. 3. Решение задач по теме. 3.1. По статистическим данным изучите зависимость оборота розничной торговли от ряда факторов. В табл. 3.1 представлены следующие данные: Y – оборот розничной торговли, млрд. руб.; Х (вариант 1) – денежные доходы населения, млрд. руб.; Х (вариант 2) – денежные расходы на покупку товаров и услуг, млрд. руб.; Х (вариант 3) – численность безработных, тыс. чел.
Таблица 3.1 Исходные данные
А) Для заданного набора данных постройте модель регрессии. Оцените точность и адекватность построенного уравнения регрессии. Б) Дайте экономическую интерпретацию параметров модели. В) Рассчитайте прогнозные значения результативного показателя в зависимости от средних темпов прироста факторных показателей. Г) Проведите аналогичный расчет на материалах Самарского региона РФ. 3.2. В табл. 3.2 представлен временной ряд некоторого показателя. На основе показателей ряда необходимо получить точечные интервальные прогнозы на двухлетний период упреждения. Таблица 3.2 Информация о периоде наблюдения
3.3. Рассчитайте по данным табл. 3.3 параметры уравнения тренда и показатели адекватности функции реальным условиям. Является ли исследуемая тенденция устойчивой? Таблица 3.3 Временной ряд спроса на продукт
3.4. Используя данные табл. 3.4, рассчитайте прогноз инвестиций в основной капитал предприятий региона на 2013 год методом экспоненциального сглаживания.
Таблица 3.4 Объем инвестиций в основной капитал предприятий региона
3.5. Проводится экспертная оценка по прогнозированию валового сбора зерновых культур в Самарской области. В табл. 3.5 приведены результаты третьего тура по методу Дельфи. На основе статистической характеристики ответов экспертов сделайте вывод о степени согласованности мнений и возможности завершения экспертизы. В случае положительного результата приведите прогнозное значение валового сбора зерновых культур. Таблица 3.5 Ранжированный ряд экспертных оценок
3.6. Определите прогнозное значение производства продукции на восьмой год методом экстраполяции тренда по данным табл. 3.6. Таблица 3.6 Динамика производства продукции
3.7. Оцените правильность построения временного ряда (табл. 3.7), исправьте допущенные ошибки. Таблица 3.7 Исходные данные
3.8. Проанализируйте зависимость вида тренда от периода ретроспекции. Внимательно посмотрите на информацию, представленную ниже. Она характеризует один и тот же объект исследования. Обратите внимание, чем отличаются данные первого и второго вариантов (табл. 3.8 и 3.9). Постройте график временного ряда, используя исходные данные первого варианта, проведите сглаживание временного ряда и на основе визуального анализа выберите форму кривой, наиболее точно описывающей анализируемый процесс. Таблица 3.8 Первый вариант. Объем выпуска продукции, млн. руб.
Повторите все расчеты для второго варианта исходных данных. Сделайте выводы. Таблица 3.9 Второй вариант. Объем выпуска продукции, млн. руб.
3.9. Проанализируйте зависимость вида тренда от размера временных интервалов. Изучите исходные данные по первому и второму варианту (табл. 3.10 и 3.11), они характеризуют один и тот же объект исследования за один и тот же период времени. Постройте график временного ряда для первого варианта, проведите предварительную обработку информации и выберите форму кривой, наиболее точно описывающую исследуемый процесс. Таблица 3.10 Первый вариант. Объем продаж безалкогольных напитков, млн. руб.
Повторите все процедуры для второго варианта и сделайте вывод по заданию в целом. Таблица 3.11 Второй вариант. Объем продаж безалкогольных напитков, млн. руб.
3.10. Эксперты оценили важность параметров, учитываемых потребителями туристических услуг Самарского региона (табл. 3.12). Переведите коэффициенты весомости в ранги, используемые при составлении прогноза методом ранговой корреляции, оцените степень согласованности мнений экспертов. Таблица 3.12 Коэффициенты весомости параметров
3.11. Прогнозная оценка затрат на создание новой продукции была получена методом Дельфи. Опрос проводился в два тура. Проведите статистическую обработку информации, полученной в первом и втором турах экспертного опроса (табл. 3.13). Сделайте выводы. Таблица 3.13 Результаты экспертного опроса
3.12. На основе данных о производстве молока в 2010 - 2012 гг. (табл. 3.14) составьте прогноз производства молока в 2013 году. Таблица 3.14 Производства молока в хозяйствах всех категорий, тыс. т
3.13. На основе статистических данных о средних ценах производителей топливно-энергетических ресурсов оцените степень влияния цены на нефть на цены бензина автомобильного. Сделайте вывод о возможности использования прогноза цены нефти для разработки прогнозов цен на бензин автомобильный. При обнаружении зависимости рассчитайте прогнозные значения цен на названные топливно-энергетические ресурсы при условии, что в прогнозном периоде цена нефти составит 10000 руб. за тонну (табл. 3.15). Таблица 3.15 Средние цены производителей топливно-энергетических ресурсов, руб. / т
3.14. По данным, представленным в табл. 3.16, изучите зависимость валового национального дохода от инвестиций (все данные в трлн. руб.).
Таблица 3.16 Исходные данные
А) Для заданного набора данных постройте модель регрессии. Оцените точность и адекватность построенного уравнения регрессии. Дайте экономическую интерпретацию параметров модели. Б) Получите прогнозные значения валового национального дохода при сохранении средних темпов роста инвестиций. В) Используя статистические данные, проведите аналогичные расчеты для РФ за период 2000 – 2011 гг. 4. Подготовка рефератов по следующей тематике: 4.1. Имитационное моделирование в прогнозировании. 4.2. Морфологический анализ как метод оценки качественно различных альтернатив. 4.3. Прогнозные сценарии в экономическом прогнозировании. 4.4. Роль прогнозирования в принятии управленческих решений. 4.5. Особенности моделей авторегрессии. 4.6. Многофакторные модели прогнозирования. 4.7. Метод построения прогнозного сценария. 4.8. Системно-структурные методы прогнозирования. 4.9. Теория предвидения Н. Д. Кондратьева и методология интегрального прогнозирования. 4.10. Прогнозирование циклов и кризисов. 4.11. Глобальный срез долгосрочного прогнозирования. 5. Докажите или опровергните следующее утверждение «Будущим нельзя управлять. Его можно лишь предвидеть и подстраиваться под него». (Эссе). 6. Подготовка конспекта теоретического вопроса по пройденной теме.
Методические указания
Сравнение уровней ряда динамики производится двумя способами: цепным и базисным. При цепном способе каждый уровень Для определения относительной скорости роста применяют коэффициент роста Кр, который определяется как отношение значений данного уровня
Коэффициент роста показывает, во сколько раз данный уровень больше цепного или базисного или какую часть от них составляет рассматриваемый уровень. Коэффициент роста, выраженный в процентах, определяет темп роста:
Тогда цепные и базисные формулы расчета темпов роста выглядят следующим образом:
Изменение величины абсолютного прироста уровней ряда динамики определяется темпом прироста Тпр, который рассчитывается так:
С помощью темпов прироста можно узнать, на сколько процентов увеличился (снизился) данный уровень по сравнению с цепным или базисным. Расчет темпов прироста можно вести по упрощенной формуле: Тпр = (Кр – 1)х100 или Тпр = Тр – 100. (3.4) Показатель абсолютного значения 1% прироста
Его расчет имеет экономический смысл только на цепной основе. Абсолютное значение 1% прироста можно рассчитать иначе:
На основе рассчитанных показателей строится график динамических показателей. Среднее значение Среднее значение интервального ряда динамики с равностоящими уровнями вычисляется по формуле средней арифметической простой:
где п – число уровней. Среднее значение интервального ряда динамики с неравностояшими уровнями рассчитывается по формуле средней арифметической взвешенной:
где Средний уровень
Средняя хронологическая для ряда с неравностоящими уровнями рассчитывается по формуле:
где Средний абсолютный прирост исчисляется как среднее значение цепных абсолютных приростов
Среднее значение коэффициента роста
Средний темп роста
Средний темп прироста
Графический метод анализа временного ряда дает весьма приближенные результаты, поэтому необходимо использовать более строгие аналитические процедуры. Так, прежде чем перейти к выделению тренда, следует проверить гипотезу о том, существует ли он вообще. Решение данной задачи может быть основано на методе статистической проверки гипотез. Здесь используется проверка разности средних уровней. Для этого динамический ряд разбивается на две примерно равные по числу членов части. По каждой части находятся: Средние значения
Исправленные дисперсии
где
п – число членов динамического ряда; п1 – число членов первой части ряда; п2 – число членов второй части ряда (п = п1 + п2). Сначала проверяется гипотеза о равенстве дисперсий этих совокупностей на основе F – критерия Фишера – Спедекора. Для этого нужно определить расчетное значение этого критерия, сравнить его с табличным критическим при заданном уровне значимости
К1 = п1 – 1, К2 = п2 – 1. В данном случае п1 – число членов той части ряда, которому соответствует большая дисперсия ( Если Fрасч > Fкрит, то гипотеза о равенстве дисперсий отвергается и проверить гипотезу о наличии тренда в динамическом ряду методом сравнения средних уровней нельзя. Если Fрасч < Fкрит, расхождение между Находится расчетное значение t – критерия Стьюдента по формуле: t расч = ( Где
Расчетное значение t – критерия сравнивается с табличным критическим его значением при уровне значимости Например, табличные значения t – критерия следующие: t(0,1; 10) = 1,81; t(0,05; 10) = 2,23; t(0,01; 10) = 3,17. Если t расч < t крит, то делается вывод о том, что расхождение между Далее целесообразно выявить резкие отклонения от основного направления развития в тот или иной период и установить их истинную причину. В тех случаях, когда развитие явления носит скачкообразный характер и определить основную тенденцию этого процесса с помощью графика оказывается затруднительно, необходимо провести выравнивание ряда либо методом скользящего среднего, либо с помощью аналитического выравнивания. Итак, любому статистическому моделированию предшествует этап обработки эмпирических данных. Предварительная обработка исходного числового ряда направлена на решение следующих задач: снизить влияние случайной составляющей в исходном числовом ряду, т.е. приблизить его к тренду, представить информацию, содержащуюся в числовом ряду, в таком виде, чтобы существенно снизить трудность математического описания тренда. Основные инструменты для решения данных задач обозначены ранее. Процедура сглаживания направлена на минимизацию случайных отклонений точек ряда от некоторой гладкой кривой предполагаемого тренда процесса. Наиболее распространен способ осреднения уровня по некоторой совокупности окружающих точек, причем эта операция перемещается вдоль ряда точек, в связи с чем обычно называется скользящая средняя. В самом простом варианте сглаживающая функция линейна и сглаживающая группа состоит из предыдущей и последующей точек, в более сложных – функция нелинейна и использует группу произвольного числа точек. Сглаживание производится с помощью многочленов. Наилучшее сглаживание получается для средних точек группы, поэтому желательно выбирать нечетное количество точек в сглаживаемой группе. Сами группы точек берут по составу скользящими по всему ряду. Так, по первым точкам
где
Последние две формулы применяются обычно по краям интервала. Аналогичные формулы имеются для сглаживания рядов по пяти точкам:
Сглаживание даже в простом линейном варианте является во многих случаях весьма эффективным средством выявления тренда при наложении на эмпирический числовой ряд случайных помех и ошибок измерения. Для рядов со значительной амплитудой помехи имеется возможность проводить многократное сглаживание исходного числового ряда. Число последовательных циклов сглаживания должно выбираться в зависимости от вида исходного ряда, от степени предполагаемой его зашумленности помехой, от цели, которую преследует сглаживание. Надо иметь при этом в виду, что эффективность этой процедуры быстро уменьшается (в большинстве случаев), так что целесообразно повторять ее от одного до трех раз. Очень важным является вопрос о выборе периода скольжения средней. Если изучаемый ряд подвержен циклическим колебаниям, то период скольжения должен быть либо равным, либо кратным периоду колеблемости. Если подобные колебания отсутствуют, рекомендуется выполнить несколько вариантов выравнивания с разными периодами скольжения, пока основная тенденция не будет выявлена наиболее отчетливо. Когда выравнивается ряд небольшого числа уровней, то из-за «укорачивания» ряда выровненных значений использование многочисленных скользящих средних существенно ограничивается. Средние, рассчитанные по большому периоду скольжения, лучше выравнивают случайные колебания, но при этом ряд выровненных значений «укорачивается». Использование меньшего периода скольжения приводит к меньшему укорачиванию ряда, но в этом случае хуже гасится воздействие случайных факторов. Другим методом выравнивания динамического ряда является аналитическое выравнивание. При аналитическом выравнивании теоретические (расчетные) значения ряда определяют, исходя из предположения об их зависимости от времени
Задача заключается в выборе формы тренда, выражающей сущность изучаемого процесса, в расчете неизвестных параметров уравнения тренда ( Наиболее распространенными в экономике являются следующие регрессионные модели долговременных составляющих аналитической модели ряда динамики (функции тренда). 1. Линейная модель – полином первой степени 2. Степенная модель 3. Параболическая модель – полином второй степени 4. Показательная модель 5. Гиперболическая модель 6. Логарифмическая модель Выравнивание эмпирических данных по заданной функции начинается с определения ее параметров. Расчет параметров уравнения может быть произведен: - методом средних; - методом наименьших квадратов (МНК); - методом аппроксимации (метод последовательных приближений). Наиболее распространенным среди указанных методов является МНК. Аналитическое выравнивание эмпирических данных по МНК предполагает нахождение такого теоретического уровня, который удовлетворял бы следующим двум условиям: А) сумма линейных отклонений теоретических значений ряда
Б) сумма квадратов этих отклонений есть величина наименьшая:
Следует помнить, что МНК может использоваться для расчета параметров уравнения только в случае, когда, во-первых, выбранные уравнения линейны относительно своих параметров, а между учтенными и неучтенными факторами нет связи; и, во-вторых, отклонения эмпирических значений ряда от теоретического уровня подчиняются закону нормального распределения. Для вычисления параметров, которые не входят в уравнение линейно и когда никакими преобразованиями нельзя установить линейного соотношения между параметрами и уравнением, применяется метод последовательного приближения или метод аппроксимации. Согласно МНК, параметры уравнений искомой кривой показателя находятся из системы нормальных уравнений: Для линейной зависимости
При выборе зависимости может получиться так, что ряд динамики выравнивается несколькими видами зависимостей (наряду с линией может быть экспоненциальная зависимость). Задача исследователя состоит в выборе уравнения, которое в наибольшей степени соответствует характеру исследуемого процесса. Для этого используются статистические характеристики, в том числе, такие как сумма квадратов отклонений, корреляционное отношение (коэффициент парной корреляции), коэффициент детерминации. 1. Коэффициент корреляции находится по формуле: Ккор = Числитель в дроби – дисперсия, объясняемая регрессией. Знаменатель – общая дисперсия. 2. Коэффициент детерминации определяется как квадрат коэффициента корреляции. Самым простым способом определения сезонных составляющих является индекс сезонности:
где
Расчет индекса сезонности по одному году является ненадежным, так как в этом случае велика вероятность влияния случайных факторов. Поэтому на практике при расчете индекса сезонности пользуются месячными данными за К лет (в основном, не менее, чем за три года). В этом случае индекс сезонности равен:
где
Рекомендуемая литература: 13 (стр. 5 – 11; 24 – 28; 44 – 52; 80 – 224; 317 - 325), 14 (стр. 26 – 28; 35 – 44; 50 – 100), 15 (стр. 6 – 47; 52 – 64), 17 (стр. 42 – 92), 18 (стр. 9 – 64; 105 – 183), 19 (стр. 648 – 672), 20 (стр. 8 – 148; 175 – 216), 21 (стр. 7 – 21; 30 – 38; 41 – 124), 22 (стр. 36 – 141), 23 (стр. 124 – 147, 419 – 429), 25 (стр. 35 – 65), 26 (стр. 72 – 131; 180 - 277), 28 (глава «Системная концепция прогнозирования социально-экономических процессов», глава «Сценарный метод прогнозирования»)
Тема 4. Организация прогнозно-плановой работы на федеральном, региональном и корпоративном уровнях
Цель занятия: Формирование теоретических знаний и практических навыков в области организации прогнозно-плановой работы на федеральном, региональном и корпоративном уровнях.
Вопросы к практическому занятию: 1. Система органов планирования Российской Федерации.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 1260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.4 (0.013 с.) |

 сравнивают с предыдущим
сравнивают с предыдущим  . При базисном способе выбирают базисный уровень
. При базисном способе выбирают базисный уровень  и все остальные уровни сравнивают с ним. Для определения величины абсолютной скорости роста (снижения) значений уровней ряда динамики используют статистический показатель - абсолютный прирост ∆. Он показывает, на сколько единиц увеличилось значение уровня
и все остальные уровни сравнивают с ним. Для определения величины абсолютной скорости роста (снижения) значений уровней ряда динамики используют статистический показатель - абсолютный прирост ∆. Он показывает, на сколько единиц увеличилось значение уровня  =
=  =
=  =
=  ,
, 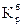 =
= 
 (3.1)
(3.1) ,
,  . (3.2)
. (3.2) цеп = цеп
цеп = цеп  ,
,  определяется как результат деления абсолютного прироста на соответствующий темп прироста:
определяется как результат деления абсолютного прироста на соответствующий темп прироста: (3.5)
(3.5) уровней ряда динамики зависит от его вида. Всего существует четыре вида средних.
уровней ряда динамики зависит от его вида. Всего существует четыре вида средних. (3.7)
(3.7) , (3.8)
, (3.8) - временная разность между данным
- временная разность между данным  . (3.9)
. (3.9) (3.10)
(3.10) -м и
-м и 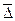 =
=  цеп или
цеп или 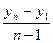 (3.11)
(3.11) равно среднему геометрическому цепных коэффициентов роста
равно среднему геометрическому цепных коэффициентов роста или
или  (3.12)
(3.12) есть средний коэффициент роста, выраженный в процентах:
есть средний коэффициент роста, выраженный в процентах: =
=  и
и  . (3.15)
. (3.15) и
и  . (3.16)
. (3.16) - уровень динамического ряда;
- уровень динамического ряда; - индекс уровня динамического ряда (
- индекс уровня динамического ряда ( и К1 и К2 степенями свободы – Fкр(
и К1 и К2 степенями свободы – Fкр( расч =
расч =  (3.18)
(3.18) max); п2 – число членов той части, которой соответствует меньшая дисперсия (
max); п2 – число членов той части, которой соответствует меньшая дисперсия ( и
и  несущественно (случайно). В этом случае проверяется основная гипотеза о равенстве двух частей динамического ряда на основе t – критерия Стьюдента.
несущественно (случайно). В этом случае проверяется основная гипотеза о равенстве двух частей динамического ряда на основе t – критерия Стьюдента.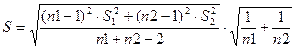 . (3.19)
. (3.19) и
и  незначимо (случайно), т.е. тенденция (тренд) отсутствует, если t расч > t крит, то расхождение между средними существенно, тенденция (тренд) существует.
незначимо (случайно), т.е. тенденция (тренд) отсутствует, если t расч > t крит, то расхождение между средними существенно, тенденция (тренд) существует.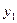 ,
,  ,
,  ,
,  ,
, 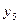 сглаживают среднюю
сглаживают среднюю  сглаживают
сглаживают 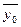 =
=  ; (3.20)
; (3.20) =
=  ); (3.21)
); (3.21)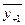 =
=  , (3.22)
, (3.22) ,
,  ,
,  (3.23)
(3.23)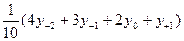 (3.24)
(3.24) (3.25)
(3.25) =
=  (3.26)
(3.26) =
=  . (3.27)
. (3.27) ^Y = f(t).
^Y = f(t). ) с помощью теории корреляции методом наименьших квадратов. Следовательно, для аналитического выравнивания могут использоваться разнообразные формы тренда.
) с помощью теории корреляции методом наименьших квадратов. Следовательно, для аналитического выравнивания могут использоваться разнообразные формы тренда. (Полином – многочлен)
(Полином – многочлен)




 от эмпирических равна нулю:
от эмпирических равна нулю: (3.28)
(3.28)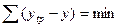 (3.29)
(3.29) (3.30)
(3.30)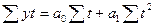
 (3.31)
(3.31) , (3.32)
, (3.32)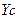 - значение уровня ряда динамики, соответствующее интересующему нас интервалу времени (сезону);
- значение уровня ряда динамики, соответствующее интересующему нас интервалу времени (сезону); - среднее значение уровней ряда динамики.
- среднее значение уровней ряда динамики. , (3.33)
, (3.33) - среднее значение уровня за К лет.
- среднее значение уровня за К лет. ,
,  =
=  (3.34)
(3.34)


