
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фиктивные переменные в регрессионных моделяхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ГЛАВА 4. НЕКОТОРЫЕ ВОПРОСЫ СПЕЦИФИКАЦИИ РЕГРЕССИОННЫХ МОДЕЛЕЙ
К основным вопросам спецификации модели традиционно относят два типа задач. Первый – это выбор структуры уравнения регрессии, т. е. математической формы модели. Второй – это определение качественного и количественного состава объясняющих переменных (факторов-аргументов). Неправильные постановка и решение этих задач приводят к появлению в создаваемых моделях ошибок спецификации. Можно заметить, что при проведении эконометрического анализа приходится постоянно сталкиваться с вопросами спецификации модели, например, при определении значимости регрессоров, при рассмотрении мультиколлинеарности и т. д. В целом работоспособной является модель с правильной спецификацией. Это означает, что уравнение регрессии достаточно надежно определяет соотношение между исследуемыми экономическими показателями. В данной главе рассмотрены наиболее общие вопросы спецификации, позволяющие учитывать реальные ситуации, возникающие при эконометрическом моделировании.
Нелинейная регрессия
В силу многообразия и сложности экономических процессов невозможно ограничиться рассмотрением лишь линейных регрессионных моделей, т. к. многие экономические зависимости являются нелинейными по своей сути. Например, при анализе зависимости общих издержек от объема выпуска наиболее обоснованной является полиномиальная модель. При рассмотрении производственных функций обычно используются модели, содержащие показательные функции (например, широко известная в экономике функция Кобба-Дугласа). Мы ограничимся рассмотрением нелинейных моделей, допускающих их сведение к линейным путем преобразования переменных. В рамках этого подхода для линеаризации могут быть использованы модели как нелинейные по переменным, так и нелинейные по параметрам. Наиболее просто осуществляется линеаризация, если модель нелинейна по переменным. В этом случае введением новых переменных модель можно свести к линейной, для оценки параметров которой используется обычный метод наименьших квадратов. Рассмотрим некоторые примеры моделей, линейных по параметрам [11]. Кубическая функция вида
в микроэкономике моделирует зависимость общих издержек (U) от объема выпуска (Q) (рис. 4.1а).
Аналогично квадратичная функция
может отражать зависимость между объемом выпуска (Q) и средними (
а б в Рис. 4.1.
Заменяя Х на Х 1, Х 2 на Х 2, Х 3 на Х 3, получаем вместо (4.1) и (4.2) модели множественной линейной регрессии, где исходные факторные данные необходимо представлять в соответствующих степенях. Модель вида
называется обратной моделью. Эта модель сводится к линейной парной регрессии заменой
Рис. 4.2.
Более сложной проблемой является нелинейность модели по параметрам, т. к. в данном случае при применении МНК к линеаризованным моделям необходимо учитывать результаты преобразования случайного отклонения e. К числу таких моделей можно отнести, например, мультипликативную (степенную) модель
и экспоненциальную модель
Подобные модели могут быть сведены к линейным логарифмированием обеих частей уравнений. Тогда, например, модель (4.4) примет вид lnY = lnb 0 + b 1 lnX + ln e. (4.6) Полученное уравнение является линейным относительно логарифмов переменных, т. е. модель может быть оценена и проанализирована обычными методами линейного регрессионного анализа. Однако следует заметить, что для эффективного применения МНК в данной модели случайное отклонение e должно иметь логарифмически нормальное распределение. Приведенная модель (4.6) называется логарифмической и легко обобщается на большее число переменных. В качестве примера использования линеаризирующего преобразования рассмотрим регрессионную модель на основе производственной функции Кобба-Дугласа Y = AK a L β, (4.7) где Y – объем производства; K – затраты капитала; L – затраты труда; A, a и β – параметры модели. Показатели a и β являются коэффициентами частной эластичности объема производства по затратам капитала и труда соответственно. Это означает, что при увеличении одних только затрат капитала (труда) на 1 % объем производства увеличивается на a %(β %). Сумма этих коэффициентов является таким важным экономическим показателем, как отдача от масштаба производства. При a + β = 1 говорят о постоянной отдаче от масштаба (во сколько раз увеличиваются затраты ресурсов, во столько же раз увеличивается объем производства). При a + β < 1 имеет место убывающая отдача от масштаба (увеличение объема производства меньше увеличения затрат). В случае a + β > 1 наблюдается возрастающая отдача от масштаба (увеличение объема производства больше увеличения затрат ресурсов).
Учитывая возможное влияние неучтенных и случайных факторов, добавим в модель (4.7) случайное отклонение: Y = AK a L βe. (4.8) Полученную мультипликативную модель легко свести к линейной путем логарифмирования. Тогда, прологарифмировав (4.8), для конкретного i -го наблюдения имеем: lnyi = lnA + a lnKi + β lnLi + ln e i, i = 1, …, n. (4.9) Если производственная ситуация соответствует постоянной отдаче от масштаба (a + β = 1), то модель на основе функции Кобба-Дугласа представляется в виде: Y = AK a L 1 - ae, или (4.10)
Таким образом, получаем зависимость производительности труда (Y / L) от его капиталовооруженности (K / L). Для оценки параметров модели (4.10) приводим ее к линейной парной регрессии ln(Y/L)i = lnA + a ln(K/L)i + ln e, i = 1, …, n. (4.11) В эконометрическом анализе используется также производственная функция Кобба-Дугласа с учетом научно-технического прогресса: Y = AK a L βеq t e, (4.12) где t – время; q – параметр, характеризующий темп прироста объема производства благодаря техническому прогрессу. Модель (4.12) сводится к линейной регрессии аналогично модели (4.8). Следует заметить, что модель вида
отличается от (4.4) тем, что случайное отклонение здесь входит аддитивно, нельзя привести логарифмированием к линейному уравнению. В этом случае используются специальные итерационные процедуры оценивания параметров. Пример 4.1. По данным, собранным по 20 предприятиям (n = 20), оценить производственную функцию Кобба-Дугласа при постоянной отдаче от масштаба. Рассмотрим функцию Кобба-Дугласа в виде (4.10). Исходные переменные модели K / L и Y / L. Логарифмируя и применяя к преобразованным данным МНК, получим*
стандартные ошибки (0,15) (0,04) или в виде Коэффициент регрессии, равный 0,25, является также коэффициентом эластичности в рамках данной модели. Он показывает, что при увеличении капиталовооруженности труда на 1 % производительность труда на предприятиях отрасли увеличивается в среднем на 0,25 %. Сравнивая наблюдаемое (расчетное) и табличное (критическое) значения t-статистики на уровне значимости a = 0,05, делаем вывод о том, что коэффициент регрессии, а значит и уравнение парной регрессионной модели, значимы.
Тест Грегори Чоу
В том случае, когда фиктивная переменная действует на коэффициент при объясняющей переменной, линия модели отличается от той, которая была до уровня х 0 (рис. 4.3б), что соответствует разбиению выборочных данных на две части (группы) и рассмотрению отдельных уравнений регрессии по каждой выборке (подвыборке). В практических исследованиях достаточно часто возникает вопрос, имеет ли смысл разбивать выборку на части и строить так называемою кусочно-линейную модель с фиктивными переменными (рис. 4.3б) или ограничиться «обыкновенной» общей регрессией для всего диапазона точек наблюдений?
Для ответа на этот вопрос обычно используется тест (критерий) Грегори Чоу [1,28], суть которого заключается в следующем. Пусть общая выборка имеет объем n Через S 0 обозначим сумму квадратов отклонений Очевидно, что равенство S 0 = S 1 + S 2 выполняется лишь при совпадении коэффициентов регрессии для всех трех уравнений. Тогда отклонение S 0 - (S 1 + S 2) может быть использовано как показатель улучшения качества модели при разбиении интервала наблюдений на две подвыброки, так как чем сильнее различие в поведении Y для каждой из подвыборок, тем больше значение S 0 будет превосходить сумму S 1 + S 2. Следовательно, отношение [ S 0 - (S 1 + S 2)]/(m + 1) будет определять оценку уменьшения дисперсии регрессии за счет построения двух уравнений вместо одного. При разбиении общей выборки число степеней свободы сократится на (m + 1), т. к. теперь вместо (m + 1) параметра объединенной регрессионной модели необходимо оценивать (2 m + 2) коэффициента двух регрессий. В данном случае соотношение (S 1 + S 2)/(n - 2 m - 2) выражает необъясненную дисперсию зависимой переменной при рассмотрении двух регрессий. Приведенные выше рассуждения позволяют сделать вывод о том, что общую выборку целесообразно разбивать на два интервала только в том случае, если соответствующее уменьшение дисперсии будет значимо больше оставшейся необъясненной дисперсии. Этот вывод может быть основан на стандартной процедуре сравнения дисперсий на основе F -статистики, наблюдаемое значение которой для данного анализа имеет вид:
где m - число количественных объясняющих переменных в уравнениях регрессии (m - одинаково для всех трех уравнений модели). Если Fнабл < Fкр при заданном уровне значимости a и соответствующих числах степеней свободы v 1 = m + 1 и v 2 = n - 2 m - 2, то можно считать, что различие между S 0 и S 1 + S 2 статистически незначимо и нет смысла разбивать уравнение модели на части путем введения фиктивных переменных. Следует заметить, что фактически мы тестируем гипотезу Н 0 о равенстве коэффициентов b уравнений регрессии, построенных по каждой подвыборке. Если нулевая гипотеза Н 0 верна, то две регрессионные модели можно объединить в одну, построенную по выборке объема n = n 1 + n 2.
Ошибки спецификации
Построение работоспособной эконометрической модели возможно при условии достаточно хорошей (правильной) спецификации уравнения регрессии. Выполнение условия правильной спецификации модели базируется на надежности выводов предмодельного качественного анализа исследуемого объекта, а также на результатах методик, направленных на устранение или корректировку ошибок спецификации, которые весьма нередки, особенно на начальном этапе эконометрического анализа. К основным ошибкам спецификации следует отнести выбор неправильной функциональной формы модели, отбрасывание (невключение) значимой переменной, добавление (включение) незначимой переменной. Выбор неправильной функциональной формы модели, например, использование вместо правильной линейной модели полиномиального уравнения с теми же переменными, приводит к серьезным отрицательным последствиям. Обычно такая ошибка вызывает ухудшение статистических свойств оценок коэффициентов регрессии и прогнозных качеств модели. С точки зрения регрессионного анализа в данном случае наблюдается нарушение условий Гаусса-Маркова для случайных отклонений. Критерием прогнозных качеств оцененной регрессионной модели может служить следующее соотношение:
где Если возможно провести сравнение моделей различной функциональной формы, но содержащих одинаковый набор переменных, то выбирается модель с наибольшим скорректированным коэффициентом детерминации Для случая парной (однофакторной) регрессионной модели подбор функциональной формы обычно осуществляется по виду расположения точек наблюдений на корреляционном поле. Для оцененной парной регрессии о правильности выбора функциональной формы можно судить по значениям коэффициента детерминации и средней ошибки аппроксимации. Для множественной регрессии ситуация более неоднозначна, так как графическое представление статистических данных в этом случае невозможно. Здесь детальный анализ адекватности функциональной формы модели и ошибок спецификации в целом может быть проведен на основе специальных тестов, подробное описание которых выходит за рамки данной книги. Суть тестов по обнаружению неправильной спецификации модели основана на исследовании поведения случайных отклонений еi [11,28]. В целом следует заметить, что даже правильно специфицированная на данном этапе эконометрическая модель должна постоянно совершенствоваться, исходя из меняющихся условий функционирования экономических систем. Совершенствование модели с целью лучшего соответствия экспериментальным данным может приводить к изменению вида функциональных связей между переменными и набора факторов-аргументов.
Рассмотрим следующую, достаточно распространенную ошибку спецификации, которая характеризуется как невключение значимой переменной в уравнение регрессии. Пусть, например, объясняемая переменная Y линейно зависит от двух факторов-аргументов Х 1 и Х 2, и истинная модель имеет вид: Y = b 0 + b 1 Х 1 + b 2 Х 2 + e. (4.25) Однако исследователь, в силу недостатка информации об экономическом объекте или неправильной ее обработки, ошибочно считает, что на переменную Y реально воздействует лишь переменная Х 1 и оценивает регрессию
для которой Последствия допущенной ошибки выражаются в том, что оценки параметров, полученные с помощью МНК по уравнению (4.26), являются смещенными ( С учетом выполнения (4.25) коэффициент
По условию классической регрессионной модели переменные Х 1 и Х 2 являются детерминированными (нестохастическими). Тогда Cov (Х 1, e) = 0 и для математического ожидания оценки параметра
Таким образом, в соответствии с (4.28) оценка Отметим, что невключение переменной существенно отражается на коэффициенте детерминации R 2, завышая влияние фактора-аргумента Х 1 на объясняемую дисперсию результирующей переменной Y. Смещенные оценки параметров модели могут приводить к ложным выводам соответствующих статистических тестов (статистических поверок гипотез). Рассмотрим следующую ситуацию. Пусть уравнение Y = b 0 + b 1 Х 1 + e (4.29) представляет истинную модель, а мы заменяем ее более сложной моделью (4.25), совершая при этом ошибку добавления (включения) незначимой переменной. Последствия данной ошибки не являются столь серьезными, как в предыдущем случае. Оценки параметров Вывод об увеличении стандартных ошибок и неэффективности оценок можно проиллюстрировать формулами (2.22) и (3.26) расчета дисперсий оценок коэффициентов для уравнений (4.29) и (4.25) соответственно:
Здесь S 2 - дисперсия случайных отклонений; r 12 – коэффициент корреляции между объясняющими переменными Х 1 и Х 2. Таким образом, дисперсия для парной регрессии
Вопросы и упражнения для самопроверки
1. Что понимается под спецификацией модели? 2. Каковы признаки качественной регрессионной модели? 3. Приведите примеры нелинейных моделей в экономике. 4. Опишите методы линеаризации моделей. 5. Какие требования предъявляются к свойствам случайных отклонений при линеаризации? 6. Что отражает производственная функция Кобба-Дугласа; как можно построить и оценить модели на ее основе? 7. По имеющимся статистическим данным оцените параметры b 0 и b 1 следующей экспоненциальной модели:
8. Как формализованно можно представить качественные факторы в регрессионной модели? 9. Что описывают и как выражаются фиктивные переменные? 10. Сформулируйте правило использования фиктивных переменных в случае нескольких (k) градаций качественного признака. 11. Опишите, как можно использовать фиктивные переменные в сезонном анализе. 12. С помощью фиктивной переменной напишите уравнение парной регрессии, соответствующее структурному изменению, произошедшему в момент времени 13. Напишите уравнение множественной регрессионной модели, отражающей зависимость средней цены на двухкомнатную квартиру (Y) от следующих факторов: жилая площадь; площадь нежилых помещений, включая кухню; расстояние от центра города; расположение квартиры (первый или последний этаж); строительный материал (дом кирпичный или панельный); наличие или отсутствие лифта. 14. Сформулируйте цель и последовательность проведения теста Г. Чоу. 15. Как можно проверить гипотезу о том, что величина дохода влияет на «склонность к потреблению»? 16. Перечислите основные виды ошибок спецификации. 17. Охарактеризуйте основные виды ошибок спецификации и их последствия. 18. Как можно обнаружить ошибки спецификации?
ОСТАТКАМИ
Гетероскедастичность
Обобщенные линейные регрессионные модели, в которых дисперсии остатков не сохраняют постоянного уровня при переходе от одного наблюдения к другому (т. е. от одного значения объясняющей переменной к другому), называются моделями с гетероскедастичными остатками. В этом случае D (e i) ¹ D (e j), где D (e) – дисперсия остатков. Гетероскедастичность случайных отклонений – вполне естественная ситуация при анализе пространственных выборочных данных. Кроме того, в выборке могут присутствовать так называемые «выбросы» (аномальные наблюдения), обработка которых представляет собой отдельную статистическую задачу [33]. Применение обычного МНК для оценки регрессионной модели с гетероскедастичностью приводит к тому, что оценка вектора параметров B, оставаясь несмещенной и состоятельной, не будет оптимальной в смысле теоремы Гаусса-Маркова, т. е. наиболее эффективной. Стандартные ошибки оценок будут рассчитаны со смещением и, вследствие этого, результаты по анализу точности и значимости построенной модели оказываются непригодными. Поэтому модели с гетероскедастичностью следует рассматривать в рамках ОМНК. В целом, прежде чем сделать вывод о возможности практического использования построенной регрессионной модели, необходимо установить наличие или отсутствие гетероскедастичности в каждом конкретном случае. При обнаружении гетероскедастичности далее решается задача по устранению или уменьшению влияния этого нежелательного эффекта.
Автокорреляция
При анализе временных рядов часто приходится учитывать статистическую зависимость (коррелированность) наблюдений в разные моменты времени. Следовательно, в данном случае для регрессионных моделей Cov (e i, e j) ¹ 0, i ¹ j, т. е. третья предпосылка Гаусса-Маркова о некоррелированности остатков не выполняется. Такие регрессионные зависимости называются моделями с автокорреляцией (сериальной корреляцией) остатков [1,28]. Для обобщенной линейной регрессионной модели с автокорреляцией ковариационная матрица случайных отклонений W не может быть диагональной. Последствия автокорреляции остатков во многом сходны с последствиями гетероскедастичности (см. раздел 5.2). Среди них особенно следует выделить ухудшение прогнозных качеств моделей временных рядов. Поскольку автокорреляция рассматривается в регрессионном анализе при использовании данных временных рядов, в дальнейших выкладках вместо символа i порядкового номера наблюдения будем использовать символ t отражающий момент наблюдения во времени (t = 1, 2, …, n). В экономических задачах более часто встречается так называемая положительная автокорреляция (Cov (e t - 1, e t) > 0 для соседних отклонений), нежели отрицательная автокорреляция (Cov (e t - 1, e t) < 0). В большинстве случаев причиной положительной автокорреляции является направленное постоянное воздействие на исследуемый показатель некоторых неучтенных в модели факторов, что отражается на поведении случайного отклонения e t. Пусть, например, исследуется спрос Y (yt) на прохладительные напитки в зависимости от дохода потребителей X по ежемесячным данным. Трендовая зависимость (основная тенденция), отражающая увеличение спроса с ростом дохода, может быть представлена линейной моделью
Рис. 5.2.
Если рассматривать в качестве примера временной ряд yt значений курса некоторой ценной бумаги, наблюдаемых в последовательные моменты времени, то естественно предположить, что результаты предыдущих торгов оказывают влияние на результаты последующих: завышенный (заниженный) в какой то момент времени курс скорее всего окажется завышенным (заниженным) по сравнению с реальным и на следующих торгах, т. е. здесь также может иметь место положительная автокорреляция. Графически положительная автокорреляция выражается в чередовании зон, где наблюдаемые значения оказываются выше модельных (предсказанных), и зон, где наблюдаемые значения ниже (рис. 5.2). Отрицательная автокорреляция характеризуется тем, что за положительным отклонением следует отрицательное и наоборот (принцип «маятника»). Примерная схема рассеивания точек относительно линии модели в случае отрицательной автокорреляции представлена на рис. 5.3.
Рис. 5.3.
Следует заметить, что автокорреляция чаще всего может быть вызвана неправильной спецификацией модели. Поэтому для ее возможного устранения следует скорректировать саму модель: включить в уравнение регрессии дополнительный фактор-аргумент или изменить формулу зависимости. Однако это далеко не всегда приводит к положительным результатам, что вызвано сложностью экономических процессов, влияющих на поведение случайных отклонений e t. Если возможные процедуры изменения спецификации модели оказываются неэффективными, то необходимо воспользоваться так называемыми авторегрессионными преобразованиями над случайными отклонениями, среди которых наиболее простым и результативным является авторегрессионный процесс (авторегрессия) первого порядка. Авторегрессия первого порядка состоит в достаточно реалистичном предположении, что корреляция во времени наиболее сильно проявляется между двумя соседними отклонениями. В целом для построения качественных моделей (особенно моделей временных рядов), наряду с проверкой общего качества уравнений регрессии, необходимо проводить их проверку на наличие автокорреляции остатков, и, в случае обнаружения, применять специальные методы по ее устранению.
Обнаружение автокорреляции
Большинство тестов на наличие автокорреляции основаны на достаточно простой идее: если корреляция во времени присутствует между случайными отклонениями e t, то она должна проявляться и в их оценках et, получаемых при использовании обычного МНК. Наиболее распространенным примером реализации данного подхода является тест (критерий) Дарбина-Уотсона, который определяет наличие автокорреляции между соседними отклонениями [1,22,28]. Этот критерий основан на применении статистики Дарбина-Уотсона (DW), определяемой соотношением:
Покажем, что статистика Дарбина-Уотсона связана с выборочным коэффициентом корреляции между соседними отклонениями r следующим образом: DW» 2(1 - r). (5.11) Преобразуем соотношение (5.10)
При достаточно больших выборках сумма
Учитывая, что математическое ожидание M (et) = 0, запишем формулу для вычисления выборочного коэффициента корреляции:
При большом числе наблюдений n суммы
Из сравнения выражений (5.13) и (5.14) следует приближенное равенство (5.11). Согласно формуле (5.11) значения статистики Дарбина-Уотсона могут находиться в пределах 0 £ DW £ 4 и указывают на наличие либо отсутствие автокорреляции. Действительно, если автокорреляция отсутствует, то выборочный коэффициент корреляции между соседними отклонениями r» 0 и значение статистики DW будет близко к двум, что соответствует независимости случайных отклонений. Близость наблюдаемого значения статистики к нулю указывает на наличие положительной автокорреляции, к четырем – отрицательной автокорреляции. Следует заметить, что непосредственное использование статистики DW в схеме проверки статистических гипотез (H 0: r = 0, H 1: r > 0, r < 0) не представляется возможным. Проблема состоит в том, что распределение статистики DW зависит не только от числа наблюдений n и количества регрессоров m, но и от значений объясняющих переменных. В этом случае пороговые (критические) значения статистики указать невозможно. Однако Дарбин и Уотсон доказали, что для статистики существуют две границы (du - верхняя, dl - нижняя), которые зависят только от n, m и выбираемого уровня значимости a. Значения этих границ статистики DW затабулированы (см. Приложение 6) и могут быть использованы для проверки нулевой гипотезы H 0 об отсутствии автокорреляции. Приведем общую схему применения теста (критерия) Дарбина-Уотсона [11,28,29]. 1. По построенному с помощью МНК эмпирическому уравнению регрессии:
определяются значения отклонений (остатков) 2. По формуле (5.10) на основе полученных данных рассчитывается наблюдаемое значение статистики DW. 3. По таблице критических значений статистики DW определяются два числа dl и du и делаются выводы о наличии автокорреляции по правилу, отраженному следующей таблицей.
Таблица 5.1
Статистика Дарбина-Уотсона приводится во всех компьютерных эконометрических пакетах как важная характеристика качества регрессионной модели. Несмотря на то, что тест Дарбина-Уотсона наиболее распространен в регрессионном анализе, он обладает рядом ограничений и недостатков. Его основными недостатками являются наличие зоны неопределенности для значений статистики, когда нет оснований ни принимать, ни отвергать гипотезу H 0 об отсутствии автокорреляции, а также неприменимость для так называемых авторегрессионных моделей*, содержащих в составе объясняющих переменных зависимую переменную с временным лагом в один период.
ГЛАВА 4. НЕКОТОРЫЕ ВОПРОСЫ СПЕЦИФИКАЦИИ РЕГРЕССИОННЫХ МОДЕЛЕЙ
К основным вопросам спецификации модели традиционно относят два типа задач. Первый – это выбор структуры уравнения регрессии, т. е. математической формы модели. Второй – это определение качественного и количественного состава объясняющих переменных (факторов-аргументов). Неправильные постановка и решение этих задач приводят к появлению в создаваемых моделях ошибок спецификации. Можно заметить, что при проведении эконометрического анализа приходится постоянно сталкиваться с вопросами спецификации модели, например, при определении значимости регрессоров, при рассмотрении мультиколлинеарности и т. д. В целом работоспособной является модель с правильной спецификацией. Это означает, что уравнение регрессии достаточно надежно определяет соотношение между исследуемыми экономическими показателями. В данной главе рассмотрены наиболее общие вопросы спецификации, позволяющие учитывать реальные ситуации, возникающие при эконометрическом моделировании.
Нелинейная регрессия
В силу многообразия и сложности экономических процессов невозможно ограничиться рассмотрением лишь линейных регрессионных моделей, т. к. многие экономические зависимости являются нелинейными по своей сути. Например, при анализе зависимости общих издержек от объема выпуска наиболее обоснованной является полиномиальная модель. При рассмотрении производственных функций обычно используются модели, содержащие показательные функции (например, широко известная в экономике функция Кобба-Дугласа). Мы ограничимся рассмотрением нелинейных моделей, допускающих их сведение к линейным путем преобразования переменных. В рамках этого подхода для линеаризации могут быть использованы модели как нелинейные по переменным, так и нелинейные по параметрам. Наиболее просто осуществляется линеаризация, если модель нелинейна по переменным. В этом случае введением новых переменных модель можно свести к линейной, для оценки параметров которой используется обычный метод наименьших квадратов. Рассмотрим некоторые примеры моделей, линейных по параметрам [11]. Кубическая функция вида
в
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.74 (0.015 с.) |

 (4.1)
(4.1) (4.2)
(4.2) ) издержками (рис. 4.1б); или расходами на рекламу (С) и прибылью (П) (рис. 4.1в).
) издержками (рис. 4.1б); или расходами на рекламу (С) и прибылью (П) (рис. 4.1в).



 (4.3)
(4.3)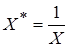 . Подобные модели обычно применяются в тех случаях, когда неограниченное увеличение объясняющей (факторной) переменной Х асимптотически приближает зависимую переменную Y к некоторому пределу (в данном случае к b 0). Например, данная модель может отражать зависимость между доходом Х и спросом на определенные товары Y (рис. 4.2).
. Подобные модели обычно применяются в тех случаях, когда неограниченное увеличение объясняющей (факторной) переменной Х асимптотически приближает зависимую переменную Y к некоторому пределу (в данном случае к b 0). Например, данная модель может отражать зависимость между доходом Х и спросом на определенные товары Y (рис. 4.2).
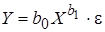 (4.4)
(4.4) . (4.5)
. (4.5)
 (4.13)
(4.13)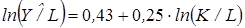 ,
, .
. выборочных данных от их модельных оценок, полученных по общему уравнению регрессии. Разобьем выборку на две подвыборки объемами n 1 и n 2 соответственно (n 1 + n 2 = n). Будем считать, что для каждой подвыборки можно построить уравнения регрессии одного вида, но с разными коэффициентами b. Через
выборочных данных от их модельных оценок, полученных по общему уравнению регрессии. Разобьем выборку на две подвыборки объемами n 1 и n 2 соответственно (n 1 + n 2 = n). Будем считать, что для каждой подвыборки можно построить уравнения регрессии одного вида, но с разными коэффициентами b. Через  и
и  обозначим соответствующие суммы квадратов отклонений. Далее рассмотрим некоторые соотношения.
обозначим соответствующие суммы квадратов отклонений. Далее рассмотрим некоторые соотношения. (4.23)
(4.23) , (4.24)
, (4.24)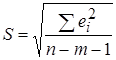 – стандартная ошибка регрессии,
– стандартная ошибка регрессии,  - среднее значение зависимой переменой уравнения регрессии. Величина d определяет относительную ошибку прогноза.
- среднее значение зависимой переменой уравнения регрессии. Величина d определяет относительную ошибку прогноза.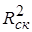 и наименьшей величиной d.
и наименьшей величиной d. (4.26)
(4.26)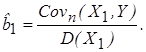
 ) и несостоятельными даже при неограниченно большом числе наблюдений. Покажем это для оценки
) и несостоятельными даже при неограниченно большом числе наблюдений. Покажем это для оценки  .
.


 (4.27)
(4.27) получим следующее выражение:
получим следующее выражение: (4.28)
(4.28) Знак (направление) смещения зависит от знаков величин
Знак (направление) смещения зависит от знаков величин  и Cov (Х 1, Х 2). Например, при положительном параметре
и Cov (Х 1, Х 2). Например, при положительном параметре  и
и 
 .
.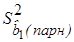 оказывается меньше дисперсии для множественной регрессии
оказывается меньше дисперсии для множественной регрессии  , которая неограниченно возрастает при стремлении r 12 к 1.
, которая неограниченно возрастает при стремлении r 12 к 1. .
.
 (рис. 5.2). Однако фактические точки наблюдений вследствие влияния фактора сезонности будут превышать трендовую линию в летние периоды и находиться ниже ее в зимние.
(рис. 5.2). Однако фактические точки наблюдений вследствие влияния фактора сезонности будут превышать трендовую линию в летние периоды и находиться ниже ее в зимние.
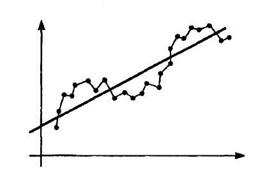


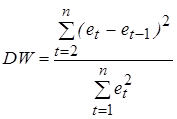 . (5.10)
. (5.10)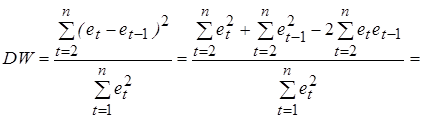
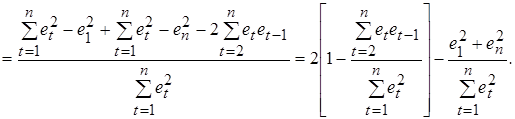 (5.12)
(5.12)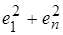 значительно меньше
значительно меньше 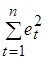 , поэтому последним членом в формуле (5.12) можно пренебречь. Тогда получим:
, поэтому последним членом в формуле (5.12) можно пренебречь. Тогда получим: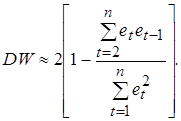 (5.13)
(5.13)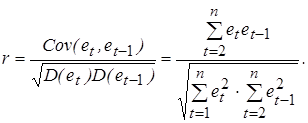
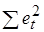 и
и 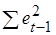 будут практически одинаковы. Поэтому выборочный коэффициент корреляции r можно приближенно представить в виде:
будут практически одинаковы. Поэтому выборочный коэффициент корреляции r можно приближенно представить в виде: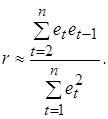 (5.14)
(5.14)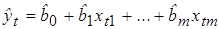
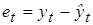 для каждого конкретного наблюдения t, t = 1, 2, …, n.
для каждого конкретного наблюдения t, t = 1, 2, …, n.


