
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценивание моделей с автокоррелируемыми остаткамиСодержание книги
Поиск на нашем сайте
Рассмотрение процедур оценивания моделей с автокорреляцией остатков будем проводить в рамках упрощающих предположений о том, что согласно имеющимся выборочным данным xt, yt задана модель парной линейной регрессии Y = b 0 + b 1 + e, (5.15) случайные отклонения которой подвержены воздействию авторегрессии первого порядка e t = re t - 1 + ut, (5.16) где ut (t = 2, 3, …, n) - случайные отклонения, удовлетворяющие предпосылкам МНК, а коэффициент авторегрессии r известен. Тогда наблюдениям t и t - 1 будут соответствовать уравнения: yt = b 0 + b 1 xt + e t (5.17) yt - 1 = b 0 + b 1 xt - 1 + e t - 1. (5.18) Вычтем из (5.17) уравнение (5.18), умноженное на r: yt - r yt - 1 = b 0(1 - r) + b 1(xt - r xt - 1) + (e t - re t - 1). (5.19) Далее введем обозначения
Полученная модель (5.20) является классической, так как новые случайные отклонения ut являются независимыми и имеют постоянную дисперсию, и может быть оценена по МНК. Следует заметить, что в результате проведенных преобразований мы теряем первое наблюдение, так как соотношение (5.19) имеет смысл только при t ³ 2. Число степеней свободы уменьшится на единицу, что может привести к определенной потере эффективности для моделей, базирующихся на выборках небольшого объема. Исходную информацию можно сохранить, если воспользоваться преобразованием, которое носит название поправки Прайса-Уинстона для первого наблюдения. Указанное преобразование заключается в том, что при t = 1 обе части уравнения (5.17) умножаются на
(5.21)
При достаточно большом числе наблюдений (n ³ 15) поправка Прайса-Уинстона практически не влияет на результаты анализа, поэтому ее можно не учитывать, оставляя значения первого наблюдения неопределенными. Отметим, что авторегрессионное преобразование может быть обобщено на произвольное число объясняющих переменных, т. е. использовано для модели множественной линейной регрессии. Для получения наиболее эффективных оценок вектора параметров В в такой модели применим обобщенный метод наименьших квадратов (ОМНК) при известном значении коэффициента r. Можно показать, что если последовательность остатков {e t } образует стационарный случайный процесс, когда дисперсии и ковариации не зависят от момента времени t (D (e t) = D (e t - 1) = σ2), то коэффициент авторегрессии первого порядка в точности равен коэффициенту корреляции между двумя соседними отклонениями. В общем случае, для различных наблюдений
Пользуясь (5.22), а также учитывая, что для случая авторегрессионного преобразования первого порядка выполнятся равенство
Обычно на практике значение коэффициента r априорно неизвестно, поэтому его необходимо оценивать. Наиболее простой способ оценки r заключается в применении обычного метода наименьших квадратов к регрессионному уравнению (5.16). Если оценка Существуют методы оценивания, основанные на применении статистики Дарбина-Уотсона. Напомним, что статистика DW выражается через выборочный коэффициент корреляции между соседними отклонениями согласно соотношению (5.11): DW» 2(1 - r). Тогда в качестве оценки коэффициента r может быть взят коэффициент r, который определяется из приближенного равенства (5.11):
Для данного метода оценка r коэффициента r будет достаточно точной при большом числе наблюдений. Наиболее точными методами оценивания параметра r являются итеративные процедуры, которые реализованы в большинстве компьютерных эконометрических пакетов. Эти процедуры основаны на предположении, что автокорреляция остатков описывается авторегрессионной схемой первого порядка (5.16). Рассмотрим один из наиболее распространенных итерационных процессов, называемый методом Кохрейна-Оркатта [11,28]. Опишем указанный метод на примере парной регрессии (5.17): yt = b 0 + b 1 xt + e t, где для случайных отклонений справедливо авторегрессионное преобразование первого порядка (5.16) e t = re t - 1 + ut. Метод Кохрейна-Оркатта включает в себя следующие этапы: 1. На основе имеющихся выборочных данных оценивается по МНК уравнение регрессии (5.17) и для него определяются оценки 2. Оценивается регрессия (5.16), в результате чего получается оценка 3. На основе найденной оценки
Оценивая регрессию (5.24) по МНК, получаем пересмотренные оценки 4. Значения Чередование этапов осуществляется до тех пор, пока очередное приближение r будет мало отличаться от предыдущего, т. е. пока оценки на двух последних шагах не совпадут с требуемой точностью.
Вопросы и упражнения для самопроверки
1. Какие предпосылки МНК могут не выполняться при рассмотрении реальных экономических ситуаций? 2. Что выключают в себя понятия классической и обобщенной модели; в чем суть обобщенного метода наименьших квадратов (ОМНК)? 3. Что такое гетероскедастичность случайных отклонений и каковы ее последствия при оценивании моделей? 4. Перечислите основные методы обнаружения гетероскедастичности. 5. Опишите схему теста ранговой корреляции Спирмена. 6. Опишите схему теста Голдфелда-Квандта. 7. Какие статистики используются в тестах проверки на присутствие гетероскедастичности. 8. Сформулируйте, в чем заключается сущность взвешенного метода наименьших квадратов (ВМНК)? Поясните, почему в случае наличия гетероскедастичности ВМНК позволяет получить более эффективные оценки, чем обычный МНК. 9. В результате рассмотрения регрессионной модели 10. Что такое автокорреляция? 11. Назовите причины и признаки положительной и отрицательной автокорреляции. 12. Опишите схему применения статистики Дарбина-Уотсона. 13. Поясните смысл авторегрессионного преобразования первого порядка. 14. Опишите способы оценки коэффициента корреляции между случайными отклонениями (остатками). 15. По таблице критических точек Дарбина-Уотсона при a = 0,05 определите значения статистики DW, дающие основание отклонить гипотезу Н 1 о наличии автокорреляции остатков для моделей, построенных по выборке объема n и содержащих число объясняющих переменных m: а) n = 20, m = 1; б) n = 25, m = 2; в) n = 50, m = 4. Сравните полученные результаты, сделайте выводы. 16. По статистическим данным за 10 лет построена регрессионная модель, отражающая зависимость между ценой определенного товара (блага) и объемом его продаж, для которой DW = 0,71. а) Будет ли в данном случае иметь место автокорреляция остатков? Если да, то она положительная или отрицательная? б) Что может служить причиной автокорреляции? в) Какими могут быть рекомендации по совершенствованию модели? * Промежуточные таблицы и расчеты, аналогичные рассмотренным в гл. 2, здесь не приводятся. * Взвешенный метод наименьших квадратов (ВМНК) рассмотрен в гл. 5. * Авторегрессионные модели будут рассмотрены в следующей главе 6.
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.233.198 (0.01 с.) |

 ,
,  ,
,  и с учетом (5.16) получим:
и с учетом (5.16) получим: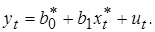 (5.20)
(5.20)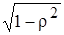 . Тогда с учетом поправки Прайса-Уинстона имеем:
. Тогда с учетом поправки Прайса-Уинстона имеем:

 . (5.22)
. (5.22) , можно выписать ковариационную матрицу случайного вектора e для обобщенной модели с автокоррелируемыми остатками:
, можно выписать ковариационную матрицу случайного вектора e для обобщенной модели с автокоррелируемыми остатками: .
. оказывается значимой, то ее можно использовать в вышеприведенных преобразованиях.
оказывается значимой, то ее можно использовать в вышеприведенных преобразованиях. . (5.23)
. (5.23)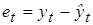 отклонений e t.
отклонений e t. . (5.24)
. (5.24) и
и  .
. и
и  оцениваемой по ежегодным данным (1971-1998 гг.), получены следующие результаты: сумма квадратов остатков для данных 1971-1980 гг. равна
оцениваемой по ежегодным данным (1971-1998 гг.), получены следующие результаты: сумма квадратов остатков для данных 1971-1980 гг. равна 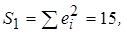 для данных 1989-1998 гг. эта сумма равна
для данных 1989-1998 гг. эта сумма равна 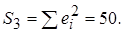 С помощью теста Голдфелда-Квандта проверьте предположение об отсутствии гетероскедастичности.
С помощью теста Голдфелда-Квандта проверьте предположение об отсутствии гетероскедастичности.


