
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка значимости уравнения множественной регрессии в целом. Частные F-критерии Фишера.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера:
Dост - остаточная сумма квадратов на одну степень свободы; R2 - коэффициент (индекс) множественной детерминации; m – число параметров при переменных х n – число наблюдений. Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. Предположим, что оцениваем значимость влияния х1 как дополнительно включенного в модель фактора. Используем следующую формулу:
n – число наблюдений m – число параметров в модели (без свободного члена). Если оцениваем значимость влияния фактора хn после включения в модель факторов x1,x2, …,xn-1, то формула частного F-критерия определится как
В общем виде для фактора xi частный F-критерий Фишера определится как
Фактическое значение F-критерия Фишера сравнивается с табличным при 5%-ном или 1%-ном уровне значимости и числе степеней свободы: m и n-m-1. Если Fфакт>Fтабл(a,n,n-m-1), то дополнительное включение фактора xi в модель статистически оправданно и коэффициент чистой регрессии bi при факторе xi статистически значим. Если же Fфакт<Fтабл(a,n,n-m-1), то дополнительное включение фактора xi в модель существенно не увеличивает долю объясненной вариации признака y, следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим. С помощью частного F-критерия Фишера можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор xi вводился в уравнение множественной регрессии последним. Если уравнение содержит больше двух факторов, то соответствующая программа ПК дает таблицу дисперсионного анализа, показывая значимость последовательного добавления к уравнению регрессии соответствующего фактора. Так, если рассматривается уравнение y=a+b1x1+b2x2+ b3x3+ε, то определяются последовательно F-критерий для уравнения с одним фактором х1, далее F-критерий для дополнительного включения в модель фактора х2, т.е. для перехода от однофакторного уравнения регрессии к двухфакторному, и, наконец, F-критерий для дополнительного включения в модель фактора х3 после включения в модель фактора х1 и х2. В этом случае F-критерий для дополнительного включения фактора х1 после х2 является последовательным в отличие от F-критерия для дополнительного включения в модель фактора х3, который является частным F-критерием, ибо оценивает значимость фактора в предположении, что он включен в модель последним. Нелинейная регрессия. Корреляция для нелинейной регрессии Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два класса нелинейных регрессий: 1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например – полиномы различных степеней – – равносторонняя гипербола – –полулогарифмическая функция – 2. Регрессии, нелинейные по оцениваемым параметрам, например – степенная – – показательная – – экспоненциальная – - логистическая – - обратная – Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости, дополняется показателем тесноты связи. В данном случае это индекс корреляции:
Так как
Величина данного показателя находится в пределах: 0£r£1. Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.
Фиктивные переменные До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными. Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых уравнение регрессии имеет вид: y=a+bx+e, где y – количество потребляемого кофе; x– цена. Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: y1=a1+b1x1+e1 и женского пола: y2=a2+b2x2+e2. Различия в потреблении кофе проявятся в различии средних y=a1z1+a2z2+bx+e, где z1и z2 – фиктивные переменные, принимающие значения:
В общем уравнении регрессии зависимая переменная y рассматривается как функция не только цены yx, но и пола (z1,z2). Переменная z рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом когда z1=1, то z2=0, и наоборот. Для лиц мужского пола, когда z1=1 и z2=0, объединенное уравнение регрессии составит: Однако при введении двух фиктивных переменных z1 и z2 в модель y=a1z1+a2z2+bx+e применение МНК для оценивания параметров a1 и a2 приведет к вырожденной матрице исходных данных, а следовательно, и к невозможности получения их оценок. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т.е. уравнение примет вид y=A+a1z1+a2z2+bx+e. Предполагая при параметре A независимую переменную, равную 1, имеем следующую матрицу исходных данных:
В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена. Выходом из создавшегося затруднения может явиться переход к уравнениям y=A+A1z1+bx+e или y=A+A2z2+bx+e, т.е. каждое уравнение включает только одну фиктивную переменную z1 или z2. Предположим, что определено уравнение y=A+A1z1+bx+e, где z1 принимает значения 1 для мужчин и 0 для женщин. Теоретические значения размера потребления кофе для мужчин будут получены из уравнения
Для женщин соответствующие значения получим из уравнения
Сопоставляя эти результаты, видим, что различия в уровне потребления мужчин и женщин состоят в различии свободных членов данных уравнений: A– для женщин и A+A1 – для мужчин. Теперь качественный фактор принимает только два состояния, которым соответствуют значения 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели. Мы рассмотрели модели с фиктивными переменными, в которых последние выступают факторами. Может возникнуть необходимость построить модель, в которой дихотомический признак, т.е. признак, который может принимать только два значения, играет роль результата. Подобного вида модели применяются, например, при обработке данных социологических опросов. В качестве зависимой переменной y рассматриваются ответы на вопросы, данные в альтернативной форме: «да» или «нет». Поэтому зависимая переменная имеет два значения: 1, когда имеет место ответ «да», и 0 – во всех остальных случаях. Модель такой зависимой переменной имеет вид: y=a=b1x1+…+bmxm+e Модель является вероятностной линейной моделью. В ней y принимает значения 1 и 0, которым соответствуют вероятности p и 1-p. Поэтому при решении модели находят оценку условной вероятности события y при фиксированных значениях x. Для оценки параметров линейно-вероятностной модели применяются методы Logit-, Probit- и Tobit-анализа. Такого рода модели используют при работе с неколичественными переменными. Как правило, это модели выбора из заданного набора альтернатив. Зависимая переменная y представлена дискретными значениями (набор альтернатив), объясняющие переменные xi – характеристики альтернатив (время, цена), zj – характеристики индивидов (возраст, доход, уровень образования). Модель такого рода позволяет предсказать долю индивидов в генеральной совокупности, которые выбирают данную альтернативу. Среди моделей с фиктивными переменными наибольшими прогностическими возможностями обладают модели, в которых зависимая переменная y рассматривается как функция ряда экономических факторов xi и фиктивных переменных zj. Последние обычно отражают различия в формировании результативного признака по отдельным группам единиц совокупности, т.е. в результате неоднородной структуры пространственного или временного характера.
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1660; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 , где Dфакт - факторная сумма квадратов на одну степень свободы;
, где Dфакт - факторная сумма квадратов на одну степень свободы; , где
, где  - коэффициент множественной детерминации для модели с полным набором факторов;
- коэффициент множественной детерминации для модели с полным набором факторов; - тот же показатель, но без включения в модель фактора х1;
- тот же показатель, но без включения в модель фактора х1;



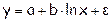 .
. ;
; ;
;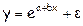 .
. ,
, .
.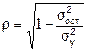 , где
, где  – общая дисперсия результативного признака y,
– общая дисперсия результативного признака y, – остаточная дисперсия.
– остаточная дисперсия.
 и
и 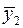 . Вместе с тем сила влияния x на x может быть одинаковой, т.е. b»b1»b2. В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения y1 и y2 и, вводя фиктивные переменные, можно прийти к следующему выражению:
. Вместе с тем сила влияния x на x может быть одинаковой, т.е. b»b1»b2. В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения y1 и y2 и, вводя фиктивные переменные, можно прийти к следующему выражению: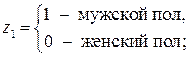
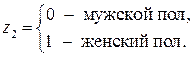
 , а для лиц женского пола, когда z1=0 и z2=1:
, а для лиц женского пола, когда z1=0 и z2=1:  . Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: a1¹a2. Параметр b является общим для всей совокупности лиц, как для мужчин, так и для женщин.
. Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: a1¹a2. Параметр b является общим для всей совокупности лиц, как для мужчин, так и для женщин. .
. .
. .
.


