
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение уравнения регрессии в стандартизованном масштабе.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
b1,b2-коэффициенты регрессии, абсолютные показатели силы связи. По абсолютным показателям силы связи нельзя сравнивать факторы, т.е.делать вывод, какой фактор более сильно влияет на результат. Для этой цели используются относительные показатели силы связи или стандартизированные коэффициенты регрессии(бета коэффициенты). Представим наше уравнение в натуральном масштабе, т.е. с натуральными измерителями. Для этого нужно выразить в стандартных,единых измерителях- сигма(стандартное отклонение):
Запишем уравнение в стандартизированном виде:
К этому уравнению можно применить МНК. Можно записать систему уравнений. ryx1=β1+β2rx2x1+β3rx3x1+βprxpx1 ryx2= β2rx2x1+β2+β3rx3x2+βprxpx2 ryxp= β2rxpx1+β3rxpx2+βprx3xp+βp
По бетта коэффициентам можно сравнивать факторы по силе влияния их на результат. Параметр а определяется как а=ӯ-b1Х1ср-b2X2ср-…-bpXpср Средние коэф эластичности Частные коэф эластичности Эухj=bj(xj / ŷxj*x1,x2, ….,xj-1,xj+1,…xp) Тесноту совместного влияния факторов на результат оценивает ндекс множественной корреляции или в стандартизованном виде:
Значение индекса лежит в пределах от 0 до 1 и д/б больше или равно максимальному парному индексу корреляции (ryxj)
Абсолютные и относительные показатели силы связи в модели множественной регрессии. Абсолютные - показывают, на сколько единиц в среднем изменяется результативный признак при изменении рассматриваемого факторного признака на одну единицу при условии, что остальные факторы зафиксированы на среднем уровне и не меняются.(b-параметры в уравнении) Относительны е: · частные коэф эластичности; показывают, на сколько процентов в среднем меняется результативный признак при изменении рассматриваемого факторного признака на один процент при условии, что остальные факторы зафиксированы на среднем уровне и не меняются. Параметры · стандартизованные коэффициенты регрессии Множественный коэффициент корреляции и коэффициент детерминации. Коэффициент множественной детерминации (R²) показывает долю вариации результативного признака, за счет вариации включенных в модель факторов. Используется для сравнения моделей, это важнейший показатель качества модели.:
Для сравнения модели с разным набором факторов и полученных на основе различного числа наблюдений используют скорректированный коэффициент детерминации.
Коэффициент (индекс) множественной корреляции (R) – корень квадратный из коэффициента множественной детерминации
22. Показатели частной корреляции. Основаны на соотношении сокращения остаточной вариации за счет дополнительно включенного в модель фактора к остаточной вариации до включения в модель соответствующего фактора
Рассмотренные показатели можно также использовать для сравнения факторов, т.е. Можно ранжировать факторы(т.е.2ой фактор более тесно связан). Частные коэффициенты могут быть использованы в процедуре отсева факторов при построении модели. Рассмотренные выше показатели являются коэф-ми корреляции первого порядка,т.е.они характризуют связь между двумя факторами при закреплении одного фактора (yx1. x2). Однако можно построить коэф-ты 2го и более порядка (yx1. x2x3, yx1. x2x3x4). Оценка значимости уравнения регрессии и его параметров Проверка достоверности всего уравнения:
Таблица дисперсионного анализа
Оценка достоверности параметров
где
Уравнение значимо, если оно достоверно по F-критерию и значимы все его параметры. Можно построить доверительный интервал для оценивания параметров.
Частные F-критерии По уравнению множественно регрессии оценивается значимость не только модели в целом, но и значимость дополнительного включения в модель соответствующего фактора. Необходимость такой оценки связана с тем, что не каждый фактор, входящий в модель может существенно увеличить факторную вариацию. Кроме того в виду корреляции между факторами, значимость одного и того же фактора может быть различной в зависимости от последовательности включения в модель этого фактора.
SSe(1)остаточная сумма квадратов для модели без фактора xj SSe(2) - остаточная сумма квадратов для модели с фактором xj
Если Fфакт> Fтаб, то С вероятностью 0,95 можно утверждать, что включения фактора x1 после x2 целесообразно. Fj= tb(j)^2 Можно построить частные таблицы дисперсионного анализа:
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 995; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |




 Связь множественной регрессии b со стандартизованными коэф β описывается соотношением
Связь множественной регрессии b со стандартизованными коэф β описывается соотношением

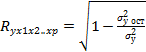


 в степенной модели являются частными коэффициентами эластичности.
в степенной модели являются частными коэффициентами эластичности. .
.

 :
:







 ,
, - случайная ошибка коэффициента условно чистой регрессии
- случайная ошибка коэффициента условно чистой регрессии 

 Мерой для оценки целесообразности включения фактора в модель служит частный F-критерий. Частный F-критерий строится на сравнении пироста факторной дисперсии (на 1 степень свободы), обусловленный влиянием дополнительно включенного в модель фактора к остаточной дисперсии на 1 ст свободы по регрессионной модели.
Мерой для оценки целесообразности включения фактора в модель служит частный F-критерий. Частный F-критерий строится на сравнении пироста факторной дисперсии (на 1 степень свободы), обусловленный влиянием дополнительно включенного в модель фактора к остаточной дисперсии на 1 ст свободы по регрессионной модели.
 - прирост степеней свободы (=1 при добавлении 1 фактора)
- прирост степеней свободы (=1 при добавлении 1 фактора)


