
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о корреляционном и регрессивном анализеСодержание книги
Поиск на нашем сайте Существуют два вида зависимостей: функциональная и стохастическая (вероятностная). Функциональная: каждому значению одной переменной соответствует одно, определённое значение другой. Пример 12. 1) 2) Строгая функциональная зависимость между случайными величинами на практике встречается редко. Гораздо чаще другая, когда каждому численному значению одной случайной величины не соответствует одно, определённое значение другой. Пример 13. Между ростом Х и весом Y человека (наугад выбранного) имеется зависимость, но она не является функциональной. Связь между случайными величинами, имеющими общие случайные факторы, которые влияют как на одну, так и на другую случайную величину, наряду с другими, неодинаковыми для обеих случайных величин факторами, называется стохастической. В статистике её называют статистической.
: Определение. Статистической называют зависимость, при которой изменение одной случайной величины влечёт изменение распределения другой. На рис. 8 приведены примеры функциональной и статистической зависимостей.

Рис. 8
Исследование взаимозависимости случайных величин рассматривается в корреляционном анализе (зависимость веса Y от роста Х – корреляционная зависимость). Исследование зависимости случайной величины от ряда неслучайных и случайных величин рассматривается в регрессионном анализе (зависимость между урожайностью сельскохозяйственных культур от природных и экономических факторов). В корреляционном анализе оценивается сила стохастической связи, в регрессионном – исследуется её форма.
: Определение. Условной средней
Пример 14. При х = 2 Y приняла значения: 5, 6, 10, тогда : Определение. Корреляционной зависимостью Y от Х называют функциональную зависимость условной средней
Это уравнение регрессии Y на Х. Функцию f(x) называют регрессией Y на Х, а её график – линией регрессии Y на Х. Аналогично: условная средняя Уравнение регрессии Х на Y:
где j(y) – регрессия Х на Y. Чаще всего теоретические регрессии (16) и (17) неизвестны, и их оценивают при помощи эмпирических регрессий. Экспериментальные данные
Аналогично В зависимости от числа случайных величин различают простую и множественную регрессии. Пример 15. 1. Простая регрессия – регрессия между затратами на производстве и объёмом продукции, производимой предприятием. 2. Множественная регрессия – регрессия между производительностью труда и уровнем механизации производственных процессов, фондом рабочего времени, материалоёмкостью, квалификацией рабочих. По форме различают линейную и нелинейную регрессии. Линейная регрессия:
где Обе линии регрессии Y на Х и Х на Y – прямые. Выборочное уравнение прямой линии регрессии Y на Х имеет вид:
где
где x, y – варианты;
Аналогично определяется выборочное уравнение прямой линии регрессии Х на Y:
Связь коэффициентов регрессии и коэффициентов корреляции:
Если Выборочный коэффициент корреляции служит для оценки тесноты линейной корреляционной зависимости. Свойства выборочного коэффициента корреляции 1. | 2. Если 3. Если | 4. С возрастанием | при | при | Пример 16 (из тестов). 1. При построении уравнения парной регрессии y = α + βx + ξ были получены результаты: -3; 0,6; -0,6; 2. Решение.
Ответ: 0,6. 2. Выборочное уравнение парной регрессии имеет вид y = –3 + 2 x. Тогда выборочный коэффициент корреляции может быть равен… -3; 0,6; -0,6; 2. Решение. |
|
||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1943; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.007 с.) |



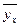 называют среднее арифметическое значение Y, соответствующее значению Х = х.
называют среднее арифметическое значение Y, соответствующее значению Х = х. .
. от х:
от х: .(16)
.(16) равна среднему арифметическому значений Х, соответствующих Y = у.
равна среднему арифметическому значений Х, соответствующих Y = у. (17)
(17) изображают в виде точек в декартовой системе координат. Исходя из характера расположения точек выбирают вид функции регрессии и её оценки, т.е. эмпирической регрессии (прямая, парабола и т.д.):
изображают в виде точек в декартовой системе координат. Исходя из характера расположения точек выбирают вид функции регрессии и её оценки, т.е. эмпирической регрессии (прямая, парабола и т.д.): – эмпирическое уравнение Y на Х. Параметры
– эмпирическое уравнение Y на Х. Параметры  находят методом наименьших квадратов.
находят методом наименьших квадратов.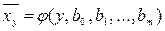 .
. ,
, ,
, коэффициенты регрессии.
коэффициенты регрессии.
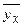 – условная средняя;
– условная средняя; – выборочные средние Х и Y;
– выборочные средние Х и Y;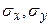 – выборочные средние квадратические отклонения;
– выборочные средние квадратические отклонения; – выборочный коэффициент корреляции.
– выборочный коэффициент корреляции. ,
, – частота пары вариант (x, y);
– частота пары вариант (x, y); – объём выборки (сумма всех частот);
– объём выборки (сумма всех частот); – коэффициент регрессии.
– коэффициент регрессии. .
. ;
;  ;
;  .
. ,
,  , то Х и Y одновременно возрастают, если
, то Х и Y одновременно возрастают, если 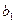 < 0,
< 0,  < 0, то X и Y убывают. Чем меньше угол между прямыми регрессии Y на Х и Х на У, тем теснее связь между Х и Y.
< 0, то X и Y убывают. Чем меньше угол между прямыми регрессии Y на Х и Х на У, тем теснее связь между Х и Y. :
: = 2;
= 2;  = 1,5, тогда коэффициент регрессии β равен:
= 1,5, тогда коэффициент регрессии β равен: .
. |≤ 1 (всегда),
|≤ 1 (всегда),  = 2 (из условия),
= 2 (из условия),  (всегда), следовательно,
(всегда), следовательно, 


