
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи математической статистикиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте ТЕОРИЯ И ПРАКТИКА
Рекомендовано редакционно-издательским советом университета в качестве учебного пособия для студентов специальностей 220301, 230104, 230201 очной формы обучения
Кострома ИЗДАТЕЛЬСТВО
ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Математические законы теории вероятностей не являются абстрактными, лишёнными физического содержания, они представляют собой математическое выражение реальных закономерностей, существующих в массовых случайных явлениях. Каждое исследование случайных явлений, выполняемое методами теории вероятностей, опирается на экспериментальные данные. Зарождение математической статистики было связано со сбором данных и графическим представлением полученных результатов (сводки рождаемости, бракосочетаний и т.д.). Это описательная статистика. Нужно было свести обширный материал к небольшому числу величин. Разработка методов сбора (регистрации), описания и анализа экспериментальных (статистических) данных, получаемых в результате наблюдения массовых, случайных явлений, составляет предмет математической статистики. При этом можно выделить три этапа: 1) сбор данных; 2) обработка данных; 3) статистические выводы-прогнозы и решения. Типичные задачи математической статистики: - определение закона распределения случайной величины (или системы случайных величин) по статистическим данным; - проверка правдоподобия гипотез; - нахождение неизвестных параметров распределения. Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
ГЕНЕРАЛЬНАЯ И ВЫБОРОЧНАЯ СОВОКУПНОСТЬ. СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ВЫБОРКИ. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ РАСПРЕДЕЛЕНИЙ Пусть требуется изучить статистическую совокупность относительно некоторого количественного признака X. Числовые значения признака будем обозначать через хi. Из генеральной совокупности извлекается выборка объёма п. I. Количественный признак Х – дискретная случайная величина. Наблюдаемые значения хi называют вариантами, а последовательность вариантов, записанных в возрастающем порядке, – вариационным рядом. Пусть x1 наблюдалось n1 раз, x2 наблюдалось n2 раз, xk наблюдалось nk раз, причем Значение вариант и соответствующие им частоты или относительные частоты можно записать в виде таблиц 1 и 2. Таблица 1
Таблицу 1 называют дискретным статистическим рядом распределения (ДСР) частот, или таблицей частот. Таблица 2
Таблица 2 - ДСР относительных частот, или таблица относительных частот. : Определение. Модой называется наиболее часто встречающийся вариант, т.е. вариант с наибольшей частотой. Обозначается xмод .
: Определение. Медианой называется такое значение признака, которое делит всю статистическую совокупность, представленную в виде вариационного ряда, на две равных по числу части. Обозначается Если n нечетно, т.е. n = 2m + 1, то Если n четно, т.е. n = 2m, то
Пример 3. По результатам наблюдений: 1, 7, 7, 2, 3, 2, 5, 5, 4, 6, 3, 4, 3, 5, 6, 6, 5, 5, 4, 4 построить ДСР относительных частот. Найти моду и медиану. Решение. Объем выборки n = 20. Составим ранжированный ряд элементов выборки: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 7, 7. Выделим варианты и подсчитаем их частоты (в скобках): 1 (1), 2 (2), 3 (3),
Наиболее часто встречающийся вариант xi = 5. Следовательно, xмод = 5. Так как объем выборки n – четное число, то Если на плоскости нанести точки Если на плоскости нанести точки Пример 4. Построить полигон частот и полигон относительных частот по данному распределению выборки:
Решение. На рисунке 2 показан полигон частот и на рисунке 3 – полигон относительных частот.
Рис. 2 Рис. 3 Замечание. Чем круче полигон, тем равномернее процесс.
II. Пусть количественный признак X – непрерывная случайная величина, принимающая значения из интервала (а,b). Весь диапазон наблюдаемых данных делят на частичные интервалы [ хi; xi+1), которые берут обычно одинаковыми по длине:
где (xmax – xmin)- разность между наибольшим и наименьшим значениями признака, k = 1 + log2 n - число интервалов (log2 n» 3,322 lg n). Если окажется, что h - дробное число, то за длину частичного интервала следует брать либо ближайшее целое число, либо ближайшую простую дробь. За начало первого интервала рекомендуется брать величину x нач = x min – Таблица 3
Таблица 3 называется интервальным статистическим рядом распределения (ИСР) относительных частот, который задаёт распределение выборки. Аналогично составляется ИСР частот. Пример 5. Измерили рост (с точностью до см) 30 наудачу отобранных студентов. Результаты измерений таковы: 178, 160, 154, 183, 155, 153, 167, 186, 163, 155, 157, 175, 170, 166, 159, 173, 182, 167, 171, 169, 179, 165, 156, 179, 158, 171, 175, 173, 164, 172. Построить интервальный статистический ряд относительных частот. Решение. Для удобства проранжируем полученные данные: 153, 154, 155, 155, 156, 157, 158, 159, 160, 163, 164, 165, 166, 167, 167, 169, 170, 171, 171, 172, 173, 173, 175, 175, 178, 179, 179, 182, 183, 186. Отметим, что Х - рост студента - непрерывная случайная величина. Как видим, xmin = 153, хmax = 186; по формуле Стерджеса, при n = 30, находим длину частичного интервала
Примем [150, 156), [156, 162), [162, 168), [168, 174), [174, 180), [180, 186]. Подсчитав число студентов ni, попавших в каждый из полученных промежутков, получим ИСР:
Первая и третья строчка таблицы образует ИСР относительных частот. Замечание. При решении учебных задач на построение ИСР можно пользоваться следующими правилами. 1. Назначаются нижняя граница а и верхняя граница b для вариант так, чтобы отрезок [ a; b ] вместил всю выборку; часто полагают 2. Находится число k равных по длине частичных интервалов варьирования, которое зависит от объема выборки и обычно 6 £ k £ 20; рассчитывается длина интервалов группирования Интервальный статистический ряд распределения, представленный графически, называется гистограммой. Гистограмма относительных частот строится следующим образом: по оси абсцисс откладываются интервалы (хi; хi+1) и на каждом из них строится прямоугольник высотой
Площадь i- го прямоугольника Площадь всей гистограммы
Рис. 4 Можно построить гистограмму частот, высоты прямоугольников которых равны Пример 6. Построить гистограмму частот по данному ИСР частот:
Решение. По ИСР частот находим длину частичных интервалов
Искомая гистограмма частот изображена на рис. 5.

Рис. 5
В теории вероятностей гистограмме относительных частот соответствует график плотности распределения вероятностей. Распределение выборки, задаваемое интервальным статистическим рядом (табл. 3) или таблицей относительных частот (табл. 2), называется эмпирическим распределением случайной величины. По теореме Бернулли относительная частота wi, появление события в п независимых испытаниях сходится по вероятности к вероятности рi этого события Замечания. 1. Выборочные средние, найденные по нескольким выборкам достаточно большого объёма из некоторой генеральной совокупности, приближенно равны между собой. 2. Предполагали, что выборка повторная. Однако полученные выводы применимы и для бесповторной выборки, если её объём значительно меньше объема генеральной совокупности. 3. Эффективность или неэффективность зависит от вида закона распределения признака X. Если X распределена по нормальному закону, то
Решение.
Если, например, Смысл результата: если произведено достаточно большое число выборок, то 95% из них определяют такие доверительные интервалы, в которых неизвестное математическое ожидание а действительно заключено. Лишь в 5% случаев а может выйти за границы доверительного интервала. Вычисление объема выборки при заданных Пусть требуется оценить математическое ожидание, если заданы доверительная вероятность Точность оценки Значит, Замечание. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном X – количественный признак, распределён нормально. a, Требуется оценить a. Можно доказать, что Решение.
Ответ: 0,6. 2. Выборочное уравнение парной регрессии имеет вид y = –3 + 2 x. Тогда выборочный коэффициент корреляции может быть равен… -3; 0,6; -0,6; 2. Решение. | ТЕОРИЯ И ПРАКТИКА
Рекомендовано редакционно-издательским советом университета в качестве учебного пособия для студентов специальностей 220301, 230104, 230201 очной формы обучения
Кострома ИЗДАТЕЛЬСТВО
ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Математические законы теории вероятностей не являются абстрактными, лишёнными физического содержания, они представляют собой математическое выражение реальных закономерностей, существующих в массовых случайных явлениях. Каждое исследование случайных явлений, выполняемое методами теории вероятностей, опирается на экспериментальные данные. Зарождение математической статистики было связано со сбором данных и графическим представлением полученных результатов (сводки рождаемости, бракосочетаний и т.д.). Это описательная статистика. Нужно было свести обширный материал к небольшому числу величин. Разработка методов сбора (регистрации), описания и анализа экспериментальных (статистических) данных, получаемых в результате наблюдения массовых, случайных явлений, составляет предмет математической статистики. При этом можно выделить три этапа: 1) сбор данных; 2) обработка данных; 3) статистические выводы-прогнозы и решения. Типичные задачи математической статистики: - определение закона распределения случайной величины (или системы случайных величин) по статистическим данным; - проверка правдоподобия гипотез; - нахождение неизвестных параметров распределения. Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.012 с.) |

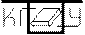
 . Числа ni называют частотами, а их отношение к объёму выборки, т.е.
. Числа ni называют частотами, а их отношение к объёму выборки, т.е.  , – относительными частотами (или частостями), причем
, – относительными частотами (или частостями), причем  .
. .
.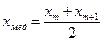 .
.
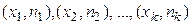 и соединить их отрезками прямых, то получим полигон частот.
и соединить их отрезками прямых, то получим полигон частот. , то получим полигон относительных частот.
, то получим полигон относительных частот.

 = xi+1 – xi (i = 0, 1, …, k). Для определения величины интервала
= xi+1 – xi (i = 0, 1, …, k). Для определения величины интервала 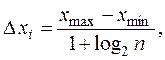
 . В каждом из частичных интервалов подсчитывают число наблюдаемых значений, т.е. частоту ni. По частотам находят относительные частоты
. В каждом из частичных интервалов подсчитывают число наблюдаемых значений, т.е. частоту ni. По частотам находят относительные частоты  . Полученные интервалы и соответствующие им частоты (или относительные частоты) записывают в виде таблицы 3. При этом правая граница последнего интервала тоже включается.
. Полученные интервалы и соответствующие им частоты (или относительные частоты) записывают в виде таблицы 3. При этом правая граница последнего интервала тоже включается.
 = 6. Тогда хнач = 153 –
= 6. Тогда хнач = 153 –  =150. Исходные данные разбиваем на шесть (k = 1 + log230 = 5,907» 6) интервалов:
=150. Исходные данные разбиваем на шесть (k = 1 + log230 = 5,907» 6) интервалов: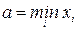 ,
,  , но иногда a и b назначают из соображений удобства, но не слишком далеко от
, но иногда a и b назначают из соображений удобства, но не слишком далеко от 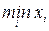 и
и  .
. .
.
 ;
;  .
. .
. .
. Замечание: гистограмма на рисунке 4 – гистограмма относительных частот.
Замечание: гистограмма на рисунке 4 – гистограмма относительных частот.
 .
.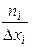 . Результаты занесем в таблицу:
. Результаты занесем в таблицу: . Значит во второй строке таблицы 3 и таблицы 2 стоят приближённые значения вероятностей рi следующих событий
. Значит во второй строке таблицы 3 и таблицы 2 стоят приближённые значения вероятностей рi следующих событий  и
и  , поэтому распределение выборки называют эмпирическим распределением случайной величины X.
, поэтому распределение выборки называют эмпирическим распределением случайной величины X. будет минимально возможной, т.е. средняя выборочная является эффективной оценкой.
будет минимально возможной, т.е. средняя выборочная является эффективной оценкой. ;
;  .
. 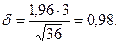
 – доверительный интервал.
– доверительный интервал. , то (3,12; 5,08).
, то (3,12; 5,08). и
и 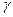
 . Тогда
. Тогда  .
.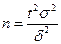 – минимальный объем выборки, который обеспечит заданную точность
– минимальный объем выборки, который обеспечит заданную точность  .
. - доверительный интервал, покрывающий неизвестное математическое ожидание a с доверительной вероятностью
- доверительный интервал, покрывающий неизвестное математическое ожидание a с доверительной вероятностью  – выборочная средняя;
– выборочная средняя;  – исправленное среднее квадратическое отклонение;
– исправленное среднее квадратическое отклонение;  – квантиль распределения, который находят по таблице 3 по заданным
– квантиль распределения, который находят по таблице 3 по заданным  и
и  .
. |≤ 1 (всегда),
|≤ 1 (всегда),  = 2 (из условия),
= 2 (из условия),  (всегда), следовательно,
(всегда), следовательно,  = 0,6.
= 0,6.


