
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра статистики и прикладной математикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное образовательное учреждение высшего профессионального образования «КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ» УЧЕТНО-ФИНАНСОВЫЙ ФАКУЛЬТЕТ КАФЕДРА СТАТИСТИКИ И ПРИКЛАДНОЙ МАТЕМАТИКИ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ЗАДАЧИ И УПРАЖНЕНИЯ
КРАСНОДАР – 2009
Задания предназначены для закрепления теоретических знаний, полученных на лекциях, при самостоятельном изучении учебников и учебных пособий студентами экономических специальностей. Содержание и тематика заданий соответствует действующей программе по теории вероятностей и математической статистике. Отдельные задачи носят условный характер, значительная часть составлена по реальным данным организаций Краснодарского края. По каждой теме предусмотрено решение студентами индивидуальных заданий с последующей их сдачей преподавателю. Задания разработаны профессорами Бондаренко П.С., Кацко И.А., ст. преподавателями Гумбаровой Л.А., Стеганцовой Е.Д., Чернобыльской Т.Ю. Задания рассмотрены и рекомендованы к печати кафедрой статистики и прикладной математики КубГАУ (протокол № 12 от 21 июня 2009 г) и методической комиссией учетно-финансового факультета (протокол № 11 от 25 июня 2009 г)
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Гмурман В.Е.Теория вероятностей и математическая статистика. Изд. 12-е, перераб. – М.: Высшая школа, 2006. – 479 с. 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебное пособие.- 10-е изд. – М.: Высшая школа, 2006. 3. Горелова Г.В., Кацко И.А. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel. 4. Колемаев В.А., Калинина В.И. Теория вероятностей и математическая статистика. М.: ИНФРА – М, 1997-302 с. 5. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник. 6. Теория статистики с основами теории вероятностей. /И.И. Елисеева, В.С. Князевский, Л.И. Новорожкина, З.А. Морозова; Под ред. И.И.Елисеевой. – М.: ЮНИТИ –ДАНА, 2001. – 446 с. 7. Фадеева Л.Н., Жуков Ю.В., Лебедев А.В. Математика для экономистов. Теория вероятностей и математическая статистика. Задачи и упражнения. – М.: ЭКСМО, 2007. – 336 с.
СОДЕРЖАНИЕ
СЛУЧАЙНЫЕ СОБЫТИЯ Событие есть возможный результат опыта или испытания. Достоверным называется событие U, которое в данном опыте обязательно произойдет. Невозможным называется событие V, которое в данном опыте не может произойти. Случайным называется событие А, которое в данном опыте или испытании может произойти, а может и не произойти. События называются совместными, если появление одного из них не исключает появление других в данном опыте. Если два события не могут появиться в одном опыте, то они называются несовместными. Несколько событий называются попарно-несовместными, если никакие два из них не могут появиться вместе в данном опыте. Если события попарно-несовместные и какое-либо из них обязательно появится в опыте, то они образуют полную группу событий. События являются равновозможными, если ни одно из них не имеет преимущества на наступление перед другими.
Вероятность события А обозначается Р(А) и находится по формуле:
где
Вероятность любого события А заключена между нулем и единицей,
При определении вероятностей событий часто используются формулы комбинаторики, позволяющие подсчитать число различных способов выбора - число размещений из
- число перестановок из
- число сочетаний из
Различные размещения отличаются друг от друга или порядком или составом. Различные сочетания отличаются друг от друга только составом. Перестановки отличаются порядком своих элементов. Число перестановок, размещений и сочетаний с возвращениями определяется по формулам:
Относительной частотой или статистической вероятностью события А называется число исходов, в которых появилось событие А к общему числу проведенных исходов.
Если число элементарных исходов бесконечно, то используют геометрическое определение вероятности. Вероятность попадания точки в область
1 Являются ли несовместными следующие события: а) Опыт - бросание двух монет; события: А1 – появление двух гербов; А2 – появление двух цифр. б) Опыт – три выстрела по мишени; события: В1 – хотя бы одно попадание; В2 – хотя бы один промах. в) Опыт – бросание двух игральных костей; события: С1 – хотя бы на одной кости появилось три очка; С2 – появление четного числа очков на каждой кости. г) Опыт – извлечение двух шаров из урны, содержащей белые и черные шары; события: Д1 – взято два белых шара; Д2 – оба извлеченных шара одного цвета. д) Опыт – студент сдает три экзамена, события: Е1 – студент сдает хотя бы один экзамен; Е2 – студен не сдает хотя бы один экзамен; е) Опыт – лифт отправляется с 10 пассажирами и останавливается на пяти этажах; события: F1 – на первых четырех остановках вышло не более 9 человек; F2 – на последней остановке вышел хотя бы один человек. 2 Образуют ли полную группу следующие события: а) Опыт – два выстрела по мишени; события: А1 – два попадания в мишень; А2 – хотя бы один промах по мишени. б) Опыт – бросание двух игральных костей; события: В1 – сумма очков на верхних гранях больше 3; В2 – сумма очков на верхних гранях равна 3. в) Опыт – посажено четыре зерна; события: С1 – взошло одно зерно; С2 – взошло два зерна; С3 – взошло три зерна; С4 – взошло четыре зерна. г) Покупатель посещает три магазина; события: Д1 – покупатель купит товар хотя бы в одном магазине; Д2 – покупатель не купит товар ни в одном магазине. д) Опыт – студент сдает три экзамена; события: Е1 – студент сдаст хотя бы один экзамен; Е2 – студент не сдаст хотя бы один экзамен. 3 Являются ли равновозможными следующие события: а) Опыт – выстрел по мишени; события: А1 – попадание при выстреле; А2 – промах при выстреле. б) Опыт – бросание двух игральных костей; события: В1 – произведение очков на верхних гранях равно 12;
В2 – сумма очков на верхних гранях равна 9. в) Бросание двух монет; события: С1 – появление двух гербов; С2 – появление двух цифр; С3 – появление одного герба и одной цифры. г) Опыт – извлечение двух карт из колоды; события: Д1 – обе карты одинаковой масти; Д2 – обе карты разных мастей. 4 Брошены 3 монеты. Составить события, образующие полную группу. Сколько равновозможных исходов образует полную группу событий? Укажите события единственно – возможные, не образующие полной группы событий? 5 Приведите примеры: а) трех событий, образующих полную группу событий; б) трех событий, равновозможных и несовместных, но не образующих полной группы событий; в) двух событий, несовместных и образующих полную группу событий, но не равновозможных. 6 Брошена игральная кость. Найти вероятность того, что на ее верхней грани появится: а) шесть очков; б) нечетное количество очков; в) не менее четырех очков; г) не более двух очков; д) более трех очков. 7 Набирая номер телефона, абонент забыл две цифры и, помня лишь, что они различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры. 8 Брошены две игральные кости. Найти вероятность того, что: а) на обеих костях появится одинаковое число очков; б) хотя бы на одной кости появится два очка; в) сумма выпавших очков равна пяти, а произведение шести очкам; г) сумма очков, выпавших на обеих костях, не превзойдет 5. 9 Из 10150 человек, проживающих в населенном пункте, 71 человек имеет возраст свыше 80 лет. Определить статистическую вероятность появления лиц с возрастом свыше 80 лет. Какой процент лиц, имеет возраст до 80 лет? 10 Относительная частота (частость) работников предприятия, имеющих высшее образование, равна 0.15. Определить: а) число работников, имеющих высшее образование, если всего на предприятии работает 40 человек; б) число работников предприятия, если с высшим образованием работает 30 человек. 11 Имеются две урны. В первой – 10 красных и 6 черных шаров. Во второй – 4 красных и 6 черных шаров. Из каждой урны вынимается по шару. Найти вероятность того, что: а) оба шара будут красными; б) из первой урны будет вынут красный шар, а из второй – черный; в) хотя бы один из вынутых шаров черный. 12 Из коробки, содержащей 5 пронумерованных жетонов, вынимают один за другим все находящиеся в ней жетоны и укладывают рядом. Найти вероятность того, что номера вынутых жетонов будут идти по порядку 1, 2, 3, 4, 5. 13 Из пяти букв разрезной азбуки составлено слово «книга». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово «книга».
14 В колоде 36 карт четырех мастей. После извлечения и возвращения одной карты, колода перемешивается и снова извлекается одна карта. Определить вероятность того, что обе извлеченные карты одной масти. 15 На отдельных одинаковых карточках написаны цифры: 1, 2, 3, 4, 5, 6, 7, 8, 9. Все девять карточек перемешивают, после чего наугад берут четыре карточки и раскладывают в ряд в порядке появления. Какова вероятность получить при этом: а) четное число; б) число 1234; в) 6789? 16 Какова вероятность, что на трех карточках, вынутых по одной и положенных в порядке их появления, получим число 325, если всего карточек было шесть с цифрами 1, 2, 3, 4, 5, 6? 17 Восемь различных книг расставляются наугад на полке. Найти вероятность того, что: а) три определенные книги окажутся поставленными рядом; б) две определенные книги окажутся поставленными рядом. 18 Среди изготовленных 15 деталей имеется 5 нестандартных. Определить вероятность того, что взятые наугад три детали окажутся стандартными. 19 В партии готовой продукции из 10 изделий имеется 7 изделий повышенного качества. Наудачу отбираются шесть изделий. Какова вероятность того, что четыре из них будут повышенного качества? 20 Какова вероятность того, что два определенных студента будут посланы на практику в Лабинск, если предоставлено 6 мест в г. Лабинск, 10 – в г. Анапу и 4 – в г. Тимашевск? 21 Из 25 студентов группы, 12 занимаются научной работой на кафедре бухгалтерского учета, 7 - экономического анализа, остальные – на кафедре статистики. Какова вероятность того, что два случайно отобранных студента занимаются научной работой на кафедре статистики? 22 Собрание, на котором присутствует 25 человек, в том числе 5 женщин, выбирает делегацию из трех человек. Найти вероятность того, что в делегацию войдут: а) две женщины и один мужчина; б) все женщины. 23 Среди 20 студентов группы, в которой 10 девушек, разыгрываются 5 билетов в театр. Определить вероятность того, что среди обладателей билетов окажутся три девушки или две девушки. 24 Определить вероятность того, что участник лотереи «Спортлото – 5 из 36» угадает правильно: а) все 5 номеров; б) 3 номера. 25 Цифровой замок содержит на общей оси 4 диска, каждый из которых разделен на 6 секторов, отмеченных цифрами. Замок открывается в том случае, если диски установлены так, что цифры на них составляют определенное четырехзначное число. Какова вероятность того, что замок откроется, если установить произвольную комбинацию цифр? 26 Устройство состоит из пяти элементов, из которых два изношены. При включении устройства включается случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы. 27 В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия; в) хотя бы одно окрашенное изделие. 28 В квадрат с длиной стороны «а» вписан круг. Наудачу в квадрат бросается точка. Найти вероятность того, что точка попадает в круг.
29 В прямоугольник с вершинами А (1;1), В (1;3), С (4;3), Д (4;1) наудачу брошена точка К (х;у). Найти вероятность того, что координаты этой точки удовлетворяют неравенству 30 В прямоугольник с вершинами А (0;0), В (0;5), С (6;5), Д (6;0) наудачу брошена точка. Найти вероятность того, что координаты этой точки удовлетворяют системе неравенств
ФУНКЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН а) Функция одного случайного аргумента. Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины У, то У называют функцией случайного аргумента Х. У = φ(Х). Пусть аргумент Х Если аргумент Х принимает значение хi с вероятностью Рxi, то случайная величина У принимает значение Пусть аргумент Х – непрерывная случайная величина, заданная плотностью распределения f(x). Если у = φ(х) – дифференцируемая, строго возрастающая или строго убывающая функция, обратная функция которой х = ψ(y), то плотность распределения g(у) случайной величины У находится:
Если функция У = φ(Х) в интервале возможных значений Х не монотонна, то следует разбить этот интервал на такие интервалы, в которых функция φ(х) монотонна, и найти плотности распределения gi(у) для каждого из интервалов монотонности, а затем представить g(у) в виде суммы:
Например, если функция φ(х) монотонна на двух интервалах, в которых соответствующие обратные функции
б) Функция двух случайных аргументов. Если каждой паре возможных значений случайных величин Х и У соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов Х и У.
Если Х и У – дискретные независимые случайные величины, то для того чтобы найти распределение функции Z = X + Y надо найти все возможные значения Если Х и У – непрерывные случайные величины, то плотность распределения g(z) суммы Z = X + Y, при условии, что плотность распределения хотя бы одного из аргументов задана в интервале (- ∞; ∞), находится по формуле:
где f1 и f2 – плотности распределения аргументов Х и У. Если возможные значения аргументов неотрицательны, то плотность распределения g(z) величины Z = X + Y находят по формуле:
Если Х и У – независимые случайные величины, заданные соответствующими плотностями распределения
1. Дискретная случайная величина задана законом распределения:
Найти закон распределения случайной величины У, где: а) У=2Х-1; б) У=Х+5; в) У=Х2-2; г) У=
2. Дискретная случайная величина Х задана законом распределения:
Найти закон распределения случайной величины У, где: а) У=2Х+1; б)У=Х3-1; в) У=Х2; г) У=
3. Дискретная случайная величина Х задана законом распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины У, если: а) У=4Х-4; б) У=Х2.
4. Дискретная случайная величина Х задана законом распределения:
Найти: а) закон распределения случайной величины У=sin2 X; б) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины У. 5. Случайная величина Х равномерно распределена на интервале (2;10). Найти дифференциальную функцию случайной величины: а) Y = 0,5 X – 1; б) Y = X2; в) 6. Случайная величина Х равномерно распределена в интервале (- а) Y = sin X; б) У= cos X. 7. Случайная величина Х распределена нормально с параметрами а = 2, а) У=2Х+6; б) У=Х3. 8. Непрерывная случайная величина Х задана функцией
Найти дифференциальную функцию случайной величины: а) 9. Сторона квадрата Х имеет равномерное распределение на отрезке [1;2]. Найти плотность вероятности площади квадрата. 10. Случайная величина Х распределена по закону Коши:
Найти дифференциальную функцию случайной величины: а) У=Х3; б) У=3Х. 11. Независимые случайные величины Х и У распределены равномерно. Случайная величина Х распределена в интервале (0; 2), а случайная величина У в интервале (0; 10). Найти интегральную и дифференциальную функции случайной величины Z=X+У. Построить графики интегральной и дифференциальной функций случайной величины Z. 12. Случайная величина Х равномерно распределена в интервале (-4; 1), а случайная величина У равномерно распределена в интервале (1; 6). Найти дифференциальную функцию случайной величины Z=X+У и начертить ее график. 13. Независимые случайные величины Х и У заданы дифференциальными функциями:
Найти дифференциальную функцию случайной величины Z=X+У. 14. Независимые случайные величины Х и У распределены по нормальному закону:
Найти дифференциальную функцию случайной величины Z=X+У. Показать, что случайная величина Z распределяется по нормальному закону. 15. Натуральный логарифм некоторой случайной величины Х распределен по нормальному закону с центром рассеивания
ЗАКОН БОЛЬШИХ ЧИСЕЛ
Закон больших чисел представляет собой наиболее общий принцип, в результате которого количественные закономерности, присущие массовым случайным явлениям, отчетливо проявляются при достаточно большом числе наблюдений. Лемма Чебышева. Если все значения случайной величины Х неотрицательны, то вероятность того, что случайная величина Х будет не меньше некоторого числа t > 0 не больше, чем
Неравенство Чебышева. Вероятность того, что абсолютное отклонение случайной величины Х от ее математического ожидания меньше некоторого числа ε > 0, не меньше чем
Теорема Чебышева. Если попарно – независимые случайные величины имеют конечные математические ожидания, дисперсии каждой из случайной величины не превосходят постоянного числа С, то среднее арифметическое этих величин сходится по вероятности к среднему арифметическому их математических ожиданий. Если
Воспользовавшись неравенством Чебышева, получаем
1 Цена акций коммерческой фирмы, реализуемых на фондовом рынке, является случайной величиной, математическое ожидание которой равно 6 тыс. руб. Оценить вероятность того, что в ближайшие сутки цена акций превысит 10 тыс. руб. 2 Количество электроэнергии, потребляемой поселком в течении суток, является случайной величиной, математическое ожидание которой равно 4 тыс. кВт.- ч. Оценить вероятность того, что в ближайшие сутки потребление энергии: а) превысит 8 тыс. кВт.- ч.; б) не превысит 6 тыс. кВт.- ч. 3 Пользуясь неравенством Чебышева, оценить вероятность того, что из посеянных 5000 семян число взошедших окажется от 3750 до 4250, если известно, что М(Х) = 4000. Определить вероятность попадания случайной величины в данный интервал. 4 Вероятность вызревания семян овощной культуры в данной местности составляет 0,8. С помощью неравенства Чебышева оценить вероятность того, что из 1000 растений, число растений с вызревшими семенами составит от 750 до 850. Определить вероятность попадания случайной величины в данный интервал. 5 В организации имеется 100 автомобилей. Вероятность безотказной работы каждого из них в течение определенного времени составляет 0,9. С помощью неравенства Чебышева оценить вероятность того, что: а) отклонение числа безотказно работавших автомобилей за определенный период времени от его математического ожидания не превзойдет по модулю 5; б) отклонение доли безотказно работающих автомобилей от постоянной вероятности 0,9 по модулю будет меньше 0,06. 6 Дискретная случайная величина Х задана законом распределения:
Используя неравенство Чебышева, оценить вероятность того, что
8 Дискретная случайная величина Х задана законом распределения:
Используя неравенство Чебышева, оценить вероятность того, что
9 Случайная величина Х задана дифференциальной функцией:
а) С помощью неравенства Чебышева оценить вероятность того, что 10 Случайная величина задана интегральной функцией:
а) С помощью неравенства Чебышева оценить вероятность того, что
11 Случайная величина задана интегральной функцией
а) используя неравенство Чебышева, оценить вероятность того, что
12 Выборочным способом определяют вес колосьев ячменя. Сколько необходимо отобрать колосьев, чтобы с вероятностью не меньшей 0,99, можно было утверждать, что средний вес случайно отобранных колосьев будет отличаться от среднего веса колосьев во всей партии (принимаемого за математическое ожидание) не более чем на 0,1 г? Установлено, что среднее квадратическое отклонение веса не превышает 0,2 г. 13 Сколько человек необходимо отобрать для определения удельного веса лиц со специальным образованием, чтобы с вероятностью 0,95 можно было утверждать, что отклонение относительной частоты лиц со специальным образованием от их доли, принимаемой за постоянную вероятность, не превышало по модулю 0,04.
Цепи Маркова
Результаты различных экспериментов или испытаний могут быть представлены в виде определенной последовательности букв или цифр, которые рассматриваются как процессы перехода от одного состояния в другое. Можно оценить вероятность такого перехода. Модель случайного процесса объединяет множество состояний и множество вероятностей перехода из одного состояния в другое. Множество (пространство) состояний может быть конечным и бесконечным. Последовательность состояний образует цепь Маркова, если в отдельном испытании система принимает одно из возможных состояний, не зависящее от результатов ранее произведенных испытаний. Вероятность
Вероятность перехода процесса из состояния S
Аналогично получается матрица перехода за три шага
1 Вероятности перехода за один шаг в цепи Маркова задаются матрицей: а) Найти число состояний системы. Построить граф, соответствующий матрице р. 2 Задана матрица вероятностей переходов
Каковы пределы изменений р и S? 3 В урне имеется 5 белых и черных шаров. Из урны случайно извлекается один шар, а обратно в урну возвращается один шар другого цвета. Опыт повто ряется неоднократно. Найти матрицу переходных вероятностей, состояниями которой является количество белых шаров в урне. Найти вероятности перехода за два шага. 4 Игральная кость перекладывается многократно с равной вероятностью случайным образом с одной грани на любую из соседних четырех граней, независимо от исхода предыдущего испытания. К какому пределу стремится при 5 Имеется пять стульев, расположенных один возле другого. Человек пересаживается с одного стула на рядом стоящий, причем эти перемещения определяются бросанием правильной игральной кости. Стулья обозначены буквами А,В,С,Д,Е. Вначале он сидит на среднем стуле С. Если человек сидит на крайнем стуле, то: возвращается на стул С, когда выпадет четное число очков; остается на том же месте при выпадении нечетного числа очков. Если он сидит не на крайнем стуле, то: перемещается налево при выпадении одного или двух очков; перемещается направо при выпадении трех или четырех очков; остается на том же месте при выпадении пяти или шести очков. Найти: а) матрицу вероятностей переходов за один шаг; б) вероятности следующих последовательностей: С,Д,Е,С,Д,А,С; С,В,Д,Е,Е,А; С,В,А,А,С,Д; С,Д,Е,С,Е,С; А,А,С,Д,Е,Е. 6 Студент, для получения профессионального образования, обучается в колледже в течение трех лет. Ежегодно он сдает комплексный экзамен. Если студент успешно сдаст экзамен, то он переводится на следующий курс или заканчивает колледж с дипломом специалиста. Если студент экзамен не сдает, то он остается на соответствующем курсе второй год. Вероятность успешной сдачи экзамена на первом году обучения составляет 0,7; втором – 0,8; третьем – 0,9. Указать подходящее число состояний системы. Найти матрицу вероятностей перехода за один шаг для ежегодных передвижений студента по курсам (первый, второй, третий год обучения, окончание колледжа). Определить вероятность, что студент будет обучаться на третьем курсе после сдачи второго экзамена. Определить среднее число лет, которые студент проводит в колледже.
ВАРИАЦИОННЫЕ РЯДЫ Ряд значений (вариант) признака, расположенных в порядке возрастания или убывания с соответствующими им весами (частотами или частостями), называется вариационными рядом (рядом распределения). Частота (ni) показывает, сколько раз встречается тот или иной вариант (значение признака) в статистической совокупности. Частость или относительная частота (wi) показывает, какая часть единиц совокупности принимает определенное значение или из интервала значений. В дискретных рядах перечисляются возможные значения признака
Дискретный ряд распределения можно изобразить графически в виде полигона распределения частот или частостей. В этом случае по оси абсцисс откладывают значения признака, а по оси ординат
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.240.72 (0.017 с.) |

 405с.
405с.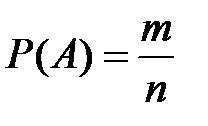 , (1.1)
, (1.1)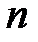 - общее число элементарных исходов (событий) в опыте или испытании;
- общее число элементарных исходов (событий) в опыте или испытании;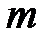 - число элементарных исходов (событий), благоприятствующих появлению события А.
- число элементарных исходов (событий), благоприятствующих появлению события А. (1.2)
(1.2)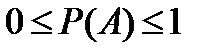 . (1.3)
. (1.3)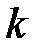 элементов из
элементов из  ; (1.4)
; (1.4)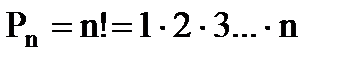 ; (1.5)
; (1.5)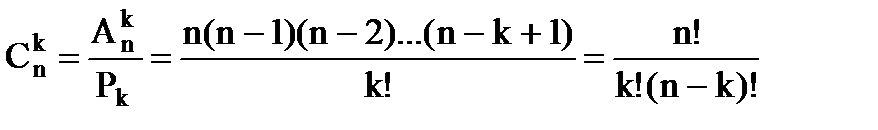 . (1.6)
. (1.6)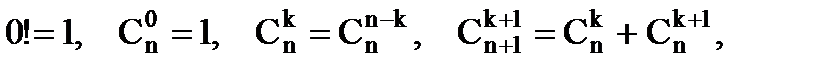
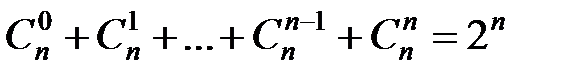 .
. ; α1 + α2 + … + αm = n;
; α1 + α2 + … + αm = n; 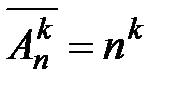 ;
; 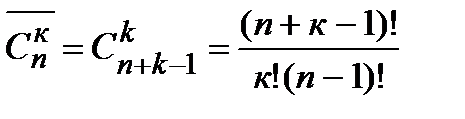 . (1.7)
. (1.7)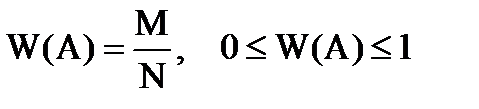 . (1.8)
. (1.8)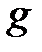 , брошенной в область
, брошенной в область 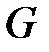 равна отношению меры (
равна отношению меры (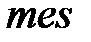 )области
)области 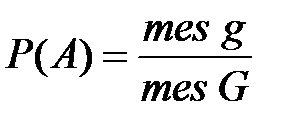 . (1.9)
. (1.9) .
.
 с той же вероятностью
с той же вероятностью 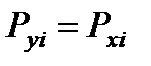 .
. . (7.1)
. (7.1) . (7/2)
. (7/2) и
и  то
то . (7.3)
. (7.3) . (7/4)
. (7/4) и их вероятности
и их вероятности  .
.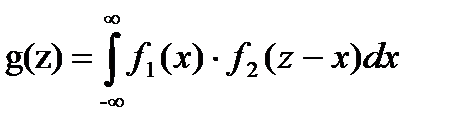 , или
, или  , (7.5)
, (7.5) , или
, или  . (7.6)
. (7.6)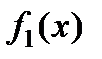 и
и  , то вероятность попадания случайной точки (Х, У) в область S равна:
, то вероятность попадания случайной точки (Х, У) в область S равна: . (7.7)
. (7.7) . Определить М(У).
. Определить М(У). . Определить М(У).
. Определить М(У).


 . Определить М(У), Д(У), σ(У).
. Определить М(У), Д(У), σ(У).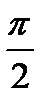 ;
;  ). Найти дифференциальную функцию случайной величины:
). Найти дифференциальную функцию случайной величины: =1. Найти дифференциальную функцию случайной величины:
=1. Найти дифференциальную функцию случайной величины: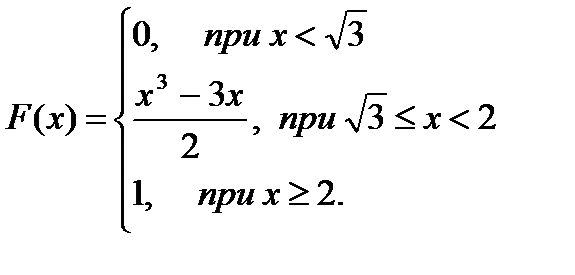
 ; б)
; б)  .
. .
.
 ,
,  .
. и средним квадратическим отклонением
и средним квадратическим отклонением 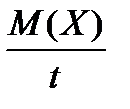 .
. . (8.1)
. (8.1) .
. . (8.2)
. (8.2) , то
, то . (8.3)
. (8.3)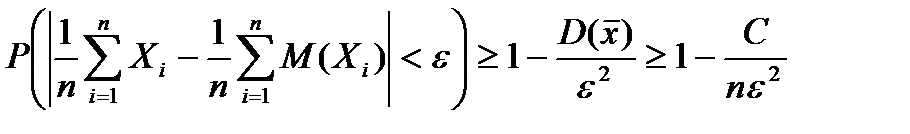 . (8.4)
. (8.4)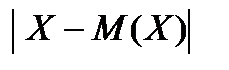 >3.
>3.
 . б) Определить вероятность того, что
. б) Определить вероятность того, что 
 . б) Определить вероятность того, что
. б) Определить вероятность того, что 
 , есть условная вероятность перехода случайного процесса из состояния Si в состояние
, есть условная вероятность перехода случайного процесса из состояния Si в состояние  за один шаг. Так как она не зависит от номера испытания, то может обозначаться через
за один шаг. Так как она не зависит от номера испытания, то может обозначаться через  . Первый индекс указывает номер предшествующего, а второй – последующего состояния. Если известны вероятности для любой пары состояния, то они могут быть представлены квадратной матрицей перехода.
. Первый индекс указывает номер предшествующего, а второй – последующего состояния. Если известны вероятности для любой пары состояния, то они могут быть представлены квадратной матрицей перехода. , где
, где 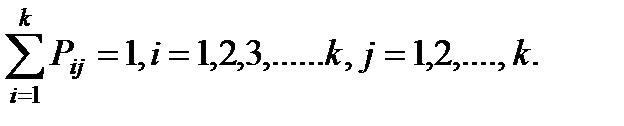 (10.1)
(10.1) в состояние S
в состояние S  за n шагов обозначается
за n шагов обозначается  , а квадратная матрица всех этих вероятностей обозначается
, а квадратная матрица всех этих вероятностей обозначается  . Вероятность перехода процесса из состояния i в состояние j за два шага вычисляется по формуле полной вероятности.
. Вероятность перехода процесса из состояния i в состояние j за два шага вычисляется по формуле полной вероятности.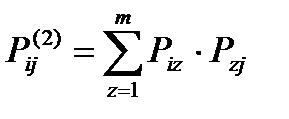 или в матричной записи
или в матричной записи 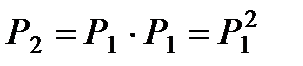 . (10.2)
. (10.2)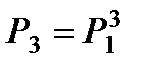 и за n – шагов
и за n – шагов  . (10.3)
. (10.3) б)
б)  .
.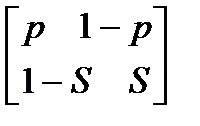
 вероятность того, что в момент времени t игральная кость лежит на грани «5», если в момент времени t=0, она находится в этом же положении?
вероятность того, что в момент времени t игральная кость лежит на грани «5», если в момент времени t=0, она находится в этом же положении? . Если признак непрерывный или число значений дискретного признака велико, то строят интервальный ряд распределения, в котором значения признака задаются в виде интервалов. При построении интервального ряда распределения число интервалов можно определить по формуле Стэрджесса: k=1+3,322 lg n, где n – число единиц совокупности. Величина интервала (h) определяется по формуле
. Если признак непрерывный или число значений дискретного признака велико, то строят интервальный ряд распределения, в котором значения признака задаются в виде интервалов. При построении интервального ряда распределения число интервалов можно определить по формуле Стэрджесса: k=1+3,322 lg n, где n – число единиц совокупности. Величина интервала (h) определяется по формуле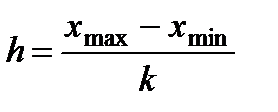 (8.1)
(8.1)


