
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра «Финансы и менеджмент»Содержание книги
Поиск на нашем сайте
Пример решения задачи прогнозирования сезонных показателей в среде Microsoft Excel Дана динамика некого условного показателя за 3 года по кварталам:
Предварительный графический анализ дает возможность сделать вывод о наличии динамики:
Определим, есть ли рост среднего показателя по годам:
Средние уровни по годам не демонстрируют устойчивой динамики:
Следовательно можно использовать индексы сезонности, для чего рассчитываем средние уровни показателя за каждый квартал и среднегодовой уровень показателя:
Сопоставим средние уровни по кварталам со среднегодовым уровнем показателя, зафиксировав знаменатель для использования функции АВТОЗАПОЛНЕНИЕ:
Перейдем к индексам сезонности:
Индексы сезонности демонстрируют наличие значимой сезонной волны: отклонения показателя от среднегодового уровня достигают 30%. Прогноз на следующий год тогда можно рассчитать через коэффициенты сезонности:
Получим прогнозные объемы по кварталам:
Задача 3. Провести анализ тренда валового внутреннего продукта за 28 месяцев.
Динамика ВВП, % к декабрю предыдущего года.
Спрогнозируйте ежемесячную динамику ВВП на год вперед.
Пример решения задачи среднесрочного прогнозирования на основе двухпараметрических кривых в среде Microsoft Excel
Снова рассмотрим некоторый условный показатель:
Выберем по внешнему виду графика аппроксимирующую кривую, для чего используем сглаженный ряд (см. выше):
Линейная функция:
Логарифмическая функция:
Парабола:
Степенная функция:
Экспонента:
По графикам видно, что линейная функция, полином второго порядка и экспонента одинаково близки с сглаженному ряду, поэтому выбираем линейную функцию:
Прогноз на следующие 2 периода можно рассчитать, используя уравнение на диаграмме:
Задача 1. Осуществить аппроксимацию по данным временного ряда индекса стоимости жизни:
Задача 2. Осуществить аппроксимацию по данным временного ряда спроса на условный товар в магазине:
Задача 3. Осуществить аппроксимацию по данным временного ряда объема продаж меховых шуб из песца в магазине "Меха": Занятие 6. Методы экстраполяции. Адаптивные методы прогнозирования. Метод экспоненциально-взвешенного среднего. Все адаптивные методы основаны на идее экспоненциально-взвешенного среднего (ЭВС):
где a - параметр сглаживания;
или
где
Пример решения задачи краткосрочного прогнозирования в среде Microsoft Excel Дана динамика некоторого условного показателя
Из графика видно, что ряд стационарный:
Cледовательно в качестве исходного прогноза на основе экспертной оценки можно использовать средний уровень ряда:
Получим 384,5556. Для стационарного ряда параметр сглаживания рекомендуется в размере 0,3.
В качестве экспертной оценки берем средний уровень ряда (384,5556), параметр сглаживания выбран 0,3. Тогда первый элемент рассчитывается следующим образом:
Задаем второй элемент ряда:
Остальные элементы получаем, используя функцию Автозаполнение:
Прогноз на момент времени t+1
Следовательно ряд прогноза имеет вид:
Оценим качество полученного прогноза.
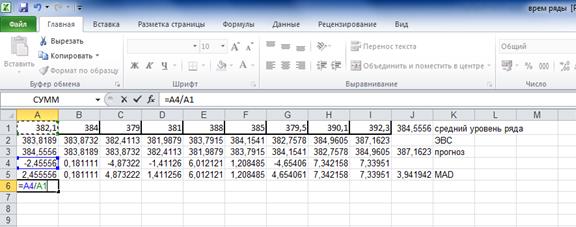
Рассчитаем среднее абсолютное отклонение:
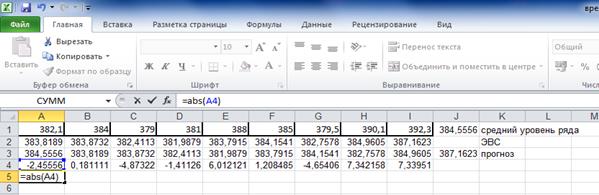
Для этого сначала рассчитаем отклонения фактических значений показателя от прогнозных:
Каждое отклонение возьмем по модулю:
Затем, используя функции Автозаполнение и Автосумма, найдем MAD:
Получим MAD=3,94 млн.р. Рассчитаем среднюю процентную ошибку:
и используя функции Автозаполнение и Автосумма, найдем MPE:
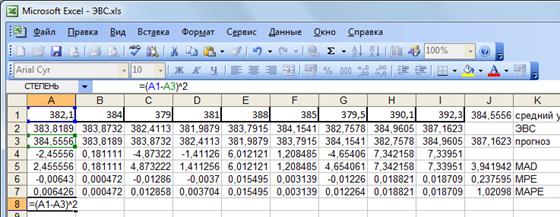
Получили MPE=0,237595% - средняя процентная ошибка близка к нулю, следовательно прогноз не смещен. Оценим точность прогноза, рассчитав среднюю абсолютную процентную ошибку:
Получили MAPE=1,02% - это значительно ниже 10%, что говорит об очень высокой точности прогноза. Определим верхнюю и нижнюю границы прогноза, для чего сначала рассчитаем среднее квадратическое отклонение. Величина среднеквадратического отклонения рассчитывается по формуле:
Границы прогноза принимаются как
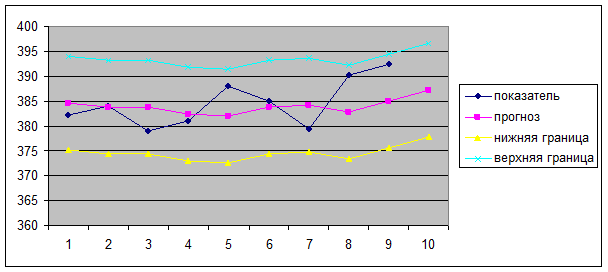
Итоговый график имеет вид:
Таким образом, прогноз на следующий период 387,1623 млн.р., верхняя граница прогноза 396,5632, нижняя граница 377,7615, прогноз не смещен (MPE= 0,237595% - значительно меньше 5%), точность прогноза можно оценить как очень высокую (MAPE= 1,02098% - значительно ниже 10%).
Метод Холта. Если среднее значение прогнозируемого показателя с течением времени меняется в соответствии с линейной функцией, то прогноз на t моментов времени вперед можно рассчитать по методу Холта:
где
Холт рекомендует следующие значения констант: А=0,1, В=0,01. Однако при рассмотрении конкретных экономических показателей значения констант могут корректироваться. В условиях сильного линейного роста метод Холта дает заниженные значения прогноза.
Библиографический список Основная литература 1. Минько Э.В. Методы прогнозирования и исследования операций [Электронный ресурс]: учебное пособие/ Минько Э.В., Минько А.Э.— Электрон. текстовые данные.— М.: Финансы и статистика, 2012.— 480 c.— Режим доступа: http://www.iprbookshop.ru/18821.— ЭБС «IPRbooks», по паролю 2. Молокова Е.И. Планирование деятельности предприятия [Электронный ресурс]: учебное пособие/ Молокова Е.И., Коваленко Н.П.— Электрон. текстовые данные.— Саратов: Вузовское образование, 2013.— 196 c.— Режим доступа: http://www.iprbookshop.ru/11394.— ЭБС «IPRbooks», по паролю 3. Савкина Р.В. Планирование на предприятии [Электронный ресурс]: учебник для бакалавров/ Савкина Р.В.— Электрон. текстовые данные.— М.: Дашков и К, 2014.— 320 c.— Режим доступа: http://www.iprbookshop.ru/24805.— ЭБС «IPRbooks», по паролю
Дополнительная литература 1. Мхитарян, В. C. Теория вероятностей и математическая статистика: учебник для вузов / В. C. Мхитарян, В. Ф. Шишов, А. Ю. Козлов.— Москва: Академия, 2012.— 413 с.: ил. — (Высшее профессиональное образование. Естественные науки) (Бакалавриат).—Библиогр. в конце кн. — ISBN 978-5-7695-8147-2 (в пер.).
Периодические издания 1. Экономическая наука современной России. 2. Экономист.
Интернет-ресурсы 1. http://www.iprbookshop.ru 2. http://library.tsu.tula.ru/ellibraries/all_news.htm) 3. www.gks.ru / Федеральная служба государственной статистики/ 4. www.minfin.ru / Министерство финансов РФ 5. www.minpromtorg.gov.ru / Министерство промышленности и торговли РФ/ 6. www.rbc.ru / РосБизнесКонсалтинг/
Кафедра «Финансы и менеджмент»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям
по дисциплине " Планирование и прогнозирование в условиях рынках"
Направление подготовки: 38.03.01 «Экономика»
Специальности подготовки: «Финансы и кредит», «Бухгалтерский учет, анализ и аудит», «Налоги и налогообложение»
Форма обучения: очная, заочная
Тула 2015 г.
Методические указания составлены доц. Н.Н. Макаровой и обсуждены на заседании кафедры «Финансы и менеджмент» Протокол № 11 от 30 марта 2015 г.
Зав. кафедрой _______________Е.А. Федорова
1 Цель и задачи освоения учебной дисциплины
Цель дисциплины – формирование знаний и навыков по методам прогнозирования тенденций экономического и социального развития страны, рынка, предприятия, по моделированию и планированию темпов, пропорций развития народного хозяйства, по планированию деятельности предприятий в современных условиях. Задачи дисциплины: - показать принципы научного подхода к прогнозированию экономических процессов и явлений на макро- и микроуровне; - вскрыть взаимосвязи и взаимопроникающий характер прогнозирования и планирования экономических явлений в условиях рынка; -освоить методологические основы и принципы прогнозирования и планирования развития народного хозяйства на макро- и микроуровне.
Занятие 1. Понятие временного ряда в экономическом прогнозировании.
Непосредственно до этапа прогнозирования экономических показателей объект прогнозирования необходимо проанализировать. Для характеристики интенсивности изменения во времени используются показатели: 1) абсолютный прирост, Расчет показателей динамики представлен в следующей таблице.
* В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях. Рассмотрим пример. Имеются данные об объемах и динамике продаж акций на 15 крупнейших биржах России за пять месяцев.
В процессе анализа могут быть рассчитаны следующие средние показатели динамики: · средний уровень ряда, или средняя хронологическая; · средний абсолютный прирост; · средний темп роста; · средний темп прироста. Средний уровень ряда показывает, какая средняя величина уровня характерна для всего анализируемого периода. К его расчету прибегают для рядов, состояние или изменение которых стабильно в течение большого периода времени, и рядов с уровнями, колеблющимися в короткие промежутки времени. Показатель рассчитывается различно для интервальных и моментных рядов. Для интервального ряда сумма значений фактических показателей временного ряда делится на число показателей:
Для моментного ряда расчет осуществляется по формуле (1.2). Следует учесть, что значения первого и последнего показателей временного ряда берутся в половинном размере, поэтому в знаменателе количество показателей уменьшается на единицу.
Средний абсолютный прирост ряда показывает скорость развития явления и рассчитывается по формуле
где
п — число показателей временного ряда. Средний темп роста может быть рассчитан по формуле средней геометрической, при сравнении последнего показателя временного ряда с первым расчет осуществляется по формуле
Средний темп прироста определяется по формуле
Следует учесть, что средние показатели можно использовать только для равномерно меняющихся явлений.
Рассмотрим пример. Товарооборот предприятия характеризуется следующими показателями (млн. руб.):
Предварительное изучение ряда демонстрирует наличие устойчивой динамики роста:
Следовательно для прогнозирования можно использовать средние показатели динамики (исключая средний уровень ряда).
Рассчитаем средний абсолютный прирост:
Тогда прогноз на следующий период можно определить как последний уровень ряда плюс средний прирост:
Рассчитаем теперь средний коэффициент роста:
Рассчитаем прогнозный уровень ряда:
Аналогично можно осуществить прогнозирование через другие средние показатели: Темп роста:
Коэффициент прироста.
Темп прироста.
Задача 1. По данным временного ряда спрогнозировать значение на 3 периода вперед.
Задача 2. По данным временного ряда спрогнозировать значение на 2 момента времени вперед.
Часто при анализе динамических рядов можно столкнуться с таким явлением как сезонность.
Пример решения задачи прогнозирования сезонных показателей в среде Microsoft Excel Дана динамика некого условного показателя за 3 года по кварталам:
Предварительный графический анализ дает возможность сделать вывод о наличии динамики:
Определим, есть ли рост среднего показателя по годам:
Средние уровни по годам не демонстрируют устойчивой динамики:
Следовательно можно использовать индексы сезонности, для чего рассчитываем средние уровни показателя за каждый квартал и среднегодовой уровень показателя:
Сопоставим средние уровни по кварталам со среднегодовым уровнем показателя, зафиксировав знаменатель для использования функции АВТОЗАПОЛНЕНИЕ:
Перейдем к индексам сезонности:
Индексы сезонности демонстрируют наличие значимой сезонной волны: отклонения показателя от среднегодового уровня достигают 30%. Прогноз на следующий год тогда можно рассчитать через коэффициенты сезонности:
Получим прогнозные объемы по кварталам:
Задача 3. Провести анализ тренда валового внутреннего продукта за 28 месяцев.
Динамика ВВП, % к декабрю предыдущего года.
Спрогнозируйте ежемесячную динамику ВВП на год вперед.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.82.108 (0.01 с.) |

















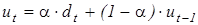 , (6.1)
, (6.1)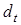 - фактическое значение показателя, соответствующее текущему моменту времени t;
- фактическое значение показателя, соответствующее текущему моменту времени t;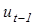 - предыдущее значение ЭВС в момент времени t-1. В момент времени t=1 предыдущее значение ЭВС определяют на основе экспертной оценки.
- предыдущее значение ЭВС в момент времени t-1. В момент времени t=1 предыдущее значение ЭВС определяют на основе экспертной оценки.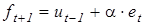 , (6.2)
, (6.2)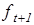 - прогноз на следующий момент времени,
- прогноз на следующий момент времени, - текущее значение ошибки прогноза.
- текущее значение ошибки прогноза.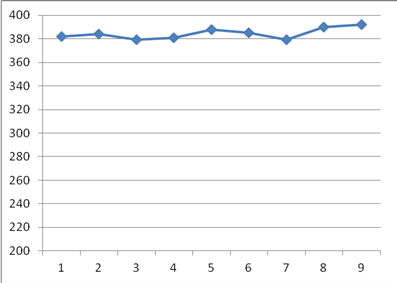
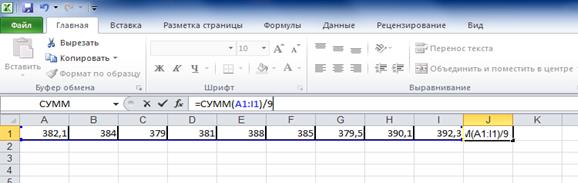
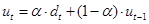 Рассчитаем ЭВС:
Рассчитаем ЭВС:

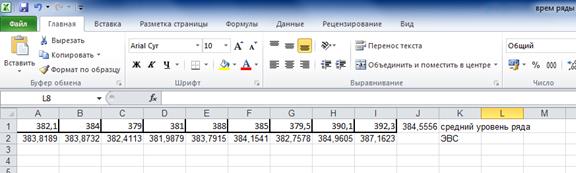
 принимается равным текущему значению ЭВС:
принимается равным текущему значению ЭВС: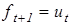

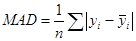 , где
, где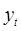 — фактическое значение в момент времени t,
— фактическое значение в момент времени t,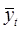 — прогнозное значение в момент времени t.
— прогнозное значение в момент времени t.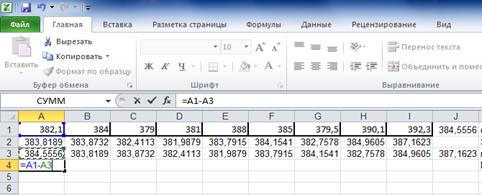

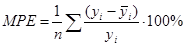

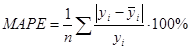


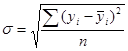

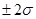 :
:
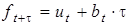 , (6.7)
, (6.7) - оценка стационарного фактора:
- оценка стационарного фактора: , (6.8)
, (6.8) - оценка линейного роста:
- оценка линейного роста: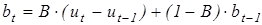 , (6.9)
, (6.9) - предыдущее значение оценки линейного роста (в момент времени t=1 предыдущее значение оценки линейного роста принимается равным нулю),
- предыдущее значение оценки линейного роста (в момент времени t=1 предыдущее значение оценки линейного роста принимается равным нулю), *
*





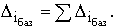

 (1.1)
(1.1) (1.2)
(1.2) , (1.3)
, (1.3) — первый зарегистрированный показатель временного ряда;
— первый зарегистрированный показатель временного ряда; — последний зарегистрированный показатель временного ряда;
— последний зарегистрированный показатель временного ряда; *100%. (1.4)
*100%. (1.4) (1.5)
(1.5)



















