Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие 5. Оценка качества количественных прогнозов.Содержание книги
Поиск на нашем сайте
На практике, получая прогнозный результат в виде точечного значения
где
Для определения границ доверительного интервала используется выражение
где Величина среднеквадратического отклонения рассчитывается по формуле
где
п — число наблюдений (размер выборки). Среднеквадратическое отклонение характеризует, насколько точно теоретическая кривая описывает поведение исследуемой характеристики в прошлом. Величина
После наступления прогнозируемого события ошибка прогноза определяется как разность между фактическим и прогнозным значением показателя.
Для обобщенной оценки метода прогнозирования на практике могут быть использованы следующие способы оценки средней ошибки прогноза (погрешности): · среднее абсолютное отклонение (mean absolute derivation, MAD). Использование этого показателя имеет смысл, когда исследователю необходимо оценить ошибку в тех же единицах, что и исходный ряд:
· средняя процентная ошибка (mean percentage error, МРЕ) позволяет оценить возможное смещение прогноза, когда полученный прогноз окажется завышенным или заниженным. При несмещенном прогнозе имеем величину ошибки, близкую к нулю, при завышенном — большое положительное процентное значение, при заниженном — большое отрицательное. При условии, что потери при прогнозировании, связанные с завышением фактического будущего значения, уравновешиваются занижением, идеальный прогноз должен быть несмещенным, и значение средней процентной ошибки должно стремиться к нулю. На практике допустимым считается значение средней процентной ошибки, не превышающее 5%:
· средняя абсолютная ошибка в процентах (mean absolute percentage error, MAPE):
Для оценки точности прогнозов используют следующую шкалу:
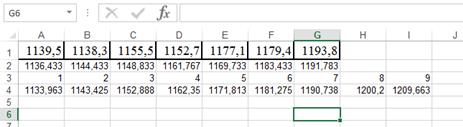
Приведенные выше способы оценки качества прогноза позволяют осуществить сравнение результатов, полученных различными методами прогнозирования, и выбрать наиболее приемлемый метод для решения прогнозной задачи. Вернемся к примеру с условным показателем (см. выше):
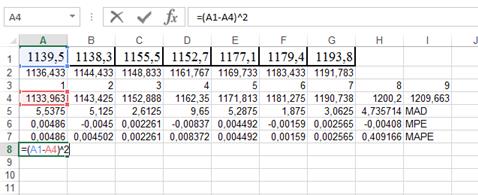
Рассчитаем MAD:
Применяем функцию АВТОЗАПОЛНЕНИЕ:
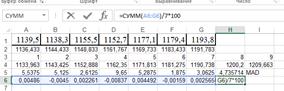
И применяем формулу:
Далее определим МРЕ:
Применив функции АВТОЗАПОЛНЕНИЕ и СУММ:
получим:
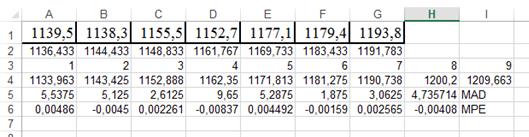
Процентная ошибка значимо не отличается от нуля (-0,00408), т.е. прогноз не смещен.
Определим МАРЕ:
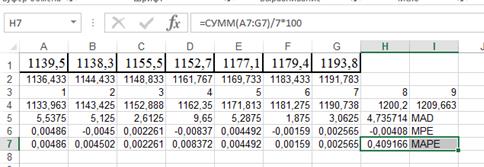
Аналогично предыдущему расчету применив функции АВТОЗАПОЛНЕНИЕ и СУММ, получим:
Так как МАРЕ значительно меньше 10%, точность очень высокая.
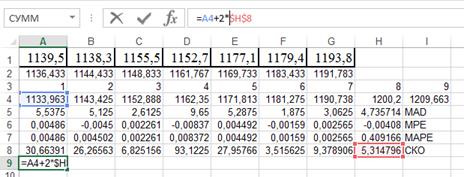
Теперь необходимо оценить ошибку прогнозирования на будущие периоды, для этого рассчитаем СКО:
Через СКО рассчитаем границы прогноза, приняв значение критерия Стьюдента равным 2:
Таким образом, прогноз на 8 год 1200,2 (от 1189,57 до 1210,83), на 9 год 1209,663 (от 1199,033 до 1220,292).
Задача 1. Оценить качество прогноза из задачи 1 предыдущего занятия.
Задача 2. Оценить качество прогноза из задачи 2 предыдущего занятия.
Задача 3. Оценить качество прогноза из задачи 3 предыдущего занятия.
Занятие 6. Методы экстраполяции.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 804; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.198.181 (0.006 с.) |

 , необходимо указать и возможную величину ошибки
, необходимо указать и возможную величину ошибки  , т.е. перейти к интервальному прогнозу по формуле
, т.е. перейти к интервальному прогнозу по формуле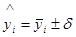 , (5.1)
, (5.1) — интервальное значение прогнозной характеристики;
— интервальное значение прогнозной характеристики;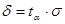 , (5.2)
, (5.2) — среднеквадратическое отклонение;
— среднеквадратическое отклонение; 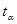 — критерий Стьюдента.
— критерий Стьюдента. , (5.3)
, (5.3) — фактическое значение исследуемой характеристики на участке ретроспекции;
— фактическое значение исследуемой характеристики на участке ретроспекции; , (5.4)
, (5.4) ; (5.5)
; (5.5)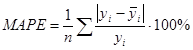 . (5.6)
. (5.6) , %
, %