
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Адаптивные методы прогнозирования.Содержание книги
Поиск на нашем сайте
Метод экспоненциально-взвешенного среднего. Все адаптивные методы основаны на идее экспоненциально-взвешенного среднего (ЭВС):
где a - параметр сглаживания;
или
где
Пример решения задачи краткосрочного прогнозирования в среде Microsoft Excel Дана динамика некоторого условного показателя
Из графика видно, что ряд стационарный:
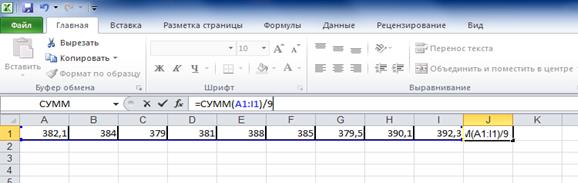
Cледовательно в качестве исходного прогноза на основе экспертной оценки можно использовать средний уровень ряда:
Получим 384,5556. Для стационарного ряда параметр сглаживания рекомендуется в размере 0,3.
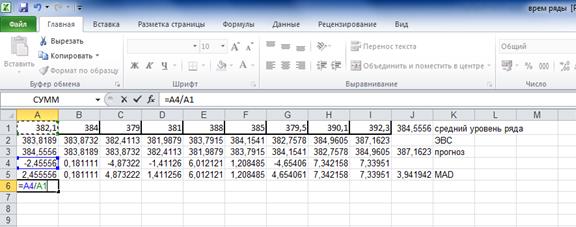
В качестве экспертной оценки берем средний уровень ряда (384,5556), параметр сглаживания выбран 0,3. Тогда первый элемент рассчитывается следующим образом:
Задаем второй элемент ряда:
Остальные элементы получаем, используя функцию Автозаполнение:
Прогноз на момент времени t+1
Следовательно ряд прогноза имеет вид:
Оценим качество полученного прогноза.
Рассчитаем среднее абсолютное отклонение:
Для этого сначала рассчитаем отклонения фактических значений показателя от прогнозных:
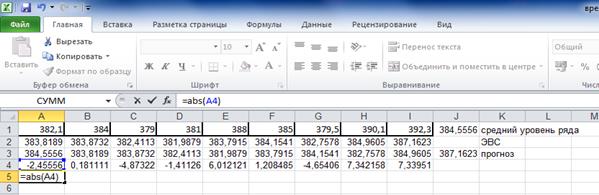
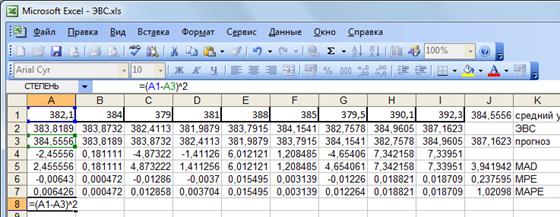
Каждое отклонение возьмем по модулю:
Затем, используя функции Автозаполнение и Автосумма, найдем MAD:
Получим MAD=3,94 млн.р. Рассчитаем среднюю процентную ошибку:
и используя функции Автозаполнение и Автосумма, найдем MPE:
Получили MPE=0,237595% - средняя процентная ошибка близка к нулю, следовательно прогноз не смещен. Оценим точность прогноза, рассчитав среднюю абсолютную процентную ошибку:
Получили MAPE=1,02% - это значительно ниже 10%, что говорит об очень высокой точности прогноза. Определим верхнюю и нижнюю границы прогноза, для чего сначала рассчитаем среднее квадратическое отклонение. Величина среднеквадратического отклонения рассчитывается по формуле:
Границы прогноза принимаются как
Итоговый график имеет вид:
Таким образом, прогноз на следующий период 387,1623 млн.р., верхняя граница прогноза 396,5632, нижняя граница 377,7615, прогноз не смещен (MPE= 0,237595% - значительно меньше 5%), точность прогноза можно оценить как очень высокую (MAPE= 1,02098% - значительно ниже 10%).
Метод адаптивной скорости реакции. Если в изменении показателя предполагаются переходы среднего значения на новый уровень и дальнейшие колебания относительно нового уровня, то для прогнозирования показателя можно использовать метод адаптивной скорости реакции. Этот метод основан на адаптации к поступающим данным. В качестве параметра сглаживания здесь используется не постоянная величина a, а рассчитываемое для каждого момента времени значение трекинг-сигнала:
где
Прогноз на следующий момент времени по модели адаптивной скорости реакции рассчитывается следующим образом:
где Метод Холта. Если среднее значение прогнозируемого показателя с течением времени меняется в соответствии с линейной функцией, то прогноз на t моментов времени вперед можно рассчитать по методу Холта:
где
Холт рекомендует следующие значения констант: А=0,1, В=0,01. Однако при рассмотрении конкретных экономических показателей значения констант могут корректироваться. В условиях сильного линейного роста метод Холта дает заниженные значения прогноза.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 785; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.244.34 (0.006 с.) |

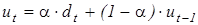 , (6.1)
, (6.1)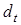 - фактическое значение показателя, соответствующее текущему моменту времени t;
- фактическое значение показателя, соответствующее текущему моменту времени t;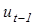 - предыдущее значение ЭВС в момент времени t-1. В момент времени t=1 предыдущее значение ЭВС определяют на основе экспертной оценки.
- предыдущее значение ЭВС в момент времени t-1. В момент времени t=1 предыдущее значение ЭВС определяют на основе экспертной оценки.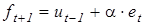 , (6.2)
, (6.2)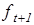 - прогноз на следующий момент времени,
- прогноз на следующий момент времени, - текущее значение ошибки прогноза.
- текущее значение ошибки прогноза.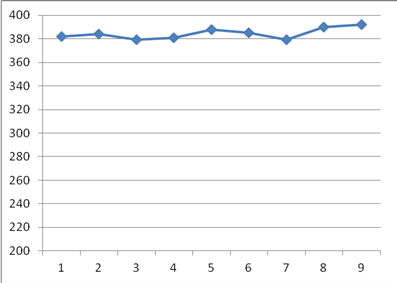
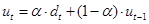 Рассчитаем ЭВС:
Рассчитаем ЭВС:

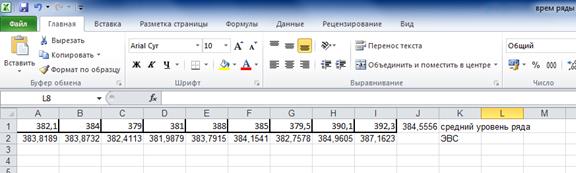
 принимается равным текущему значению ЭВС:
принимается равным текущему значению ЭВС: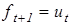

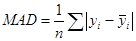 , где
, где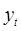 — фактическое значение в момент времени t,
— фактическое значение в момент времени t,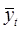 — прогнозное значение в момент времени t.
— прогнозное значение в момент времени t.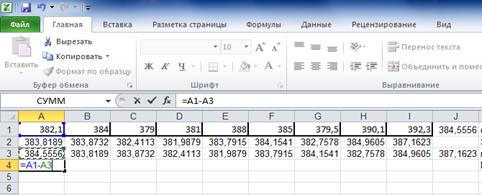

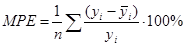

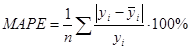


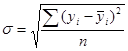

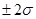 :
:
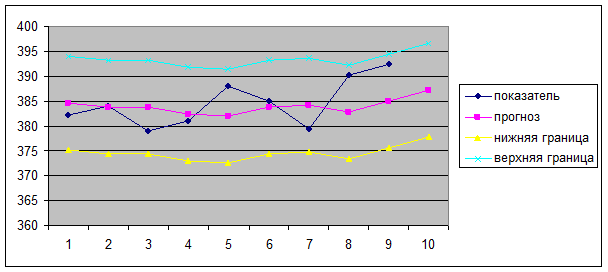
 , (6.3)
, (6.3)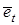 - экспоненциально взвешенная ошибка:
- экспоненциально взвешенная ошибка: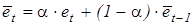 , (6.4)
, (6.4)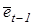 - предыдущее значение экспоненциально взвешенной ошибки (в момент времени t=1 предыдущее значение экспоненциально взвешенной ошибки принимается равным нулю),
- предыдущее значение экспоненциально взвешенной ошибки (в момент времени t=1 предыдущее значение экспоненциально взвешенной ошибки принимается равным нулю),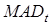 - среднее абсолютное отклонение ошибки (Mean Absolute Deviation):
- среднее абсолютное отклонение ошибки (Mean Absolute Deviation): , (6.5)
, (6.5)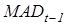 - предыдущее значение среднего абсолютного отклонения ошибки (в момент времени t=1 предыдущее значение среднего абсолютного отклонения принимается равным 0,1
- предыдущее значение среднего абсолютного отклонения ошибки (в момент времени t=1 предыдущее значение среднего абсолютного отклонения принимается равным 0,1 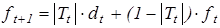 , (6.6)
, (6.6)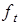 - значение текущего прогноза показателя (в момент времени t=1 текущее значение прогноза определяется на основе экспертной оценки).
- значение текущего прогноза показателя (в момент времени t=1 текущее значение прогноза определяется на основе экспертной оценки).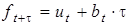 , (6.7)
, (6.7) - оценка стационарного фактора:
- оценка стационарного фактора: , (6.8)
, (6.8) - оценка линейного роста:
- оценка линейного роста: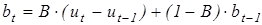 , (6.9)
, (6.9) - предыдущее значение оценки линейного роста (в момент времени t=1 предыдущее значение оценки линейного роста принимается равным нулю),
- предыдущее значение оценки линейного роста (в момент времени t=1 предыдущее значение оценки линейного роста принимается равным нулю),


