
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сезонно-декомпозиционная модель Холта-Винтера.Содержание книги
Поиск на нашем сайте
Используется для описания комбинации линейного и сезонно-аддитивного тренда. Модель предполагает, что характеристики временного ряда – стационарность, линейность и сезонность – могут быть разделены, изучены и оценены изолированно. Окончательный прогноз осуществляется сведением прогнозов различных элементов в один. а) Оценка стационарного фактора:
б) Оценка линейного роста:
в) Оценка сезонного фактора:
где
Коэффициент сезонности представляет собой отношение значения текущего наблюдения к среднестационарному значению показателя. Коэффициент сезонности можно найти по формуле
при этом для расчета стационарного фактора Рекомендуемые значения констант для формул (6.10) – (6.12): А=0,2; В=0,2; С=0,5. Прогноз на t моментов времени вперед, составляющие которого определены по формулам (6.10) – (6.12), рассчитывается по формуле
При использовании модели Холта-Винтера рекомендуется следующий алгоритм расчета. По данным динамики показателя за предыдущий год рассчитывают оценки коэффициентов сезонности Ft. В качестве момента времени t=1 принимают значение показателя в январе или I квартале года, предшествующего текущему. Затем по формулам (6.10) – (6.12) находят оценки стационарного фактора, линейного роста и коэффициентов сезонности для текущего года. Прогноз осуществляется на базе найденных составляющих элементов по формуле (6.13), где обозначение коэффициента сезонности
Задача 1. По квартальным данным временного ряда объема импорта из некой условной страны спрогнозировать значения импорта на следующий квартал. Оценить верхнюю и нижнюю границу прогноза. Оценить: точность прогноза на основе средней абсолютной процентной ошибки; смещенность прогноза на основе средней процентной ошибки. Построить графики временного ряда показателя, прогнозного значения, верхней и нижней границ прогноза.
Объем импорта за 3 года, млн. у.е. Указание: используйте экспоненциально взвешенное среднее. Задача 2. Выполните задачу 1, используя метод адаптивной скорости реакции на основе трекинг-сигнала. Сравните результаты первого и второго методов.
Задача 3. По ежемесячным данным временного ряда спроса на видеомагнитофоны спрогнозировать значение спроса на 3 месяца вперед. Оценить верхнюю и нижнюю границу прогноза. Оценить: точность прогноза на основе средней абсолютной процентной ошибки; смещенность прогноза на основе средней процентной ошибки. Построить графики временного ряда показателя, прогнозного значения, верхней и нижней границ прогноза.
Объем спроса на видеомагнитофоны за год, шт. Указание: используйте метод Холта.
Задача 4. Выполните задачу 3, используя метод двойного сглаживания Брауна. Сравните результаты.
Задача 5. По еженедельным данным временного ряда спрогнозировать значение на 3 недели вперед. Оценить верхнюю и нижнюю границу прогноза. Оценить: точность прогноза на основе средней абсолютной процентной ошибки; смещенность прогноза на основе средней процентной ошибки. Построить графики временного ряда показателя, прогнозного значения, верхней и нижней границ прогноза.
Указание: используйте метод адаптивного сглаживания Брауна. Занятие 7. Нормативный метод планирования. Нормативный метод основан на определении и использовании в процессе планирования системы норм и нормативов. Норма – это научно обоснованная мера затрат ресурса на изготовление единицы продукции в конкретных производственно-технических условиях.
Нормативы отражают общественные требования к результатам деятельности и характеризуют необходимый уровень использования ресурса. Комплекс норм и нормативов, используемых для разработки плановых документов, называется нормативной базой. Сам по себе нормативный метод самый лёгкий и простой в применении из всех остальных методов планирования. Так, например, если норма времени на изготовление изделия – 10 часов ( Основная сложность при применении нормативного метода заключается в определении величины нормы. Существуют следующие основные методы разработки норм и нормативов: 1. научного обоснования; 2. аналитически-расчетный; 3. аналитически-исследовательский; 4. опытный; 5. отчетно-статистический. Метод научного обоснования нормы позволяет находить оптимальное значение нормы с учетом действия технических, экономических, социальных и других факторов, оказывающих влияние на ее величину. Пример. Магазин закупает хлеб на хлебозаводе по цене 10 рублей за батон, а продает по 11 руб. Если хлеб не будет реализован в день завоза, то на следующий день его продают по 8 рублей за батон (с одой стороны это связано с ухудшением качества продукции, а с другой стороны, присутствует определённый элемент рекламы). Необходимо определить ежедневную норму завоза хлеба, обеспечивающую максимум прибыли. Данные об объемах реализации хлеба в течение прошлой недели представлены в табл. 7.1. Таблица 7.1 Объемы реализации хлеба в течение недели
Решение. Прежде всего, рассчитаем средний объем реализации хлеба за день:
Номинальная прибыль от реализации хлеба составляет: Обозначим вероятность продажи
С другой стороны, ожидаемый убыток связанный с не реализацией (а значит с ухудшением качества)
где Для определения оптимальной нормы завоза необходимо уравновесить ожидаемую прибыль и убыток:
Отсюда, вероятность реализации хлеба:
Значит, ежедневная норма завоза хлеба должна составлять такое количество буханок, вероятность продажи которых равна 0,67 или 67%. Будем считать, что исследуемое нами явление, как и большинство других экономических процессов подчиняется нормальному закону распределения. Тогда с ростом нормы завоза хлеба вероятность реализации всего завоза будет уменьшаться по зависимости изображенной на рис. 7.1.
0,67
норма, шт.
Рис. 7.1. Зависимость вероятности реализации заказа от его размера
Таким образом, величину нормы можно определить из выражения:
где
Соответственно, ежедневная норма завоза хлеба:
Существует достаточно большое количество разнообразных примеров применения метода научного обоснования нормы. При этом, с целью определения оптимальной (по определенному критерию) нормы могут использоваться экономико-статистические, оптимизационные и другие модели. Аналитически-расчётный метод основан на разделении выполняемых работ на составные элементы с последующим их анализом и проектированием рациональных вариантов использования материальных ресурсов, оборудования и рабочей силы. Пример. Из прутка стандартной длины - 3 метра нарезаются заготовки вида А - 80 см и вида Б - 52 см. Применяемость данных заготовок в изделии: А – 2 шт., Б – 2 шт. Масса 1 метра погонного прутка 2,4 кг. Ширина распила – 5мм. Определить норму расхода материала на изделие. Решение. Рассмотрим возможные варианты распила прутка. Первоначально попытаемся нарезать как можно больше заготовок вида А (так как они самые длинные), а из оставшегося материала заготовки меньшей длины – Б. В последующих вариантах будем уменьшать количество нарезаемых заготовок вида А на одну единицу. Вариант 1. 3 А и 1 Б, Отходы материала:
Вариант 2. 2 А и 2 Б, Отходы материала:
Вариант 3. 1 А и 4 Б, Отходы материала:
Вариант 4. 0 А и 5 Б, Отходы материала:
На первый взгляд самым подходящим является вариант №2. Из одного прутка данным способом можно вырезать 2 заготовки вида А и 2 вида Б, т.е., комплект заготовок на одно изделие. Следовательно, норма затрат материала – 3 метра погонных на изделие, или а) Рассмотрим сочетание 1 и 3-го вариантов. Обозначим
Значит, при сочетании 1 и 3 вариантов из 5 прутков - 3 следует разрезать 1-м способом, а 2 прутка 3-м способом. В этом случае мы получаем:
Норма: б) Рассмотрим сочетание 1 и 4-го вариантов. Обозначим
Это значит, что из 7 прутков 1-м вариантом разрезаем 5, а 2-м – 2 прутка. Количество заготовок: Норма: Анализ возможных вариантов распила прутков показывает, что наиболее целесообразным является сочетание 1 и 3 вариантов, так как в этом случае норма расхода материалов будет наименьшей ( Аналитически-исследовательский метод основан на определении норм путем проведения наблюдений и экспериментов. Данный метод нашел широкое применение на действующих производствах. С помощью наблюдений, как правило, определяются нормы затрат времени на выполнение технологических операций. Часто в ходе наблюдений и экспериментов изучается возможность и оценивается целесообразность внедрения различных вспомогательных приспособлений, снижающих затраты времени на выполнение операций. Таким образом, практическое применение аналитическо-исследовательского метода направлено не только на определение значений нормируемых параметров, но и на совершенствование технологического процесса. Отчётно-статистический метод заключается в том, что нормы затрат производственных ресурсов устанавливаются на основе отчётных или статистических данных за прошедшие периоды. Пример. Имеются отчетные данные по энергопотреблению цехом, выпускающим продукцию двух наименований (табл. 7.2). Определить нормы затрат электроэнергии на изготовление продукции вида А и Б, а также, затраты на освещение цеха. Таблица 7.2 Затраты электроэнергии на выпуск продукции
Решение. Обозначим нормы затрат электроэнергии на изготовление продукции вида А, Б и затраты на освещение -
Из второго уравнения вычитаем первое и получаем: Для дальнейшего планирования энергопотребления можно использовать следующее выражение:
После подстановки в данное выражение планируемого выпуска продукции вида А ( Задача 1. Объемы реализации продукта в течение 7 месяцев.
Стоимость закупки 1 упаковки 200 р., продажная цена 300 р., срок хранения неделя. Определить норму завоза товара, обеспечивающую наибольшую прибыль.
Задача 2. Сталепрокатный завод производит стальные листы трех различных размеров: 100 дюймов, 80 дюймов и 55 дюймов. Поступил заказ на стальные листы размером 45, 30 и 18 дюймов в количестве 150, 200 и 185 штук соответственно. Каким образом компания должна разрезать стальные листы, чтобы минимизировать отходы? Учтите, что желательно также при раскрое не получать слишком много лишних листов с размерами, заданными данным заказчиком.
Задача 3. Затраты электроэнергии на выпуск продукции
Определить норматив затрат.
Занятие 8. Балансовый метод планирования.
Балансовый метод заключается в уравновешивании результатов производственной деятельности с одной стороны и затрачиваемых ресурсов с другой. Различают материальные, стоимостные и трудовые балансы. Центральное место в системе экономических балансов занимают материальные балансы. По виду используемой балансовой модели балансы бывают однопродуктовыми и межпродуктовыми. Однопродуктовые балансы разрабатываются по конкретному виду продукции. Многопродуктовые балансы увязывают производство продукции и потребление ресурсов между отраслями экономики. Разработка материальных балансов начинается с определения потребностей общества в продукции каждого вида. Для определения потребности общества в продукции того или иного вида чаще всего используется нормативный метод. Например, потребность в молокопродуктах определяется произведением рациональной нормы потребления молокопродуктов, приходящейся на одного человека, на численность населения. После определения потребностей в продукции формируется ресурсная часть баланса. Широкое распространение для анализа межотраслевых связей и формирования структуры национальной экономики получили межотраслевые балансы в стоимостном и материальном выражении. Информационная модель межотраслевого баланса в стоимостном выражении представлена в табл. 3. Межотраслевой баланс в стоимостном выражении состоит из четырёх квадрантов. В первом квадранте отражаются финансовые потоки между отраслями производителями и отраслями потребителями материальных ресурсов. Также в этом квадранте определяется промежуточное потребление и промежуточные затраты на производство продукции отраслями. Во втором квадранте характеризуется потребление конечного продукта, который включает конечное потребление продукции в домашних хозяйствах, валовое накопление, сальдо экспортно-импортных операций. В третьем квадранте приводятся данные об амортизационных отчислениях, заработной плате, прибыли и налогах по отраслям. В четвёртом квадранте отражается перераспределение национального дохода. Исходя из условия равенства валового выпуска и затрат получаем следующие уравнения:
или, например, для первой отрасли имеем:
Таблица Информационная модель межотраслевого баланса в стоимостном выражении
Рассмотрим решение задачи: Даны коэффициенты прямых затрат
Требуется определить: 1. коэффициенты полных затрат. 2. проверить продуктивность матрицы А. 3. вектор валового выпуска. 4. межотраслевые поставки продукции. 5. заполнить схему межотраслевого баланса.
Для решения задачи воспользуемся программным пакетом EXCEL.
1. В ячейки рабочего поля программы запишем элементы матрицы А, а рядом – единичную матрицу Е:
Массив Е-А можно получить, выделив ячейки, где желателен ответ, задав в строке fx:
и нажав CTRL+SHIFT+ENTER. Необязательно набирать это вручную, можно выделять соответствующие ячейки мышью.
Теперь выделяем диапазон, в котором будет получена обратная матрица
Для получения ответа по элементам необходимо нажать клавиши CTRL+SHIFT+ENTER:
2. Все элементы матрицы полных затрат неотрицательны, следовательно матрица А продуктивна. 3. Вектор валового выпуска вычисляется по формуле:
Для нахождения вектора валового выпуска вводим вектор Y и нажав fx выбираем формулу перемножения матриц:
Как и ранее, нажимаем CTRL+SHIFT+ENTER, чтобы получить ответ по элементам:
4. Межотраслевые поставки вычисляем по формуле:
Для этого опять используем формулу МУМНОЖ, перемножая по элементам:
Перемножив по очереди все три столбца матрицы А на соответствующие элементы вектора валового выпуска, получим матрицу межотраслевых поставок:
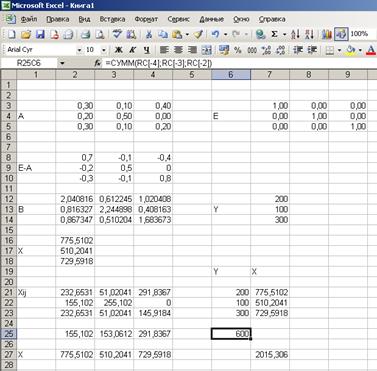
5. Теперь можно заполнить схему межотраслевого баланса:
Валовой продукт первой отрасли должен быть равен сумме произведенного первой отраслью для всех отраслей и конечного продукта:
Аналогично для второй и третьей отраслей. Условно чистая продукция отрасли – это разница между валовым продуктом отрасли и ее промежуточным потреблением:
Сумма условно-чистых продукций отраслей должна быть равна общему объему конечного продукта:
Задача 1. Каким должен быть валовой выпуск продукции промышленности, сельского хозяйства, строительства, если прогноз спроса на конечную продукцию составил по промышленности Y1= 15 млрд. долл., по сельскому хозяйству Y2= 3 млрд. долл., по строительству Y3=7 млрд. долл. Построить межотраслевой баланс. Матрица коэффициентов прямых затрат имеет вид: А=
Задача 2. Каковы должны быть цены на продукцию топливно-энергетической отрасли, промышленности и сельского хозяйства, чтобы экономика находилась в сбалансированном состоянии, при условии, что вектор норм добавленной стоимости имеет вид: А= Как должны измениться цены в этих отраслях, если норма добавленной стоимости в топливно-энергетической компании увеличится на 1,11.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 851; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.11.132 (0.012 с.) |

 , (6.10)
, (6.10) , (6.11)
, (6.11) , (6.12)
, (6.12) - коэффициент сезонности, соответствующий моменту времени t,
- коэффициент сезонности, соответствующий моменту времени t, - коэффициент сезонности, соответствующий моменту времени t-L, то есть сдвинутому на L моментов времени назад. L – длина сезонного цикла или количество временных отрезков в цикле (для месяцев L=12, для кварталов L=4).
- коэффициент сезонности, соответствующий моменту времени t-L, то есть сдвинутому на L моментов времени назад. L – длина сезонного цикла или количество временных отрезков в цикле (для месяцев L=12, для кварталов L=4). ,
, можно использовать формулу (6.1), если среднее значение показателя за год меняется незначительно, или по формулам (6.8), (6.10), если среднее значение показателя имеет тенденцию к росту.
можно использовать формулу (6.1), если среднее значение показателя за год меняется незначительно, или по формулам (6.8), (6.10), если среднее значение показателя имеет тенденцию к росту. . (6.13)
. (6.13) соответствует коэффициенту сезонности для того же месяца или квартала, но предыдущего года, например, делая прогноз на май 2015 года, необходимо использовать значение коэффициента сезонности, рассчитанное для мая 2014 года.
соответствует коэффициенту сезонности для того же месяца или квартала, но предыдущего года, например, делая прогноз на май 2015 года, необходимо использовать значение коэффициента сезонности, рассчитанное для мая 2014 года. ), а годовой объем производства – 200 шт. (
), а годовой объем производства – 200 шт. ( ), то трудоёмкость составит
), то трудоёмкость составит  часов. При использовании для изготовления изделий одних и тех же технологий величина нормы остаётся постоянной.
часов. При использовании для изготовления изделий одних и тех же технологий величина нормы остаётся постоянной. шт.
шт. руб. В том случае, когда хлеб не продается в день его завоза, магазин несёт убыток с каждой буханки:
руб. В том случае, когда хлеб не продается в день его завоза, магазин несёт убыток с каждой буханки:  руб. Если бы номинальная прибыль и потери, связанные с не реализацией хлеба были бы одинаковы, то ежедневная норма завоза хлеба была бы равна среднему объёму продаж за день, т.е. 135 буханок. Однако убыток, связанный с не реализацией превышает прибыль, получаемую в результате продажи буханки хлеба, а значит, норма завоза должна быть меньше 135 буханок.
руб. Если бы номинальная прибыль и потери, связанные с не реализацией хлеба были бы одинаковы, то ежедневная норма завоза хлеба была бы равна среднему объёму продаж за день, т.е. 135 буханок. Однако убыток, связанный с не реализацией превышает прибыль, получаемую в результате продажи буханки хлеба, а значит, норма завоза должна быть меньше 135 буханок. -вой буханки хлеба -
-вой буханки хлеба -  . Тогда ожидаемая прибыль, получаемая от реализации
. Тогда ожидаемая прибыль, получаемая от реализации  . (7.1)
. (7.1) , (7.2)
, (7.2) - вероятность того, что
- вероятность того, что  , или
, или 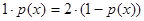 .
. .
.


 Вероятность
Вероятность






 1
1










 ,
, - коэффициент нормального распределения, зависящий от значения функции Лапласа –
- коэффициент нормального распределения, зависящий от значения функции Лапласа – 
 ;
; - среднее квадратическое отклонение, для нашего случая:
- среднее квадратическое отклонение, для нашего случая:
 .
.


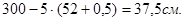
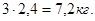 , в зависимости от того в какой размерности установлена цена на материал. Однако проанализируем возможность комбинации различных вариантов распила прутка.
, в зависимости от того в какой размерности установлена цена на материал. Однако проанализируем возможность комбинации различных вариантов распила прутка. - доля прутков, разрезаемых 3-м способом. Количество заготовок вида А и Б, а также долю
- доля прутков, разрезаемых 3-м способом. Количество заготовок вида А и Б, а также долю  ;
; .
. ,
,  и
и  .
. ,
,  , т.е. из 10 прутков можно вырезать по 22 заготовки каждого вида, а это - 11 изделий.
, т.е. из 10 прутков можно вырезать по 22 заготовки каждого вида, а это - 11 изделий. м.пог/шт, или
м.пог/шт, или  кг/шт.
кг/шт. ;
; .
. ,
,  и
и  .
. ,
,  , т.е. из 14 прутков можно вырезать по 30 заготовок каждого вида и, соответственно, получить 15 изделий.
, т.е. из 14 прутков можно вырезать по 30 заготовок каждого вида и, соответственно, получить 15 изделий. м.пог/шт, или
м.пог/шт, или  кг/шт.
кг/шт. м.пог/шт, или 6,55 кг/шт).
м.пог/шт, или 6,55 кг/шт). ,
,  и
и  , соответственно. Тогда по имеющимся данным за прошедшие месяцы (январь, февраль, март) можно составить следующую систему уравнений:
, соответственно. Тогда по имеющимся данным за прошедшие месяцы (январь, февраль, март) можно составить следующую систему уравнений:
 отсюда норма затрат на изготовление изделия А -
отсюда норма затрат на изготовление изделия А -  кВтч. Вычитая из третьего уравнения второе, имеем:
кВтч. Вычитая из третьего уравнения второе, имеем:  , и
, и  кВтч. Для вычисления постоянных затрат на освещение цеха подставим полученные величины норм
кВтч. Для вычисления постоянных затрат на освещение цеха подставим полученные величины норм  кВтч.
кВтч. .
. ) и вида Б (
) и вида Б ( ) получим плановые затраты электроэнергии.
) получим плановые затраты электроэнергии.








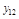








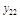







































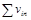

 и конечный продукт
и конечный продукт  для трехотраслевой экономической системы:
для трехотраслевой экономической системы:


 и нажав fx выбираем функцию МОБР:
и нажав fx выбираем функцию МОБР:

 .
.

 .
.




 , а матрица прямых затрат имеет вид:
, а матрица прямых затрат имеет вид: .
.


