
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повторные независимые испытанияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Схема испытаний Бернулли. Пусть опыт повторяется в неизменных условиях n раз. В каждом опыте некоторое событие А может наступить с вероятностью р и не наступить с вероятностью q = 1 – p. Вероятность того, что это событие наступит в n испытаниях ровно k раз вычисляется по формуле Бернулли:
Вероятности При больших значениях n пользуются приближенными формулами. Локальная формула Муавра – Лапласа. Если вероятность наступления некоторого события А в n независимых испытаниях постоянна, отлична от нуля и единицы, а число испытаний достаточно велико, причем npq ≥ 10, то вероятность
Значение Формула Пуассона. Точность приближенной формулы Муавра – Лапласа снижается по мере приближения вероятности р к нулю. В таких случаях пользуются приближенной формулой Пуассона. Если вероятность наступления каждого события в независимых испытаниях постоянна и мала, а число испытаний достаточно велико, причем npq < 10, то вероятность того, что в n независимых испытаниях событие наступит k раз находится по формуле:
где λ = nр. Интегральная формула Муавра-Лапласа. При больших значениях n вероятность того, что число появления события будет находиться в некотором интервале от k1 до k2 раз, вычисляют по интегральной формуле Муавра-Лапласа. Если вероятность наступления события А в каждом из n независимых испытаний постоянна, отлична от нуля и единицы
Наивероятнейшее число появления события в независимых испытаниях. Наивероятнейшее число появления события А в повторных независимых испытаниях (kо) определяется из неравенств:
Наивероятнейшее число kо – число целое. Если (np - q) – целое число, то имеется два наивероятнейших числа. Вероятность того, что в независимых испытаниях абсолютное отклонение относительной частоты от постоянной вероятности не превзойдет некоторого числа
1 Найти вероятность того, что при четырех подбрасываниях игральной кости 5 очков появится: а) два раза; б) хотя бы один раз; в) не менее 3 раз. 2 Всхожесть семян некоторого растения составляет 80 %. Найти вероятность того, что из пяти посеянных семян взойдут: а) пять семян; б) не менее четырех; в) не более одного. 3 Из 28 студентов группы 4 отличника. Наудачу вызываются три студента. Определить вероятности всех возможных значений числа отличников, которые могут оказаться среди вызванных трех студентов. 4 В семье 5 детей. Считая вероятности рождений мальчика и девочки одинаковыми, найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. 5 Вероятность того, что при сортировке изделий одно из них будет разбито, равна 0,005. Найти вероятность того, что из 200 изделий окажутся разбитыми: а) три изделия; б) не более двух; в) не менее двух изделий. 6 Станок автомат делает детали. Вероятность того, что деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется: а) четыре бракованных; б) не менее двух бракованных 7 Установлено, что вероятность обнаружения ошибки в каждом проверенном аудитором документе составляет 0,1. Определить вероятность того, что из 10 проверенных документов ошибка будет содержаться в одном. Вычислить по формулам Бернулли, Лапласа, Пуассона. Сравнить результаты, сделать выводы. 8 На факультете 900 студентов. Вероятность дня рождения каждого студента в данный день равна 9 Вероятность получения отличной оценки на экзамене равна 0,2. Найти наивероятнейшее число отличных оценок и вероятность этого числа, если сдают экзамен 100 студентов. 10 Вероятность того, что автомат при опускании одной монеты правильно сработает, равна 0,999. Найти наиболее вероятное число случаев неправильной работы автомата и вероятность этого числа случаев, если будет опущено 2000 монет. 11 Всхожесть клубней картофеля равна 80 %. Сколько нужно посадить клубней, чтобы наивероятнейшее число взошедших из них было равно 100?
12 Сколько раз нужно подбросить игральную кость, чтобы наивероятнейшее число выпадения 6 очков было равно 50? 13 Два равносильных противника играют в шахматы. Для каждого из них, что вероятнее выиграть: а) одну партию из двух или две из четырех; б) не менее двух партий из четырех или не менее трех партий из пяти. Ничьи во внимание не принимаются. 14 Бланк программированного опроса состоит из пяти вопросов. На каждый даны три ответа, среди которых один правильный. Какова вероятность, что методом угадывания студенту удастся выбрать по крайней мере четыре правильных ответа? 15 Вероятность того, что хотя бы одно изделие из 100 будет бракованным, составляет 0,1. Какой процент бракованных изделий выпускается предприятием. 16 При аудиторской проверке акционерного общества аудитор случайным способом отобрал 20 документов. Вероятность того, что документ имеет какую-то ошибку, равна 0,05. Определить вероятность того, что: а) только два документа будут содержать ошибку; б) хотя бы один документ будет содержать ошибку. Решить с помощью формул Бернулли и Пуассона и сравнить результаты. 17 Вероятность невыхода на работу из-за болезни равна 0,01 для каждого работника предприятия. Определить вероятность того, что в ближайший день не выйдет на работу хотя бы один из работников. Численность работников составляет 500 человек. 18 Вероятность успешной сдачи экзамена студентом составляет 0,8. Найти вероятность того, что из 100 студентов сдаст экзамен: а) 96 студентов; б) хотя бы 70 студентов; в) число сдавших экзамен составит от 70 до 90. 19 Известно, что 80 % специалистов в районе имеет высшее образование. Найти вероятность того, что из 100 наудачу отобранных человек высшее образование имеет: а) не менее 70; б) от 65 до 90 человек. 20 Вероятность заболевания гриппом в осенне-зимний период для населения поселка составляет 0,4. Найти вероятность того, что из 800 человек число заболевших составит: а) от 300 до 500 человек; б) более половины населения поселка. 21 Найти такое число k, чтобы с вероятностью 0,9 можно было утверждать, что среди 900 новорожденных более k мальчиков. Вероятность рождения мальчика 0,515. 22 В автопарке 70 машин. Вероятность поломки машины 0,2. Найти наиве- роятнейшее число исправных автомобилей и вероятность этого числа. 23 Всхожесть хранящегося на складе зерна равна 80 %. Определить вероятность того, что среди 100 зерен: а) число всхожих составит от 68 до 90 шт.; б) доля (частость) всхожих зерен будет отличаться от вероятности 0,8 по абсолютной величине не более чем на 0,1? 24 Два стрелка одновременно производят выстрелы по мишени. Сколько нужно произвести залпов, если наивероятнейшее число залпов, при которых оба стрелка попадут в мишень, равно 8? Вероятность попадания в мишень при одном выстреле первого стрелка равна 0,5, а второго – 0,8. 25 Вероятность выигрыша по лотерейному билету составляет 0,1. Сколько нужно купить билетов, чтобы с вероятностью 0,99 выиграл хотя бы один из них? 26 Два стрелка производят по n выстрелов, причем каждый стреляет по своей мишени. Определить вероятность того, что у них будет по одинаковому числу попаданий, если вероятность попадания при каждом выстреле постоянна и равна 0,5. 27 В автопарке имеется 400 автомобилей. Вероятность безотказной работы каждого из них равна 0,9. С вероятностью 0,95 определить границы, в которых будет находиться доля безотказно работавших машин в определенный момент времени.
28 Всхожесть зерна 90 %. Определить вероятность того, что для отобранных случайным образом 100 зерен относительная частота всхожести будет отличаться от вероятности взойти p = 0,9 по абсолютной величине не более, чем на 0,1. 29 Вероятность что случайно взятый избиратель проголосует за данного кандидата, составляет 0,4. Найти вероятность того, что: а) из 100 опрошенных избирателей более половины проголосует за данного кандидата: в) доля избирателей, проголосовавших за данного кандидата, будет отклоняться от постоянной вероятности не более чем на 0,05? 30 Отдел контроля проверяет на стандартность 900 деталей. Вероятность того, что деталь стандартна, равна 0,9. С вероятностью 0,9544 найти границы, в которых будет заключено число стандартных деталей. 31 Известно, что 10 % делянок под овощами плохо обработано. Сколько нужно проверить делянок, чтобы с вероятностью 0,9973 можно было утверждать, что относительная частота засоренных делянок будет отличаться от вероятности засоренности по модулю не более чем на 0,01? 32 Для определения степени поражения винограда вредителями было обследовано 400 кустов. Вероятность поражения куста виноградника равна 0,03. Определить границы, в которых с вероятностью 0,9545 будет заключено число кустов, не пораженных вредителями. 33 По экспертной оценке, доля семей (р) с очень высокими доходами составляет 0,1. Каков должен быть объем выборки, чтобы с вероятностью не менее 0,99, погрешность в оценке доли семей с высокими доходами была не более 0,0025? 34 Страховая компания заключила 5000 договоров определенного вида. Вероятность страхового случая по каждому из них в течение года составляет 2 %. Найти: а) вероятность того, что в течение года страховых случаев будет не более 120: б) наивероятнейшее число страховых случаев; в) вероятность того, что абсолютная величина отклонения доли договоров со страховым случаем, будет отклоняться от постоянной вероятности не более чем на 0,5 %.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.92 (0.007 с.) |

 . (3.1)
. (3.1) , где к = 0, 1, …, n, называются биноминальными вероятностями.
, где к = 0, 1, …, n, называются биноминальными вероятностями. , где
, где  . (3.2)
. (3.2) при заданном значении x находят по таблице (приложение 1), причем
при заданном значении x находят по таблице (приложение 1), причем  , а при x > 5, φ(x) = 0.
, а при x > 5, φ(x) = 0. , (3.3)
, (3.3) , а число испытаний достаточно велико, то вероятность того, что в n испытаниях событие произойдет от k1 до k2 раз, определяется по формуле:
, а число испытаний достаточно велико, то вероятность того, что в n испытаниях событие произойдет от k1 до k2 раз, определяется по формуле: где
где  (3.4)
(3.4) - функция Лапласа,
- функция Лапласа,  ; (3.5)
; (3.5)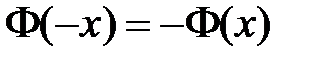 , при х > 5, Ф(х) = 0,5.
, при х > 5, Ф(х) = 0,5.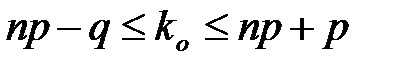 . (3.6)
. (3.6) , определяется по формуле:
, определяется по формуле: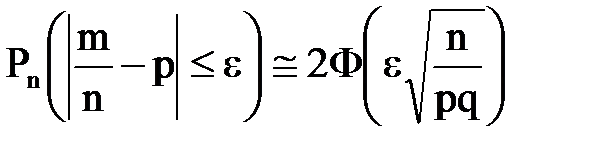 . (3.7)
. (3.7) . Найти вероятность того, что найдутся три студента с одним и тем же днем рождения.
. Найти вероятность того, что найдутся три студента с одним и тем же днем рождения.


