
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повторение независимых испытаний. Схема БернуллиСодержание книги
Поиск на нашем сайте
Самой простой моделью повторения испытаний являются независимые испытания, в каждом из которых вероятность появления некоторого события При больших где или формула Пуассона Можно рекомендовать пользоваться теоремой Лапласа, если Если требуется найти вероятность того, что в
Для функций Значение
Если
Пример 1. Вероятность попадания в мишень при каждом выстреле равна 0,6. Какова вероятность того, что при четырех выстрелах будет ровно три попадания. Решение. Воспользуемся формулой Бернулли. По условию задачи
Пример 2. Вероятность попадания в объект равна 0,75. Для разрушения объекта необходимо не менее трех попаданий. Произведено пять выстрелов. Какова вероятность того, что объект будет разрушен? Решение. Вероятность события
Пример 3. Вероятность сбоя в работе телефонной станции при каждом вызове равна 0,012. Поступило 1000 вызовов. Какова вероятность 9 сбоев? Решение. Так как число опытов
По таблице находим Окончательно Пример 4. Вероятность выхода из строя за время Решение. Для этой задачи математической моделью является схема Бернулли. Здесь Согласно теореме Муавра-Лапласа
Тогда
7. δ-функция и ее свойства Пусть
Функционал
Всюду в дальнейшем в качестве линейного пространства
Примеры линейных функционалов на а) Всякая кусочно-непрерывная функция
б) Такой функционал, который любой функции По аналогии с а) действие
Последнее равенство называют фильтрующим свойством Производной функционала Так как Отметим следующие свойства
Равенство справедливо для любой функции
В частности, при
|
|||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 384; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.165.234 (0.007 с.) |

 постоянна и равна
постоянна и равна  . Тогда вероятность того, что в
. Тогда вероятность того, что в 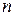 опытах событие
опытах событие 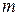 раз, определяется формулой Бернулли
раз, определяется формулой Бернулли  где
где 

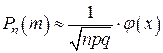 ,
,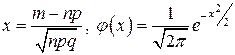
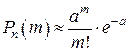 . Здесь
. Здесь 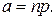
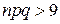 , и формулой Пуассона, если
, и формулой Пуассона, если  .
.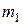 , но не более чем
, но не более чем 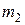 раз, то используют формулы
раз, то используют формулы ,
,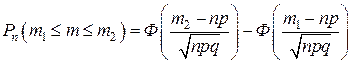 , где
, где 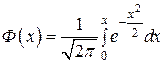 ,
,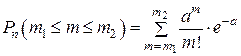 .
.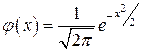 и
и 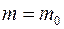 , при котором вероятность
, при котором вероятность  принимает наибольшее значение, называется наивероятнейшим числом успехов.
принимает наибольшее значение, называется наивероятнейшим числом успехов. , где
, где  – символ целой части числа.
– символ целой части числа.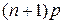 – целое число, то
– целое число, то  принимает два значения.
принимает два значения. ,
,  .
. Следовательно,
Следовательно,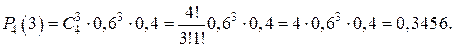



 велико и
велико и 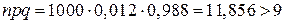 , то воспользуемся локальной теоремой Лапласа
, то воспользуемся локальной теоремой Лапласа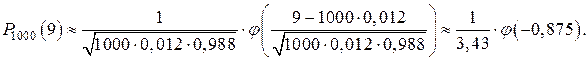
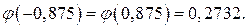
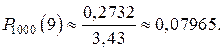
 одного конденсатора равна 0,2. Определить вероятность того, что за время
одного конденсатора равна 0,2. Определить вероятность того, что за время 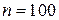 ,
, 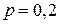 ,
, 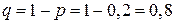 ,
, 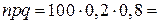
 .
.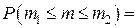
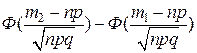 ,
,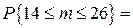
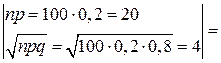
 .
. – линейное пространство. Отображение
– линейное пространство. Отображение  , то есть правило, согласно которому всякому
, то есть правило, согласно которому всякому 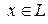 ставится в соответствие число, называется функционалом.
ставится в соответствие число, называется функционалом.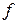 называется линейным, если для любых
называется линейным, если для любых 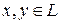 и любых чисел
и любых чисел  и
и 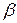
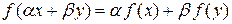 .
.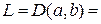 {
{ 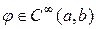 ,
, 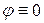 вблизи концов интервала}. То есть
вблизи концов интервала}. То есть  – это линейное пространство бесконечно дифференцируемых функций, определенных на интервале
– это линейное пространство бесконечно дифференцируемых функций, определенных на интервале  , тождественно равных нулю вблизи концов этого интервала. Действие функционала
, тождественно равных нулю вблизи концов этого интервала. Действие функционала  ,
,  будем записывать так:
будем записывать так: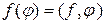 .
.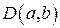
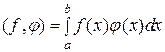
 .
.
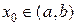 .
.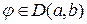 ставит в соответствие значение этой функции в точке
ставит в соответствие значение этой функции в точке 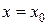 , называется
, называется  - функцией.
- функцией.
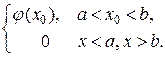
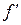 , действующий по правилу
, действующий по правилу 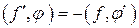 ,
,  .
.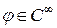 , то любой функционал имеет бесконечное количество производных и
, то любой функционал имеет бесконечное количество производных и 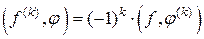 .
. - функции:
- функции: Если
Если 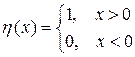 – функция Хевисайда, то
– функция Хевисайда, то  .
.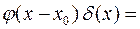
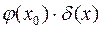 .
. .
.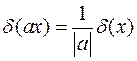 .
. ,
, 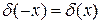 .
.


