
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства плотности распределения вероятности непрерывной случайной величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1) 2) 3) 4) Замечание. Для функции распределения
где
Для случайных величин вводят понятия начальных и центральных моментов, из которых наиболее часто используются математическое ожидание и дисперсия. Математическим ожиданием случайной величины
Говорят, что математическое ожидание у случайной величины существует, если ряд (интеграл) (1) сходится абсолютно. Дисперсией случайной величины
Дисперсия вычисляется по формулам:
Рассеивание возможных значений случайной величины от её математического ожидания часто характеризуют средним квадратическим отклонением Существует достаточно большое число законов распределения дискретных и непрерывных величин, которые встречаются в приложениях. Параметры этих законов являются числовыми характеристиками случайных величин или же числовые характеристики выражаются через параметры законов распределения.
Примеры распределений дискретных случайных величин
Примеры распределений непрерывных случайных величин
Запись
Здесь Пример 1. Изделия испытываются при перегрузочных режимах. Вероятности для каждого изделия пройти испытания, равны 0,8. Испытания заканчиваются после первого же изделия, не выдержавшего испытания. 1. Найти закон распределения вероятностей (ряд распределения) для числа испытаний (случайной величины 2. Построить многоугольник распределения. 3. Найти функцию распределения и построить её график. 4. Найти: а) Решение. Введем в рассмотрение случайную величину Случайная величина Закон распределения вероятностей будет иметь вид
Для построения многоугольника распределения в декартовой прямоугольной системе координат построим точки
3. Функция распределения Для решаемой задачи Строим график функции распределения
4. а)
б) в) Пример 2. Дискретная случайная величина Решение. Для дискретной случайной величины В данном случае
Пример 3. Дискретная случайная величина Решение. Обозначим третье возможное значение случайной величины через
Пример 4. Плотность распределения вероятностей случайной величины
Найти параметр Решение. Значение параметра
Пример 5. Поток заявок, поступающих на телефонную станцию, представляет собой простейший поток. Математическое ожидание числа вызовов за час равно 30. Найти вероятность того, что за минуту поступит не менее двух вызовов. Решение. Так как поток заявок представляет собой простейший поток, то число заявок, поступающих на телефонную станцию, распределено по закону Пуассона
с математическим ожиданием Следовательно, для решаемой задачи Обозначим через
= Пример 6. Случайная величина Найти вероятность Решение. Известно, что математическое ожидание и дисперсия пуассоновского распределения совпадают и равны значению его пара-метра
решениями которого являются числа
Для искомой вероятности получаем
Известно, что Пример 7. Время безотказной работы некоторого узла сложного агрегата – экспоненциальная случайная величина со средним Решение. По условию задачи
Известно, что математическое ожидание экспоненциальной случайной величины есть величина, обратная параметру: Таким образом, вероятность отказа узла в течение 10 часов будет равна Если запараллелено
Искомое значение
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 504; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.213.76 (0.01 с.) |

 .
. .
. в любой точке непрерывности
в любой точке непрерывности  .
.

 .
. дискретной случайной величины справедлива формула
дискретной случайной величины справедлива формула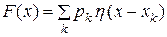 ,
, функция Хэвисайда. Дифференцируя последнее равенство, видим, что и для дискретной случайной величины можно ввести плотность распределения вероятности по формуле
функция Хэвисайда. Дифференцируя последнее равенство, видим, что и для дискретной случайной величины можно ввести плотность распределения вероятности по формуле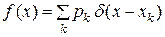 .
. называется число
называется число (1)
(1) называется число
называется число .
.
 для дискретной случайной величины.
для дискретной случайной величины.
 для непрерывной случайной величины, где
для непрерывной случайной величины, где  .
.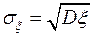 .
. Биномиальное распределение
Биномиальное распределение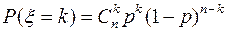
 ,
, 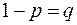 ,
,  ,
, ,
,  .
.
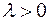 ,
,  ,
,  ,
,  .
.
 ,
,  .
. )
) ,
,  ,
,  ,
,  ,
, 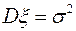 .
. означает, что случайная величина
означает, что случайная величина  распределена нормально с параметрами
распределена нормально с параметрами  и
и  .
.
 ,
, 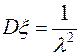 .
.
 ,
, 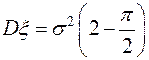 .
. ,
, 


 – гамма-функция:
– гамма-функция: 

 ).
). , б)
, б)  , в)
, в)  .
. число изделий, прошедших испытания. Очевидно, что случайная величина
число изделий, прошедших испытания. Очевидно, что случайная величина 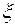 может принимать значения от 1 и, теоретически, до бесконечности.
может принимать значения от 1 и, теоретически, до бесконечности. , если осуществится событие, состоящее в том, что
, если осуществится событие, состоящее в том, что  изделия пройдут испытания, а
изделия пройдут испытания, а  – вероятность того, что изделие пройдет испытание, а
– вероятность того, что изделие пройдет испытание, а  – вероятность того, что изделие не пройдет испытание, то по теореме умножения вероятностей случайных событий,
– вероятность того, что изделие не пройдет испытание, то по теореме умножения вероятностей случайных событий, 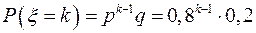 , где
, где  .
.
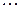





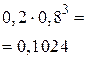
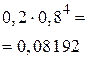
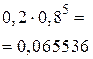

 и соединим их ломаной.
и соединим их ломаной.




 .
. ,
,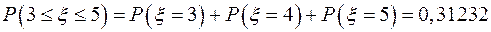 .
. ,
, 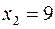 ,
,  . Вероятности этих значений соответственно равны
. Вероятности этих значений соответственно равны  ,
,  ,
,  . Найти математическое ожидание
. Найти математическое ожидание  , дисперсию
, дисперсию  и среднее квадратическое отклонение
и среднее квадратическое отклонение 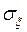 .
.
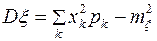 .
.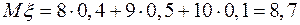 .
.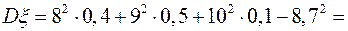
 .
. .
. . Вероятности этих значений соответственно равны
. Вероятности этих значений соответственно равны  . Найти закон распределения случайной величины
. Найти закон распределения случайной величины  .
. . Так как для дискретной случайной величины
. Так как для дискретной случайной величины  , то
, то 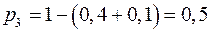 . Значение
. Значение  , то есть из уравнения
, то есть из уравнения  . Решив уравнение, найдем
. Решив уравнение, найдем  . Составим закон распределения
. Составим закон распределения


 , функцию распределения вероятностей случайной величины
, функцию распределения вероятностей случайной величины  ,
,  ,
,  .
.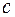 найдем из условия нормировки
найдем из условия нормировки  . Для заданной
. Для заданной  это условие примет вид
это условие примет вид  . Интегрируя, получим
. Интегрируя, получим  , откуда
, откуда  . Следовательно
. Следовательно 
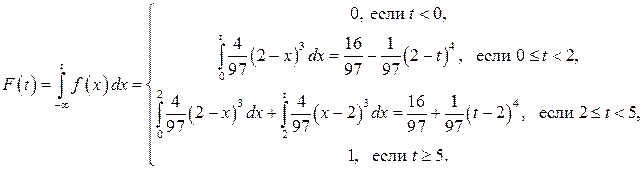
 .
. .
. .
.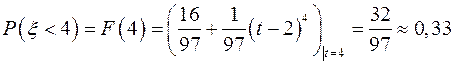 .
.
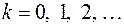 ,
,  ,
, .
.
 событие, состоящее в том, что за минуту поступит не менее двух вызовов. Тогда
событие, состоящее в том, что за минуту поступит не менее двух вызовов. Тогда

 =
=
 .
.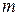 и дисперсия
и дисперсия 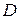 связаны соотношением
связаны соотношением  .
. ,
,  .
. . Условие задачи приводит к уравнению относительно
. Условие задачи приводит к уравнению относительно  ,
, ,
,  . Последнее значение не может быть параметром пуассоновского распределения в силу положительности параметра. Таким образом, случайная величина
. Последнее значение не может быть параметром пуассоновского распределения в силу положительности параметра. Таким образом, случайная величина  ,
,  .
.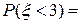





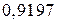 .
. . Из этого равенства
. Из этого равенства  . Для заданной случайной величины
. Для заданной случайной величины  ,
,  . Следовательно,
. Следовательно,  .
. . Для увеличения надежности агрегата узел дублируется – ставят параллельно несколько одинаковых, но функционирующих независимо узлов. Сколько узлов следует запараллелить, чтобы с вероятностью, не меньшей чем 0,9, по крайней мере один из них не вышел из строя за 10 часов работы?
. Для увеличения надежности агрегата узел дублируется – ставят параллельно несколько одинаковых, но функционирующих независимо узлов. Сколько узлов следует запараллелить, чтобы с вероятностью, не меньшей чем 0,9, по крайней мере один из них не вышел из строя за 10 часов работы?

 . По условию задачи
. По условию задачи  , следовательно,
, следовательно,  .
.

 .
. идентичных узлов, то событие
идентичных узлов, то событие  {по крайней мере один из узлов не выйдет из строя за 10 часов} является противоположным событию
{по крайней мере один из узлов не выйдет из строя за 10 часов} является противоположным событию 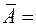 {все узлы выйдут из строя за 10 часов}. Поэтому,
{все узлы выйдут из строя за 10 часов}. Поэтому,  . Узлы работают независимо, поэтому по теореме умножения вероятностей независимых событий
. Узлы работают независимо, поэтому по теореме умножения вероятностей независимых событий .
.



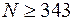 .
.


