
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальное распределение случайной величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нормальное распределение часто используется для описания случайных явлений, в которых на результат измерения влияет большое число независимых случайных факторов. Определение. Случайная величина ξ имеет нормальное или гауссовскоераспределение, еслиее плотность распределения вероятностей при всех x задается равенством
Отметим некоторые свойства графика этой функции (кривой нормального распределения). Во-первых, функция Во-вторых, функция В-третьих, асимптотой кривой нормального распределения является ось О х. Особую роль играет нормальное распределение с параметрами m= 0, σ= 1, которое часто называют стандартным (или нормированным) нормальным распределением. Плотность стандартного нормального распределения имеет вид
Функция распределения случайной величины, имеющей нормальный закон, может быть представлена в виде несобственного интеграла F(x) = Функцию распределения стандартного нормального закона Ф(х) = часто называют функцией Лапласа, для которой имеются таблицы значений, широко используемые в статистических исследованиях. Рассмотрим свойства нормального распределения. Свойство 1. Пусть случайная величина ξ имеет нормальное распределение с параметрами m и σ,т.е. M (ξ)= m; D( ξ)=σ2. Свойство 2. Между функциями распределения F(x) и
Таблицы значений функции Свойство 3. При любых значениях x имеет место равенство
Следующее свойство позволяет вычислить вероятность попадания случайной величины в интервал, используя таблицы значений функции Свойство 4. Пусть случайная величина ξ имеет нормальное распределение с параметрами m и σ, т.е.
В частности, для симметричного интервала относительно m имеет место формула для любого
Формула (2.36) непосредственно следует из (2.35), в которой надо положить
Свойство 5 (закон трех сигм). Пусть случайная величина ξ имеет нормальное распределение с параметрами m и σ,т.е. Действительно, по свойству 4,
Биномиальное распределение Биномиальное распределение служит вероятностной моделью для многих явлений. Рассмотрим последовательность n независимых испытаний Бернулли, в каждом из которых может произойти один из двух исходов. Обозначим через p вероятность «успеха» в отдельном испытании и - q вероятность «неудачи». Для каждого отдельного испытания i введем случайную величину Отсюда следует, что случайная величина η может принимать возможные значения m= 0,2,…, n. Вероятность того, что случайная величина η после завершения всех испытаний примет значение m можно найти по формуле Бернулли P (η =m) = Определение. Случайная величина η имеет биномиальное распределение с параметрами n и p, если она принимает значения, m= 0, 1,…, n с вероятностями по формулам (2.38). Вычислим математическое ожидание и дисперсию случайной величины, имеющей биномиальное распределение. Из формулы (2.20) и свойств математического ожидания и дисперсии для суммы несовместных случайных величин следует, что
Математическое ожидание и дисперсия случайной величины M (xi)=1 p+ 0 q=p, D (xi)=12 p+ 02 q – p 2 =pq. Для случайной величиныη, имеющей биномиальное распределение с параметрами n и p, математическое ожидание и дисперсия имеют вид: M (η)= np, D (η) =npq. Пример 2.9. В коробке находятся 3 однотипных изделия, при этом каждое может быть или бракованным, или стандартным. Рассмотрим случайную величину, которая определяет число бракованных изделий в коробке. «Успехом» отдельного испытания будем считать наличие в коробке некоторого числа бракованных изделий. Тогда случайная величина x может принять значения x 1 = 0, x 2=1, x 3=2, x 4=3 (варианты количества бракованных изделий)и имеет биномиальное распределение. Требуется найти вероятности событий, которые будут соответствовать значениям случайной величины. Последовательно при i= 0, 1, 2, 3из формулы (2.38) получим вероятности для возможных значений этой случайной величины: p 1 =P (x = 0)= p 3 =P (x = 2) = Теперь можно записать таблицу для ряда распределения:
Математическое ожидание и дисперсию находим по формулам (2.21) и (2.23) соответственно M (x)=3 p, D (x)=3 p q.
Распределение Пуассона Определение. Случайная величина x распределена по закону Пуассона с параметром распределения l>0, если она принимает значения m = 0,1, 2,… с вероятностями pm = P (x =m) = Пример 2. 10. Рассмотрим случайную величину x,равную числу покупателей, посетивших супермаркет в промежутке времени от t 0 до T. Появление покупателей - случайные события и происходят в случайные моменты времени. Сделаем следующие предположения. 1. Вероятность появления одного покупателя за малый промежуток времени
где 2. Если за малый промежуток времени 3. События на непересекающихся промежутках времени являются независимыми случайными величинами. В этих условиях можно доказать, что число покупателей, посетивших супермаркет в промежутке времени от t 0 до T распределено по закону Пуассона с параметром
Вопросы для самопроверки 1. Как вычислить математическое ожидание и дисперсию: а) для дискретной случайной величины? б) для непрерывной случайной величины? 2. Как найти плотность вероятности для случайной величины, имеющей равномерное распределение? 3. Что такое нормально распределенная случайная величина? 4. Какие другие законы распределения известны?
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 686; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.89.70 (0.007 с.) |


 . (2.29)
. (2.29) Числа m и σ называются параметрами распределения: параметр m может быть любым действительным числом: -∞ < m < + ∞, а параметр σ – положительным:σ>0. Символическая запись
Числа m и σ называются параметрами распределения: параметр m может быть любым действительным числом: -∞ < m < + ∞, а параметр σ – положительным:σ>0. Символическая запись  означает, что cлучайная величина ξ имеет нормальное распределение с параметрами m и σ2.
означает, что cлучайная величина ξ имеет нормальное распределение с параметрами m и σ2.
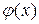 принимает максимальное значение
принимает максимальное значение  при x=m.
при x=m. , (2.30) Ниже приведен график y = f 0(x).
, (2.30) Ниже приведен график y = f 0(x).
 . (2.31)
. (2.31) (2.32)
(2.32) имеет место следующее соотношение
имеет место следующее соотношение . (2.33)
. (2.33) . (2.34)
. (2.34) . Тогда вероятность попадания случайной величины ξ в интервал [ a,b ] можно найти по формуле
. Тогда вероятность попадания случайной величины ξ в интервал [ a,b ] можно найти по формуле . (2.35)
. (2.35) :
: . (2.36)
. (2.36) и использовать свойство, что
и использовать свойство, что 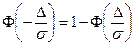 . Тогда получим
. Тогда получим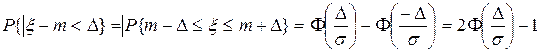 .
.
 . Из таблицы функций
. Из таблицы функций 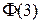 =0,9987. Отсюда следует, что
=0,9987. Отсюда следует, что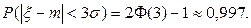
 , которая может принимать два значения: 1, если испытание закончилось «успехом» и 0, если – «неудачей». Случайная величина η - число «успехов» при n независимых испытаниях в схеме Бернулли будет равна сумме независимых случайных величин
, которая может принимать два значения: 1, если испытание закончилось «успехом» и 0, если – «неудачей». Случайная величина η - число «успехов» при n независимых испытаниях в схеме Бернулли будет равна сумме независимых случайных величин  , т.е.
, т.е.  . (2.37)
. (2.37) , m= 0, 1, …, n. (2.38)
, m= 0, 1, …, n. (2.38) ,
, .
.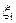 будут соответственно равны
будут соответственно равны ; p 2 =P (x = 1)=
; p 2 =P (x = 1)=  ;
; ; p4 =P (x = 3) =
; p4 =P (x = 3) =  .
. , m = 0,1,2,… (2.39)
, m = 0,1,2,… (2.39) пропорциональна
пропорциональна  а > 0,
а > 0, - бесконечно малая величина при
- бесконечно малая величина при  .
.




