
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интервальная оценка дисперсии нормального распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Построим доверительный интервал для дисперсии D=σ2 наблюдаемой случайной величины Введем случайную величину (статистику) которая согласно утверждению 2 теоремы Фишера имеет распределение
Обычно доверительный интервал
Тогда условия для определения значений
По таблице квантилей
Рис. 3.9. Неравенства
Следовательно, интервал
является доверительным интервалом дисперсии, соответствующим доверительной вероятности β. Пример 3.3. По данным выборочного контроля найти выборочное математическое ожидание и несмещенную оценку дисперсии нормальной случайной величины ξ. Найти доверительные интервалы для них, соответствующие доверительной вероятности β=0,98. Таблица 3.4
Решение. Выборочное математическое ожидание найдем по формуле (3.14), используя табл.3.4 При Несмещенную выборочную дисперсию вычислим по формуле (3.19):
Доверительный интервал для математического ожидания определим по формуле (3.35). При получим искомый доверительный интервал для математического ожидания:
Границы доверительного интервала для дисперсии определим по формуле (3.20). По таблице квантилей распределения χ2 (см. табл. С Приложения) при
Подставив эти значения, а также
Вопросы для самопроверки 2. Что называется выборкой? 3. Как произвести оценку выборочного математического ожидания и выборочной дисперсии? 4. Как найти функцию распределения для дискретной случайной величины? 5. Что такое несмещенная оценка параметра? 6. Дайте определение состоятельной оценки. 7. Что такое интервальная оценка?
Заключение В результате изучения выше приведенного материала студент может приступить к выполнению контрольной работы и проверить свои ответы на вопросы самоконтроля. Затем после выполнения лабораторных работ может приступить к ответам на вопросы экзаменационного теста и получить оценку за проделанную работу.
Глоссарий Биномиальное распределение с параметрами n и p – вычисление вероятности того, что случайная величина принимает значения m= 0, 1,…, n. Вариационный ряд – последовательность элементов выборки, расположенных в неубывающем порядке (одинаковые элементы записываются последовательно друг за другом). Вероятность произведения двух независимых событий – произведение вероятностей этих событий. Вероятность события -- отношение числа исходов m события А к общему числу элементарных событий N. Возможные значения случайной величины – числа ¦(w). Выборка – последовательность значений из генеральной совокупности; - объема k -часть, состоящая из k элементов генеральной совокупности; - репрезентативная – позволяет адекватно описать случайную величину - случайная объема n – последовательность n независимых случайных величин из генеральной совокупности. Выборочная дисперсия – величина, равная сумме квадратов разностей между значением случайной величины и ее математическим ожиданием, деленная на объем выборки. Выборочное среднее – число, равное сумме значений случайной величины, деленной на объем выборки. Генеральная совокупность – конечная или бесконечная совокупность наблюдений над случайной величиной. Геометрическое определение вероятности – отношение площади S (A), соответствующей событию A, к площади всей области W. Гипергеометрическое распределение – вычисление вероятности того, что случайная величина примет заданное значение через число сочетаний. Гипотеза альтернативная – гипотеза, конкурирующая с основной; -основная – гипотеза, которая проверяется; -статистическая – предположение относительно параметров или закона распределения случайной величины. Гистограмма – представление статистического ряда на плоскости. Дискретная случайная величина -множество возможных значений образует конечную или бесконечную последовательность чисел, т.е. конечно или счетно. Дисперсия случайной величины x – момент второго порядка случайной величины (x - M (x)). Доверительная вероятность – вероятность, с которой производится оценка параметров. Доверительный интервал – область значений, при которых основная гипотеза принимается. Дополнение множества A – разность между всем множеством S и множеством А, которое является частью S. Достоверное событие W – всегда наступает в условиях данного эксперимента. Закон трех сигм – значения случайной величины ξ, имеющей нормальное распределение с параметрами m и σ,содержатся в интервале Кривая распределения – график плотности вероятности. Критерий значимости – вероятность ошибки 1-го рода. Критерий - согласия – правило, в соответствии с которым принимается решение; - Колмогорова – проверка гипотезы о совпадении функций распределения. Математическое ожидание дискретной случайной величины x – сумма ряда из произведений возможных значений xi на их вероятности pi. Множество – некоторая совокупность объектов, называемых элементами множества. Множество конечное – состоящие из конечного числа элементов, в противном случае – бесконечное множество.
Момент второго порядка случайной величины x – математическое ожидание квадрата этой случайной величины. Моргана формулы или соотношения двойственности – правило для записи выражения, соответствующего «отрицанию» функции. Невозможное событие – это такое, которое не может наступить в условиях данного эксперимента, т.е. это событие имеет пустое множество благоприятствующих исходов. Независимые с обытия A и B– событие А происходит независимо от того, происходит событие В или нет. Несовместные события A и B– не могут происходить одновременно. Нормальное или гауссовское распределение – случайная величина ξ имеет плотность распределения вероятностей при всех x
- хи-квадрат (Пирсона) – проверка гипотезы о совпадении дисперсий. Относительная частота события A – показывает долю опытов, в которых наступило событие A при N экспериментах. Оценка интервальная – доверительный интервал: - несмещенная – математическое ожидание случайной величины в этом случае равно оцениваемому параметру; - точечная – произвольная функция элементов выборки, когда параметр неизвестен. Ошибка второго рода – событие, состоящее в том, что гипотеза принимается, когда на самом деле она неверна. Ошибка первого рода – событие, состоящее в том, что гипотеза отвергается, когда на самом деле она верна. Показательное распределение с параметром Произведение или пересечение множеств A и B– множество, состоящее из всех общих элементов этих множеств. Пространство элементарных событий – множество всех исходов данного эксперимента. Противоположное событие – это событие, которое происходит в том случае, если не происходит событие А. Пустое множество – множество, не содержащее элементов. Равномерное распределение -случайная величина ξ на промежутке [ a,b ] имеет постояннуюплотность распределения вероятностей. Размещение из n элементов по k элементов – упорядоченные выборки объема k без возвращения элементов. Разность множеств A и B – множество, состоящее из всех элементов множества A, которые не содержатся в множестве B. Ряд распределения – статистический ряд, записанный в виде таблицы. Случайная величина – функция f, которая каждому элементарному событию w ставит в соответствие число ¦(w). Событие – некоторое высказывание о результатах рассматриваемого эксперимента. Сочетание из n элементов по k элементов - неупорядоченные выборки объема k без возвращения элементов. Стандартное или средне-квадратическое отклонение -квадратный корень из дисперсии. Статистика – результат наблюдения над случайной величиной. Статистический ряд – последовательность различных значений, расположенных в возрастающем порядке, с указанием относительных частот. Сумма или объединение множеств A и B – множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств. Уровень значимости статистического критерия – величина, определяющая степень достоверности вычислений. Условие нормировки – площадь криволинейной трапеции под всей кривой распределения равна 1. Условная вероятность – вероятность события A при условии, что событие B произошло. Функция Лапласа - функция распределения стандартного нормального закона. Функция распределения F(x) случайной величины x -вероятность того, что случайная величина примет значение, меньшее заданного х. Частный случай – если при каждом осуществлении события A происходит и событие B, то говорят, что событие A влечет событие B. Частота события A – число экспериментов mn (A), в которых наступило событие A. Элементарные события – исходы (результаты) эксперимента. Эмпирическая функция распределения – относительная частота события, заключающегося в том, что случайная величина примет значение, меньшее чем заданное число.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 ~
~  по случайной выборке
по случайной выборке  при неизвестном математическом ожидании.
при неизвестном математическом ожидании. , (3.36)
, (3.36) с
с  степенями свободы. Поскольку плотность распределения этого закона асимметрична, доверительный интервал, соответствующий надежности β, найдем из формулы (3.31) в виде:
степенями свободы. Поскольку плотность распределения этого закона асимметрична, доверительный интервал, соответствующий надежности β, найдем из формулы (3.31) в виде: . (3.37)
. (3.37) для случайной величины
для случайной величины  .
. и
и  будут иметь вид:
будут иметь вид: ,
,  . (3.38)
. (3.38) ,
,  . (3.39)
. (3.39)
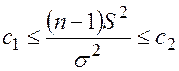 эквивалентны неравенствам
эквивалентны неравенствам  , поэтому
, поэтому .
. (3.40)
(3.40)


 .
. ,
,  .
. из таблицы А Приложения находим квантиль распределения Стьюдента
из таблицы А Приложения находим квантиль распределения Стьюдента  . Вычислив предельную ошибку
. Вычислив предельную ошибку  ,
, .
. ,
,  .
. и
и 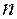 в формулу (3.20), получим искомый доверительный интервал для дисперсии
в формулу (3.20), получим искомый доверительный интервал для дисперсии .
.

 .
. – это такоераспределение, плотность вероятности которого задается равенством
– это такоераспределение, плотность вероятности которого задается равенством 



