Вычисление числовых характеристик распределений вероятностей

Числовыми характеристиками распределения вероятностей случайных величин, позволяющими наглядно получить представление о том или ином распределении, являются моменты и квантили.

Первым моментом случайной величины является математическое ожидание или среднее значение, которое характеризует центр распределения вероятностей.

Вторым моментом, характеризующим разброс случайной величины относительно математического ожидания, является центральный момент случайной величины, который называют дисперсией. Величина, равная корню квадратному из дисперсии, называется среднеквадратическим отклонением.

Для случайных величин, принимающих вещественные значения, используются такие характеристики, как квантили.

Квантилью Хр случайной величины, имеющей функцию распределения F(x), называется решение Хр уравнения F(x) - р, где р - заданная вероятность.

Среди квантилей чаще всего используют медиану и квартили распределения.

Медианой называется квантиль, соответствующий значению р = 0,5. Верхним квартилем называется квантиль, соответствующий значению р = 0,75, а нижним - квантиль, соответствующий значению р = 0,25.

В табличном процессоре для вычисления некоторых числовых характеристик дискретных распределений вероятностей используются функции СРЗНАЧ, ДИСПР, СТАНДОТКЛОНП, КВАРТИЛЬ и ПЕРСЕНТИЛЬ:

СРЗНАЧ(число_1; число_2;...) - предназначена для вычисления математического ожидания всей совокупности значений дискретной случайной величины;

ДИСПР(число_1; число_2;...) - вычисляет дисперсию дискретного распределения;

СТАНДОТКЛОНП(число_1; число_2;...) - позволяет оценить стандартное отклонение дискретного распределения;

КВАРТИЛЬ(массив; значение) - позволяет определить квартами распределения. Параметр массив представляет собой диапазон ячеек содержащий значения дискретной случайной величины или сами значения, а параметр значение определяет, какой квартиль должна быть вычислен (0 - минимальное значение распределения, 1 - нижний квартиль, 2 - медиана, 3 - верхний квартиль, 4 - максимальное значение распределения).

ПЕРСЕНТИЛЬ (массив; К) - позволяет вычислить р - квантили распределения. Параметр массив представляет собой диапазон ячеек, содержащий значения дискретной случайной величины или сами значения, параметр К - значение персентиля (от 0 до 1).

Пример 2.3 Дан набор случайных значений случайной величины 10, 14, 5, 6, 10, 12, 13. Требуется вычислить математическое ожидание, дисперсию, стандартное отклонение, верхний квартиль и квантиль со значением 0,1.

Решение

1.В диапазон ячеек рабочего листа (В2:В7) введем заданные числа.

2.Оформим таблицу, как показано на рисунке 2.4.

3.Используя приведенные выше статистические функции, вычислим требуемые числовые характеристики.

Рис. 2.4

 

ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТИ ОТДЕЛЬНЫХ ЗНАЧЕНИЙ
СЛУЧАЙНЫХ ВЕЛИЧИН

Табличный закон распределения

Напомним, что соответствие между отдельными возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины. Закон распределения дискретной случайной величины может быть задан таблицей 2.1.

Таблица 2.1

X	X1	X2	…	xn
P	P1	P2	…	pn

При распределении, заданном таблично, математическое ожидание вычисляется по формуле

М(х)= х₁ р₁ + х₂р₂ +...+ Р х_пр_п.

Дисперсия дискретной случайной величины вычисляется по формуле

D(X) = М(Х²) - [М(Х)]².

Среднеквадратичное отклонение дискретной случайной величины вычисляется по формуле .

Пример 2.4 Вероятностный прогноз для величины X - процентного изменения стоимости акций по отношению к текущему курсу в течение 6 месяцев дан в виде закона распределения

Таблица 2.2

№
X
Р	0,1	0,1	0,2	0,3	0,2	0,1

Требуется вычислить вероятность того, что покупка акций будет более выгодна, чем помещение денег на банковский депозит под 3% за месяц сроком на 6 месяцев.

Решение

Вычислим в MS Excel прирост суммы по депозиту за шесть месяцев.

Таблица 2.3

С17	f(x)
	А	В
		Прирост по депозиту
		=1+0,03
		=В2*0,03+В2
		=В3*0,03+63
		=В4*0,03+В4
		=В5*0,03+85
		=В6*0,03+В6
	прирост	=В7-1

 

	С17	f(x)
	А В
	Прирост по депозиту
		103,00%
		106,09%
		109,27%
		112,55%
		115,93%
		119,41%
	прирост	19,41%

Прирост суммы за 6 месяцев составит 19,41%.

Вероятность того, что покупка акций выгоднее депозита, определяется суммой вероятностей, соответствующих курсу акций более 19,41% и равна Р(Х> 19,41) = PA +P5 + Р6 - 0,3 + 0,2 + 0,1 = 0,6.

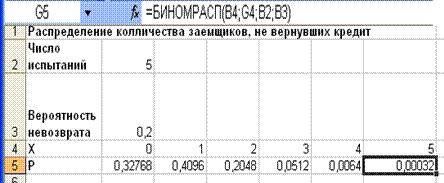
Биноминальное распределение

Биноминальное распределение - одно из самых распространенных дискретных распределений, которое служит моделью для многих процессов.

Для вычисления вероятности отдельного значения биноминального распределения или значения случайной величины по заданной вероятности в табличном процессоре есть функции БИНОМРАСП и КРИТБИНОМ.

Функция БИНОМРАСП применяется для вычисления вероятности в задачах с фиксированным числом испытаний или тестов, когда результатом любого испытания может быть только успех или неудача.

Функция имеет параметры:

БИНОМРАСП(число_успехов; число_испытаний; вероятность_успеха; интегральная),

где

число_успехов - количество успешных испытаний;

число_испытаний - количество независимых испытаний;

вероятность_успеха - вероятность успеха каждого испытания;

интегральная - логическое значение, определяющее форму функции. Если аргумент имеет значение ИСТИНА, то функция возвращает интегральную функцию распределения, т.е. вероятность того, что число успешных испытаний не менее значения аргумента число успехов. Если этот аргумент имеет значение ЛОЖЬ, то вычисляется значение функции плотности распределения, т.е. вероятность того, что число успешных испытаний равно значению аргумента число успехов.

Функция КРИТБИНОМ служит для вычисления наименьшего числа успешных исходов случайной величины, для которого интегральное биноминальное распределение больше или равно заданной величине (критерию).

Функция имеет параметры: КРИТБИНОМ(число_испытаний; вероятность_успеха; альфа),

где число_испытаний - количество независимых двухальтернативных испытаний; вероятность успеха - вероятность успеха каждого испытания;

альфа - значение критерия, которое является уровнем значимости.

Paсмотрим на примерах технологию применения приведенных функций.

Пример 2.5 Банк выдает пять кредитов. Вероятность невозврата кредита для каждого из заемщиков. Составить таблицу закона распределения количества заемщиков, не вернувших кредит по окончании срока кредитования.

Решение

1. На рабочем листе подготовим исходные данные для расчета:

—в ячейку А2 введем текст «Число испытаний», а в ячейку В2 - количество выданных кредитов - число 5 (рис. 2.5);

—в ячейку A3 введем текст «Вероятность невозврата», а в ячейку ВЗ - значение вероятности невозврата кредита - число 0,2;

—в ячейку А4 введем текст «X» - обозначающий случайную величину;

—в диапазоне B4:G4 построим последовательность членов арифметической прогрессии от 0 до 5;

—в ячейку А5 введем текст «Р», обозначающий вероятность невозврата кредита.

2. Установим курсор в ячейку В5. Выполним команду меню Вставка/Функция. В открывшемся окне диалога выберем категорию Статистические и функцию БИНОМРАСП.

3. В соответствующие поля диалогового окна Аргументы функции (рис. 2.6) введем значения аргументов функции, делая ссылки на соответствующие ячейки, содержащие исходные данные. Аргументу Интегральная установим значение 0, что соответствует тому, что вероятность числа успешных испытаний будет равна значению аргумента Число успехов.

4. Установим для соответствующих аргументов абсолютные адреса, используя клавишу <F4>.

5. Скопируем полученную формулу в диапазон C5:G5. В ячейках диапазона В5:С5 будет вычислен результат.

6. По данным полученной таблицы построим график (рис. 2.7).

Из таблицы и графика следует, что вероятность невозврата четырех и пяти кредитов очень мала, а вероятность невозврата одного кредита является самой большой и составляет величину 0,4096.

 

 

Рис. 2.5

Рис. 2.6

 

Рис. 2.7

 

Пример 2.6 Для условий задачи предыдущего примера найти значение числа невозвращенных кредитов, для которого вероятность интегрального распределения Р >= 0,4.

Решение

1. Установим курсор в свободную ячейку рабочего листа. Выполним команду меню Вставка/Функция. В открывшемся окне диалога Выберем категорию Статистические и функцию КРИТБИНОМ.

2. В окне Параметры функции введем значения параметров: число_испытаний - 5, вероятность_успеха - 0,2, альфа - 0,4.

После выполнения вычислений в ячейке будет получен результат равный единице. Таким образом, при вероятности интегрального распределения P>=0,4 будет не менее одного успешного события, т.е. невозвращенных кредитов будет не менее одного. Это также можно увидеть из графика примера 2.5.

Пример 2.7 Построить диаграмму биноминальной функции плотности вероятности Р(А = т) при п = 10 и р= 0,2.

Решение

1. Диапазон рабочего листа (АЗ:А13) заполним возможными значениями исходов испытаний: 0, 1, 2,..., 10.

2. Установим курсор в ячейку ВЗ и выполним команду меню Вставка/Функция. В открывшемся окне диалога выберем категорию Статистические и в списке функций - БИНОМРАСП.

3. В диалоговом окне Параметры функции БИНОМРАСП заполним поля параметров.

Число_успехов - введем количество успешных испытаний т, для чего щелкнем на ячейке A3;

Число_испытаний - введем общее количестве; проведенных испытаний - 10;

Вероятность_ycnexa - введем величину вероятности успеха в каждом испытании 0,2;

Интегральная - введем вид функции распределения 0 - весовая.

После щелчка на кнопке ОК в ячейке ВЗ будет вычислена вероятность р = 0,1073774 того, что из всех десяти испытаний будут все неудачные.

4. Скопируем формулу из ячейки ВЗ во все ячейки диапазона B4:В13.

Полученную таблицу оформим так, как изображено на рисунке, построим гистограмму плотности вероятности (рис. 2.8).

Рис. 2.8