Технология решения задач регрессионного анализа

Важную роль при исследовании взаимосвязей между статистическими выборками кроме корреляционного и дисперсионного анализа играет регрессионный анализ. Регрессия позволяет проанализировать воздействие на какую-либо зависимую переменную одной или более независимых переменных и позволяет установить аналитическую форму (модель) этой зависимости в виде аппроксимирующего полинома.

Если рассматривается зависимость между одной зависимой переменной у и несколькими независимыми х₁, х₂,..., х_п, то речь идет о множественной линейной регрессии. В этом случае уравнение регрессии имеет вид

у = а₀ + а₁х₁+а₂х₂+…+a_nx_n,

где а₁, а₂,…, а_п - коэффициенты при независимых переменных, которые нужно вычислить (коэффициенты регрессии); а_о - константа. При построении регрессионной модели важнейшими моментами являются оценка ее адекватности (эффективности) и значимости, на основании которых можно судить о возможности применения в практике полученной модели.

Мерой оценки адекватности регрессионной модели является коэффициент детерминации R² (R-квадрат), который определяет, с какой степенью точности полученное уравнение регрессии аппроксимирует исходные данные.

Значимость регрессионной модели оценивается с помощью критерия Фишера (F-критерия). Если величина f-критерия значима (р < 0,05), то регрессионная модель является значимой.

В табличном процессоре можно аппроксимировать экспериментальные данные линейным уравнением до 16-го порядка

у = а₀ + а₁х₁+а₂х₂+…+a₁₆x_16.

Для вычисления коэффициентов регрессии служит инструмент Регрессия, который можно включить следующей последовательностью операций.

1. Выполнить команду Сервис/Анализ данных.

2. В раскрывшемся окне диалога Анализ данных выбрать из списка строку Регрессия - раскроется окно диалога Регрессия.

3. В группе Входные данные в поле Входной интервал у указать адресную ссылку ми диапазон, содержащий значения зависимой переменной, а в поле Входной интервал X- ссылку на диапазон, содержащий переменных, т.е. переменных, влияние которых на зависимую переменную у оценивается. Установить флажок Метки, если исходная таблица имеет названия столбцов и фла­ок Константа-ноль, если а₀ = 0.

4.В группе Параметры выхода указать адресную ссылку на ячейку рабочего листа, которая будет являться верхней левой ячейкой результирующей таблицы.

Если необходимо получить визуальную картинку отличия экспериментальных точек от предсказанных регрессионной моделью, то установить флажок График подбора.

Если нужно получить график нормальной вероятности, то установить флажок График нормальной вероятности.

В выходном диапазоне после выполнения вычислений отображаются результаты дисперсионного анализа, коэффициенты регрессии, стандартная погрешность вычисления у, среднеквадратичные отклонения, количество наблюдений, стандартные погрешности для коэффициентов.

Значения коэффициентов регрессии размещаются в столбце Коэффициенты:

- у - пересечение а₀;

- х₁, - коэффициент а₁;

- х₂ - коэффициент а₂ и т.д.

В столбце Р-Значение содержится оценка достоверности отличия соответствующих коэффициентов от нуля. Если Р > 0,05, то коэффициент можно считать нулевым. Это означает, что соответствующая независимая переменная практически не влияет на зависимую переменную.

Значение R-квадрат определяет, с какой степенью точности регрессионное уравнение будет аппроксимировать экспериментальные данные.

Если R-квадрат > 0,95, то точность аппроксимации высокая.

При 0,8 < R-квадрат < 0,95 аппроксимация удовлетворительная.

В случае когда R-квадрат < 0,6 точность аппроксимации недостаточна и модель требует улучшения.

Кроме инструмента Регрессия в табличном процессоре для получения параметров уравнения регрессии есть функция ЛИНЕЙН и функция ТЕНДЕНЦИЯ для получения значения у в требуемых точках.

 

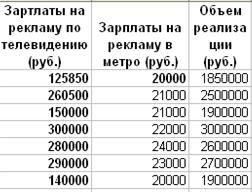
Пример 2.16 Имеются статистические данные о затратах, связанных с рекламой по телевидению, с рекламой в метро и объеме реализации продукции в рублях, приведенные в таблице. Требуется найти регрессионные коэффициенты для независимых переменных Расходы на рекламу по телевидению и Расходы на рекламу в метро на объем реализации продукции и построить уравнение регрессии.

Решение

1. На рабочем листе в диапазон А1:С8 введем данные приведенной таблицы 2.9.

Таблица 2.9

 

1.Включим инструмент Регрессия.

В открывшемся диалоговом окне Регрессия установим параметры (рис. 2.24)

 

Рис. 2.24

 

- Входной интервал у - диапазон С1:С8;

- Входной интервал х - диапазон А1:В8;

- Флажок Метки;

- Выходной интервал - адрес D1;

- Флажок График нормальной вероятности;

- Флажок График остатков.

После щелчка на кнопке ОК в диапазон D1:L21 будет выведен результат регрессионного анализа (рис. 2.25).

 

Рис. 2.25