Вычисление корней функции одной переменной

Корнями функции Y=f(x) называют такие значения х, при которых функция принимает значения ноль.

Процесс нахождения корней функции, как правило, осуществляется в два этапа.

На первом этапе отделяются корни, т.е. находятся такие отрезки, внутри которых находится строго один корень.

На втором этапе производится уточнение корней, т.е. находят их значение с заданной точностью (). В практических задачах решением является значение х, отличающееся по модулю от точного значения не более чем на величину .

При решении практических задач величина х являются каким-либо ресурсом, величина которого ограничена и лежит в области допустимого диапазона значений. Поэтому при решении задачи интерес представляют только те корни, которые находятся в области возможных значений х.

Отделение корней функции в ограниченной области определения переменной х в табличном процессоре можно выполнить, используя ее табличную или графическую модель.

Для отделения корней функции нужно выполнить следующие операции:

- табулировать функцию, задавая значения аргумента в диапазоне допустимых значений аргумента;

- построить график функции и определить, где находятся точки пересечения графика функции с осью х;

- в полученной табличной модели найти ближайшие приближения к значениям корней. Ближайшими приближениями являются те значения аргумента, в промежутке между которыми значение функции изменяет знак.

Уточнение значений корней можно выполнить с помощью одного из двух инструментов - Подбор параметра или Поиск решения, Оба эти инструмента используют итерационные методы и позволяют получить результат с заданной точностью. Для уточнения корней с пoмощью инструмента Подбор параметра нужно выполнить следующие операции.

1.Выполнить настройку табличного процессора, для этого:

- выполнить команду меню Сервис/Параметры;

- в открывшемся диалоговом окне Параметры выбрать закладке Вычисления;

- в открывшемся диалоговом окне Вычисления установить флажок Итерации, в поле Предельное число итераций установить нужное число итераций, в поле Относительная погрешность ввести величину относительной погрешности вычислений;

- щелкнуть на кнопке ОК.

2. Используя инструмент табличного процессора Подбор параметра, вычислить корни уравнения с заданной точностью.

Рассмотрим технологию вычисления корней функции на примере.

 

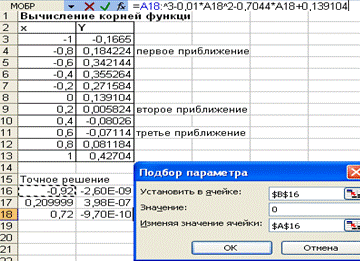
Пример 1.17 Найти все корни функции

у = х³ - 0,01х² - 0,7044х + 0,139104 в диапазоне значений аргумента [-1; 1].

 

Решение

Заданная функция представлена полиномом третьей степени, следовательно, она может иметь не более трех корней.

Для локализации начальных приближений определим интервалы значений X, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [-1;+1] с шагом 0,2, получим табличные значения функции. Просмотрев полученную таблицу, находим, что график функции трижды пересекает ось X, следовательно, исходное уравнение имеет на заданном отрезке все три корня.

Анализ таблицы показывает, что функция меняет знак в следующих интервалах значений аргумента Х: (-1;-0,8), (0,2;0,4) и (0,6;0,8), следовательно, корни функции лежат внутри этих интервалов. Поэтому в качестве начальных приближений возьмем значения X: -0,8; 0,2 и 0,6.

На свободном участке рабочего листа в диапазон ячеек (А16:А18) введем начальные приближения, а в соответствующие ячейки столбца введем формулу, реализующую функциональную зависимость.

Выполним команду меню Сервис/Параметры, во вкладке Вычисления открывшегося диалогового окна установим относительную погрешность вычислений = 0,000001, а число итераций N = 1000, установим флажок Итерации.

Выполним команду меню Сервис/Подбор параметра. В диалоговом окне заполним следующие поля:

- Установить в ячейке: в поле укажем адрес ячейки, в которой записана формула правой части функции (В16);

- Значение: в поле укажем значение, которому должно удовлетворять значение функции, т.е. правая часть уравнения (в нашем случае 0 ),

- Изменяя значение: в поле укажем адрес ячейки (где записано начальное приближенное А16), в которой будет вычисляться корень уравнения и на которую ссылается формула. После щелчка на кнопке ОК в ячейке А16 получим значение первого корня: -0,92.

5. Выполняя последовательно операции аналогичные предыдущим, вычислим значения остальных корней: -0,209991 и 0,720002 (рис.1.23).

 

 

 

 

 

Рис. 1.23

 

Решение уравнений

В предыдущем параграфе рассмотрена технология вычисления корней функции одной переменной. Предположим, что требуется решить уравнение х² - 4 = 0,

т.е найти такие значения х, при которых левая часть выражения, представленная полиномом второй степени, обращается в ноль. Представим уравнение в виде функциональной зависимости у = х² - 4.

Нетрудно догадаться, что решениями уравнения будут корни полученной функции.