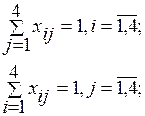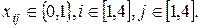Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Технология Решения задач дискретного программированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Цель: научиться решать задачи дискретного программирования.
Теоретическое введение Дискретное программирование изучает экстремальные задачи, в которых на искомые переменные накладывается условие дискретности, а область допустимых решений конечна. Это, прежде всего, задачи с физической неделимостью многих факторов и объектов расчета. К дискретному программированию относят также ряд задач целочисленного программирования, в которых искомые переменные принимают только целочисленные значения (например, задача о планировании) или логические, булевы, значения – нуль или единица. Рассмотрим решение задачи дискретного программирования на транспорте. В автотранспортном предприятии для перевозок пассажиров используются автобусы различной вместимости. Каждый из автобусов, работая по заданному маршруту, может перевести определенное количество пассажиров. Почасовая оплата сij i-му водителю по j-му виду перевозок приведена в табл. 6.1. Составить план работы водителей таким образом, чтобы все плановые перевозки были выполнены, каждый водитель работал только по одному маршруту, а суммарная стоимость почасовой оплаты была минимальной. Таблица 6.1 Стоимость выполнения работ
Решение задачи сводится к реализации следующих этапов: 1. Проверка задачи на сбалансированность. 2. Построение математической модели задачи. Пусть хij = 1 в случае работы i-м водителем по j-му маршруту и xij = 0 в случае отсутствия перевозок по маршруту. Тогда математическая модель задачи примет вид: целевая функция
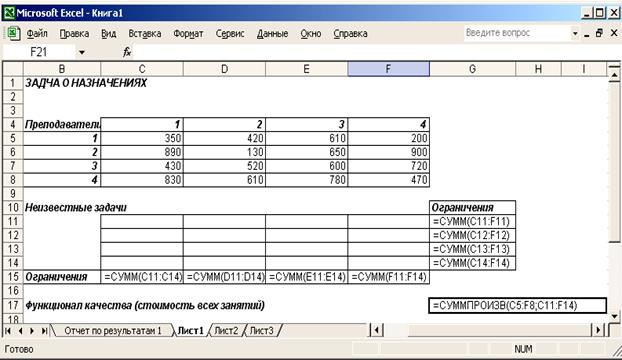
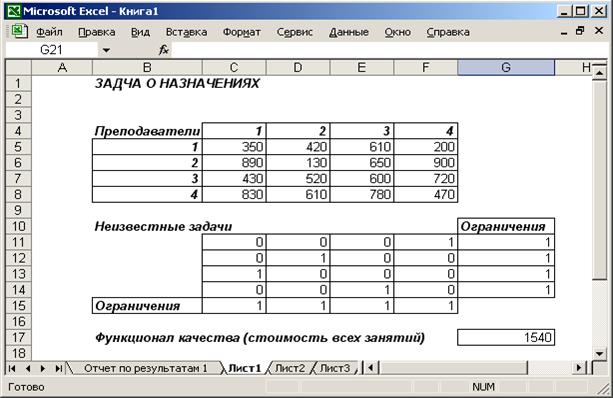
3. Решение задачи с помощью надстройки Поиск решения: - подготовка рабочего листа (рис. 6.1), формулы для расчета представлены в табл. 6.2; Таблица 6.2 Формулы для расчета в задаче о назначениях
Рис. 6.1. Подготовка рабочего листа для решения задач
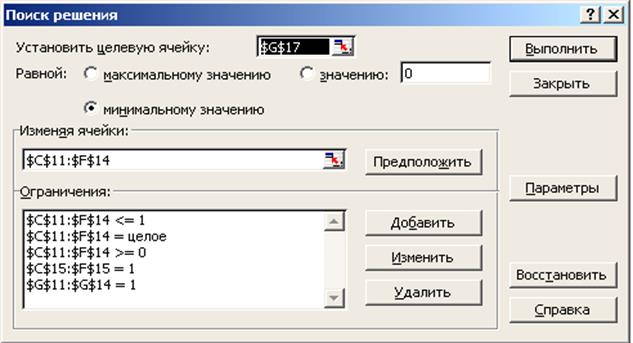
- установка ограничения в окне Поиск решения, как показано на рис. 6.2. Решение задачи представлено на рис. 6.3.
Рис. 6.2. Установка параметров в окне Поиск решения для задачи дискретного программирования
Рис. 6.3. Решение задачи о назначениях
Задания для практической работы Имеется n водителей и m маршрутов движения автобусов. Стоимость сij работы i-м водителем по j-му маршруту приведена в таблицах вариантов. Составить план выполнения перевозок таким образом, чтобы все перевозки были выполнены, каждый водитель работал только на одном маршруте, а суммарная стоимость перевозок была минимальной. Задания представлены в соответствующих таблицах по вариантам [4].
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 11
Вариант 12
6.3. Контрольные вопросы 1. Что изучает дискретное программирование? 2. Укажите этапы решения задач дискретного программирования. 3. Что такое целевая функция? 4. В чем заключается подготовка рабочего листа для решения задач? 5. Как осуществляется установка параметров в окне Поиск решения для задачи дискретного программирования? 6. Укажите основные этапы решения задачи о назначениях.
ГЛОССАРИЙ Диапазон ячеек рабочего листа - область, включающая смежные ячейки рабочего листа, которая имеет адрес или имя. Генератор случайных чисел - инструмент, входящий в пакет анализа табличного процессора, предназначенный для генерации массивов чисел, распределенных по различным законам. Компьютерная модель - модель, которая реализуется и исследуется на компьютере, с использованием соответствующих инструментов и технологий. Консолидация - объединение данных из одной или нескольких таблиц с выполнением необходимых расчетов. Макрос - программа на языке программирования, оформленная как процедура SUB, выполняющая заданную последовательность операций на рабочем листе. Массив - набор данных одного типа. Математическая модель - модель объекта или процесса, заданная аналитическими выражениями (математическими формулами) Модель - прототип реального объекта либо процесса, который адекватно отражает только те свойства реального процесса или объекта, которые существенны для исследования или для решения задачи. Поиск решения - инструмент, включенный в надстройки табличного процессора, который вычисляет заданное значение функции путем подбора значений ее аргументов. Целевая функция - функция, которая оптимизируется путем подбора ее аргументов. Linux - открытая операционная система, альтернативная ОС Microsoft Windows.
Список литературы
1. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: учеб. пособие. М..: Финансы и статистика, 2010. 2. Гарнаев А.Ю. Использование MS Excel и VBA в экономике и финансах. – С-Пб.: БХВ – Санкт-Петербург, 2010. – 336 с. 3. Гельман В.Я. Решение математических задач средствами Excel: практикум. СПб.: Питер, 2011. 4. Геращенко И.П. Экономико-математические методы и модели: учебное пособие /И.П. Геращенко, Е.В. Шульга. – Омск: Изд-во Омского экономического института, 2009. – 292 с. 5. Гусева О.Л., Миронова Н.Н. Excel для Windows. Практические работы //Информатика и образование. – 2009. – №2–6. 6. Елисеева И.И. Практикум по эконометрике: учеб. пособие / И.И. Елисеева, С.В. Курышева и др.; под ред. И.И. Елисеевой. М.: Финансы и статистика, 2012. 7. Ильченко А.Н. Экономико-математические методы: учеб. пособие. М.: Финансы и статистика, 2011. 8. Красе М.С., Чупрынов Б.П. Математика для экономистов. СПб.: Питер, 2008 (Серия «Учебное пособие»). 9. Кутуков В.Б. Основы финансовой и страховой математики: Методы расчета кредитных, пенсионных, инвестиционных и страховых схем. М.: Дело, 2010. 10. Матвеев Л.А. Компьютерная поддержка решений. – С-Пб.: Специальная литература, 2010. – 472 с. 11. Овчаренко Е.К., Ильина О.П., Балыбердин Е.В. Финансово-экономические расчеты в Excel. Изд. 3-е. – М.:Филинъ, 2009. – 328 с. 12. Рудикова Л. В. Microsoft Excel для студента / Л.В. Рудикова. – СПб.: БХВ - Петербург, 2009. – 368 с
Учебное издание
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 673; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.007 с.) |

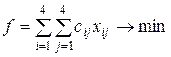 при ограничениях
при ограничениях