
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Суммирование и вычитание матрицСодержание книги
Поиск на нашем сайте
Суммой матриц А и В одинаковой размерности называется матрица С такой же размерности, каждый элемент которой равен сумме соответствующих элементов матрицы А и В. Например, если
А =
Пример 1.5 Сложить матрицы А = Решение Введем значения элементов матрицы А в диапазон А2:С3, а элементы матрицы В – в диапазоне D2:E3. Выделим диапазон, где будут размещаться элементы результирующей матрицы С, например G2:H3. В выделенном диапазоне введем формулу =A2:B3+D2:E3. Нажмем комбинацию клавиш <Ctrl>+<Shift>+<Enter>. После выполнения операций выполнения в диапазоне ячеек G2:H3 будут помещены результаты вычислительных значений элементов результирующей матрицы С (рис.1.5.).
Рис. 1.5
Подобным образом вычисляют разность матриц, а также их скалярное произведение (деление). В библиотеке Excel в категории математических функций есть функции для выполнения операций над матрицами, список которых приведен в таблице 1.1. Все перечисленные функции, кроме функции ТРАНСП, размещены в Мастере функций в группе Математические функции. Функция ТРАНСП находится в группе функций Ссылки и массивы. Параметрами функций, приведенных в таблице могут быть адресные ссылки и массивы, содержащие значения элементов матриц, или имена диапазонов, например МОБР(А1:В2), или МОПР(Матрица_А) (табл1.1.). Таблица 1.1 Встроенные функции MS Excel для работы с матрицами
Вычисление произведения матриц Произведение матриц может быть вычислено, если количество столбцов умножаемой матрицы равно количеству строк матрицы множителя. Если А = (аij) имеет размерность т x п, и В=(bij) с размерностью п
Вычисление произведения матриц в табличном процессоре выполняется с помощью специальной функции рабочего листа, имя которой МУМНОЖ. Она имеет синтаксис:
МУМНОЖ(Массив1; Массив2), где Массив1 - адрес диапазона, в котором записаны элементы первой матрицы; Массив2 - адрес диапазона, в котором записаны элементы второй матрицы. Пример 1.6 Умножить матрицу А=
Рис. 1.6 Решение систем линейных уравнений Метод обратной матрицы Система т линейных уравнений с п неизвестными х1, х2,..., хn имеет вид
Матрица А называется матрицей системы.
Свободные и неизвестные члены представляются в виде матриц-столбцов
В матричной форме система линейных уравнений записывается в виде А В частном случае, когда число уравнений в системе (m) равно числу неизвестных (n), т.е. т = n, то решение такой системы можно найти и методом обратной матрицы в виде Х=А-1 Технологию решения системы линейных уравнений методом обратной матрицы рассмотрим на примере. Пример 1.7 Система уравнений задана матрицами А=
Присвоим диапазону А3:В4 имя (например, А) и введем в ячейки значения элементов матрицы А. Присвоим диапазону D3:D4 имя (например, В) и введем значения элементов вектора В. Выделим область F3:F4 для помещения результата решения системы и введем в него формулу =МУМНОЖ(МОБР(А);В). Нажмем комбинацию клавиш <Ctrl> + <Shift> + <Enter>, в ячейках диапазона F3:F4 будет получен результат (рис.1.7.).
Рис. 1.7 Чтобы выполнить проверку полученных результатов, достаточно перемножить исходную матрицу на вектор результата, итогом этой операции является массив, содержащий такие же значения, как и вектор В. При решении некоторых задач в электронной таблице в формулах удобно использовать ссылки на имена ячеек или диапазонов. Имя - это идентификатор. Область действия имени - вся рабочая книга. Для присвоения имени диапазону молено применить два приема: —выделить диапазон и в поле имени записать идентификатор; —выполнить команду меню Вставка/Имя/Присвоить. В открывшемся окне в поле Имя ввести идентификатор имени, а в поле Формула записать адрес диапазона (лучше в виде абсолютного адреса. Для установки абсолютного адреса используйте клавишу <F4c>.
Метод наименьших квадратов Технология решения систем линейных уравнений для случая, когда т= п, рассмотрена выше. Однако в общем случае т может быть не всегда равно п. Возможны три случая: т < п, т = п. и т > п. При т < п, если система является совместной, то она не определена и имеет бесконечное множество решений. В случае если т>п система совместна, то матрица А имеет по крайней мере т- п линейно независимых строк. В этом случае решение может быть получено отбором п любых линейно независимых уравнений и применением формулы х =А-1 Затем обе части уравнения нужно умножить на (АТА)-1. Если эта матрица существует, то система определена. С учетом того, что (АTА)-1 Рассмотрим технологию решения систем линейных уравнений методом наименьших квадратов на примере. Пример 1.8 Требуется решить систему уравнений:
Решение Введем значения элементов матрицы А в диапазон ячеек рабочего листа (А2:В4). Введем значения элементов вектора В в ячейки рабочего листа, например D2:D4. Транспонируем исходную матрицу, для чего выделим диапазон ячеек размерность 3 =ТРАНСП(А2:В4). Нажмем комбинацию клавиш <Ctrl> + <Shift> + <Enter> - в ячейках выделенного диапазона будут помещены элементы транспонированной матрицы. Вычислим произведение АTА, для чего выделим диапазон (А9:В10) и введем в него формулу =МУМНОЖ(А6:С7;А2:В4). Вычислим произведение АТВ, для чего выделим диапазон из двух ячеек (Е6:Е7) и введем в него формулу =MУMHОЖ(A6:C7;D2:D4). Выделим диапазон (D9:E10), введем в него формулу =МОБР(А9:В10) для вычисления обратной матрицы (АтА)-1. Матрица существует, следовательно, исходная система определена. Для вычисления итогового результата - решения системы уравнений выделим диапазон (В12:В13) и введем в него формулу умножения матриц (АТА)-1 =МУМНОЖ(D9:Е10;А9:В10). Нажмем комбинацию клавиш <Ctrl> + <Shift> + <Enter> - в ячейках диапазона В12:В13 будет получен результат решения системы (рис.1.8.).
Рис. 1.8 При достаточно хорошем навыке работы с Мастером функций приведенную задачу можно решить без промежуточных вычислений, как это рассмотрено выше, а введя сразу все выражение для вычисления в строку формул. Рассмотрим эту технологию более подробно на том же примере. Формула, которая дает решение системы X = (АТА)-1
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.171 (0.009 с.) |

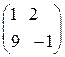 и В =
и В =  , то С =
, то С =  .
.
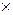 р, то матрица С, полученная умножением матрицы А на матрицу В, будет иметь размер т
р, то матрица С, полученная умножением матрицы А на матрицу В, будет иметь размер т 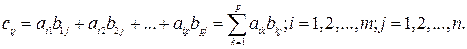
 на матрицу В=
на матрицу В=  . Решение в электронной таблице приведено на рис. 1.6.
. Решение в электронной таблице приведено на рис. 1.6.



 В=
В=  . Требуется решить заданную систему линейных уравнений.
. Требуется решить заданную систему линейных уравнений.
 Решение
Решение





