Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение технологии при решении макроэкономических задачСодержание книги
Поиск на нашем сайте
Известно, что рациональное функционирование многоотраслевого хозяйства предполагает соблюдение баланса между отраслями. Каждая отрасль многоотраслевого хозяйства является, с одной стороны, производителем определенной продукции, а с другой - потребителем продукции, выпускаемой другими отраслями. Макроэкономика функционирования многоотраслевого хозяйства требует, чтобы соблюдался баланс по производству и потреблению между отдельными отраслями. Балансовый принцип связи различных отраслей состоит в том, что валовой выпуск i-й отрасли должен быть равен сумме объемов потребления. В простейшей форме балансовые соотношения имеют вид xi=xi1+xi2+…+xin + yi, i=1, 2, …, n, где Xi - общий объем выпускаемой продукции i-й отрасли; Xij- объем продукции i-й отрасли, потребляемый j-й отраслью при производстве объема продукции xj. Yi - объем продукции i-й отрасли конечного потребления (для реализации в непроизводственной сфере). Для производства продукции j-й отрасли объемом хi, нужно использовать продукцию i-й отрасли объемом аijxi, где аij - постоянное число, характеризующее прямые затраты. Это допущение позволяет представить модель многоотраслевой экономики (модель Леонтьева) в виде системы линейных уравнений, которая в матричной форме имеет
где
А - матрица коэффициентов прямых затрат. Приведенная система уравнений может быть представлена в виде (Е - А) Если существует обратная матрица (Е - А)-1 (матрица полных затрат), то существует единственное решение системы - матрица А продуктивна тогда и только тогда, когда матрица (Е-А)-1 существует и ее элементы неотрицательны; - матрица А с неотрицательными элементами продуктивна, если сумма элементов по любому ее столбцу (строке) не больше единицы, Причем хотя бы для одного столбца (строки) строго меньше единицы. Рассмотрим пример решения макроэкономической задачи на применение модели Леонтьева. Пример 1.11 Втаблице 1.4. приведены данные по балансу за некоторый период времени между пятью отраслями. Таблица 1.4
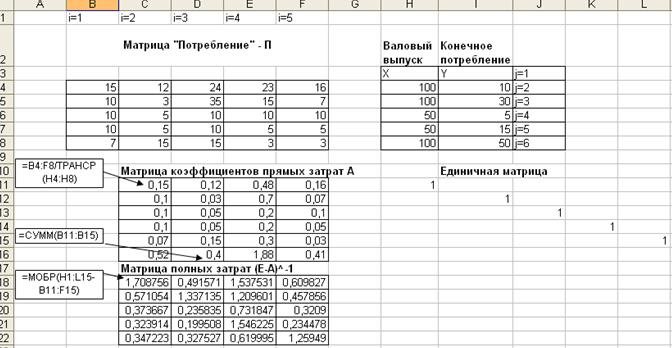
Требуется найти векторы конечного потребления и валового выпуска, а также матрицу коэффициентов прямых затрат и определить ее продуктивность. В приведенной таблице в первых пяти столбцах (группа «Потребление») содержатся значения хij в последнем столбце содержатся элементы вектора валового выпуска Решение В диапазон ячеек рабочего листа (B4:F8) введем числа, записанные в столбцах «Потребление», исходной таблицы (рис. 1.13). Введем в ячейки диапазона (Н4:Н8) значения элементов вектора валового выпуска X, который соответствует последнему столбцу исходной таблицы, а в диапазон (I4:I8) - значения элементов вектора Y- вектор конечного продукта. Матрица коэффициентов прямых затрат А вычисляется путем деления i-го столбца матрицы «Потребление» на i-ю строку вектора X. Это вычисление можно выполнить, используя формулу А = П: XT, где П - матрица «Потребление». Выделим диапазон ячеек, в котором будет размещаться матрица А и введем в него формулу деления массива «Потребление» на транспонированный вектор X: =B4:F8/TPAHCП(H4:H8) и нажмем комбинацию клавиш <Ctrl> + <Shift> + <Enter>. После выполнения этой операции в выделенном диапазоне будут вычислены значения элементов матрицы коэффициентов прямых затрат А. Просуммируем столбцы полученной матрицы А. Вычислим значения элементов матрицы полных затрат. Проанализируем полученные в результате расчетов данные. Матрица полных затрат (Е - А)-1 существует, все ее элементы положительны. Следовательно, первое условие продуктивности матрицы А выполняется. Все элементы матрицы А положительные, однако в третьем и четвертом столбцах их суммы превышают значение единицы, следовательно второе условие продуктивности матрицы А не выполняется. Таким образом, матрица коэффициентов прямых затрат в решаемой задаче непродуктивна (рис. 1.12.).
Рис. 1.12
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 223; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.163 (0.006 с.) |

 ,
,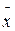 - вектор валового выпуска;
- вектор валового выпуска; - вектор объема продукции конечного потребления;
- вектор объема продукции конечного потребления;