
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование надстройки «Поиск решения»Содержание книги
Поиск на нашем сайте
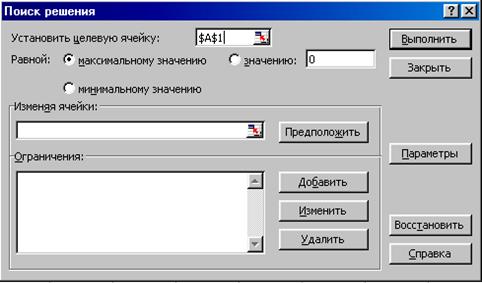
С помощью надстройки Поиск решения можно решать линейные задачи. Надстройка Поиск решения запускается командой Сервис | Поиск решения. Если в меню Сервис отсутствует команда Поиск решения, следует воспользоваться командой Сервис | Надстройки и установить флажок Поиск решения. Вид диалогового окна Поиск решения приведен на рис. 5.1, а опции его настройки – в табл. 5.2.
Таблица 5.2 Опции окна «Поиск решения»
Рис. 5.1. Окно Поиск решения
При нажатии кнопки Параметры в окне Поиск решения открывается окно Параметры поиска решения (рис. 5.2), описание опций которого приведено в табл. 5.3.
Рис. 5.2. Окно Параметры поиска решения
Таблица 5.3 Опции окна «Параметры поиска решения»
Сохранение (загрузка) различных данных для поиска решения осуществляется соответственно с помощью кнопок Сохранить модель и Загрузить модель окна Параметры поиска решения.
При решении задачи с помощью надстройки Поиск решения прежде всего необходимо подготовить рабочий лист MS Excel – корректно разместить на нем все исходные данные, грамотно ввести необходимые формулы для целевой функции и для других зависимостей выбрать место для значений переменных. Рассмотрим задачу. В цехе площадью 74 м2 необходимо установить станки, на приобретение которых отпущено 420 тыс. руб. Существует два типа станков. Станок первого типа стоимостью 60 тыс. руб., требующий 12 м2 производственных площадей, обеспечивает изготовление 70 изделий в смену. Аналогичные характеристики станка второго типа составляют соответственно 40 тыс. руб., 6 м2, 40 изделий в смену. Найти оптимальный вариант приобретения станков, обеспечивающий максимальное производство изделий в цехе. Обозначим Х1 количество станков первого типа, а Х2 – количество станков второго типа, которые предполагается установить в цехе. Тогда количество изделий, которое будет произведено на этих станках равно F(X1, X2)=70*X1+40*X2. Это и есть целевая функция, которую нужно максимизировать. Теперь запишем ограничения. Их в задаче два. Ограничения по финансам: 60*X1+40*X2 £ 420 тыс. руб. Ограничения по площади размещения: 12*X1+6*X2 £ 74 м2. Кроме этих ограничений следует добавить очевидные ограничения: - переменные задачи должны быть неотрицательные X1 ³ 0; X2 ³ 0; - переменные задачи должны быть целочисленные X1, X2 Î Z. Итак, математическая модель сформулирована.
Решение оптимизационных задач в Excel проводится с помощью специализированной программы Поиск решения, вызываемой из главного меню: Сервис | Поиск решения. Она находится в файле SOLVER.XLA, который подключается при первом обращении к этой программе. Эту программу мы уже использовали при нахождении корней нелинейного уравнения. Таким образом, теперь задача состоит в том, чтобы перенести математическую модель в Excel. Порядок действий следующий. 1. Отводим ячейки для каждой независимой переменной задачи. В нашем примере это ячейка B4 для Х1 и ячейка B5 для Х2 (рис. 5.3). Их можно оставить пустыми.
2. Отводим ячейку (С13) для целевой функции и набираем в ней соответствующую формулу: = B4*E4+B5*E5. В формуле в качестве переменных фигурируют адреса ячеек, где расположены соответствующие переменные. Константы задачи заданы не числами, а также ссылками на ячейки, в которых их необходимо предварительно разместить. Рекомендуется для этого оформить таблицу, например, так, как это показано на рис. 5.1. 3. Отводим ячейки (А13 и В13) для создания формул, соответствующих левой части каждого ограничения: =В4*С4+В5*С5 =В4*D4+B5*D5. 4. Открываем диалоговое окно Поиск решения (рис. 5.4). 5. В поле Установить целевую ячейку указываем адрес ячейки, в которой находится формула для расчета целевой функции (ячейка С13). Ниже указываем тип оптимизации (поиск максимума или минимума). 6. В поле Изменяя ячейки отмечаем адреса ячеек, где находятся независимые переменные задачи (В4 и В5).
Рис.5.3.Рабочий лист с результатом решения задачи оптимизации
Рис.5.4. Диалоговое окно Поиск решения с заданными ограничениями и адресами ячеек
7. Для того чтобы ввести ограничения, нужно нажать на кнопку Добавить. Появляется диалоговое окно Добавление ограничения (рис. 5.5).
Рис.5.5. Диалоговое окно Добавление ограничения
В левое поле вводим адрес ячейки, где находятся ограничения (или диапазон адресов ячеек), в центральном поле выбираем знак операции отношения (а также задаем целочисленность или бинарность переменных), в правом поле задаем адрес ячейки (или диапазон адресов), где находятся правые части ограничений. Вместо адресов в правой части можно просто задать числовые значения. Нажатием клавиши Добавить переходим в режим добавления следующего ограничения, нажатием клавиши ОК заканчиваем ввод ограничений. Теперь, если необходимо, в поле Ограничения окна Поиск решения можно выбирать какие-либо ограничения и редактировать их или удалять. 8. Запускаем процесс вычислений нажатием кнопки Выполнить. Результат приведен на рис. 5.3. Заданным ограничениям удовлетворяет следующий парк станков: 3 – первого типа, 6 – второго типа; при этом будет изготовлено максимальное количество деталей – 450. В окне Результаты поиска решения пользователю предлагается составить отчеты, полученные по результатам оптимального решения. Они будут располагаться на отдельных листах данной рабочей книги. С помощью этих отчетов можно получить информацию о степени дефицитности тех или иных ресурсов. Эти вопросы в данной лабораторной работе не рассматриваются, тем более, что для рассматриваемой целочисленной задачи отчет по результатам, например, не дает какой-либо дополнительной информации, а два других отчета закрыты. В окне Поиск решения с помощью кнопки Параметры можно вызвать диалоговое окно Параметры поиска решения (рис. 5.6). Рассмотрим элементы этого окна.
Рис.5.6. Диалоговое окно Параметры поиска решения
Поля Максимальное время и Предельное число итераций определяют время, отпущенное на поиск решения задачи, и число промежуточных вычислений, соответственно. Поля Относительная погрешность, Допустимое отклонение и Сходимость служат для задания точности, с которой ищется решение (последнее используется только для нелинейных моделей). Рекомендуется после решения задачи повторить его с большей точностью (особенно для целочисленных моделей), чтобы проверить точность модели.
Флажок Линейная модель устанавливается для линейных задач и снимается для нелинейных. Флажок Неотрицательные значения позволяет установить нулевую нижнюю границу для тех ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение. Флажок Автоматическое масштабирование служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине, например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей. Флажок Показывать результаты итераций служит для пошагового проведения итераций с целью просмотра промежуточных результатов. Опция Оценки служит для указания метода экстраполяции, используемого при поиске решения. Опция Разности служит для указания метода численного дифференцирования, который используется для вычисления производных при поиске решения. Опция Метод поиска служит для выбора алгоритма оптимизации (метод Ньютона или сопряженных градиентов) для указания направления поиска. Более подробную информацию можно получить, нажав кнопку Справка в том же диалоговом окне. Технология решения транспортной задачи линейного Целью транспортной задачи является планирование наиболее рациональных путей и способов транспортировки товаров. В сущности, технология решения транспортной задачи линейного программирования практически ничем не отличается от технологии решения других оптимизационных задач. Рассмотрим это на примере. Пример 5. 1. На складах Al, A2, A3 имеются запасы товаров в количествах 90, 400 и 110 т соответственно. Грузополучатели Bl, B2, B3должны получить эти товары в количествах 130, 300, 160 т соответственно. Требуется найти такой вариант перевозки грузов, при котором сумма затрат на перевозки будет минимальной. Расходы по перевозке 1 т грузов в условных единицах приведены в таблице 5.4. Таблица 5.4
Решение Математическая модель Введем следующие обозначения: Х11 – количество товара, перевозимое грузополучателю В1 со склада А1; Х12 – количество товара, перевозимое грузополучателю В1 со склада А2; Х13 – количество товара, перевозимое грузополучателю В1 со склада А3; Х21 – количество товара, перевозимое грузополучателю В2 со склада А1; Х22 – количество товара, перевозимое грузополучателю В2 со склада А2; Х23 – количество товара, перевозимое грузополучателю В2 со склада А3;
Х31 – количество товара, перевозимое грузополучателю В3 со склада А1; Х32 – количество товара, перевозимое грузополучателю В3 со склада А1; Х33 – количество товара, перевозимое грузополучателю В3 со склада А3; Тогда целевая функция будет иметь вид L=2x11+5x12+2x13+4x21+x22+5x23+3x31+6x32+8x33 при ограничениях:
В диалоговом окне Поиск решения в соответствующих полях установим адрес целевой ячейки, адрес диапазона, содержащего подбираем параметры, введем все ограничения, установим переключатель Минимальному значению (рис. 5.7). После выполнения вычислений будет получен результат, представленный на рис. 5.8. Минимальные затраты на перевозку грузов со складов потребления при полученном плане перевозок составляет 1360 у.е.
Рис. 5.6
Рис. 5.7
Рис. 5.8
Задания для практической работы Задание 5.1. Пусть уже построена математическая модель некоторой оптимизационной задачи. Найти оптимальное значение целевой функции R(x) при заданных ограничениях с помощью сервисной программы Excel Поиск решения.
1. R(x)= 626x1+ 656x2 ® mах при ограничениях 5x1 + 8x2 £ 81; 6x1 + 4x2 £ 70; 3x1 + x2 £ 26; x1 + x2 £ 12; x1 £ 8; x1, x2 ³ 0.
2. R(x)=–5x1 + 4x2–x3–3x4–5x5 ® min при ограничениях 3x1–x2 + 2x4 + x5 = 5; 2x1–3x2 + x3 + 2x4 + x5 = 6; 3x1–x2 +x3 +3x4 + 2x5 = 9; xi ³ 0, i=1...5.
3. R(x)=–2x1 +x2 + 4x3–x4–x5 ® min при ограничениях x2 + 2x4–x5 =1; x1–x4–x5 =1; 2x2+x3 + 2x5 = 4; xi ³ 0, i=1...5.
4. R(x)= 2x1 + x2 + x3 + 7x4–2x5 ® min при ограничениях x1 +x2–x3 + x4 = 1; 2x1 + x2 + x3 –x5 = 7; x1 + 2x2 + x3 –7x4 + x5 = 6; xi ³ 0, i=1...5.
5. R(x)=–x1 + x2 + x3 + x4 + 3x5 ® min при ограничениях 2x 1 + 2x2+ x4 + x5 =3; 3x1 –x2 + 2x3 – 2x5 =1; –3x1 + 2x3 – x4 + 2x5 = 1; xi ³ 0, i=1...5.
6. R(x)= –4x1 +2x2 –x3 +x4 ® min при ограничениях 3x1 + 2x2 – x3 + 4x4 = 3; x1 – x2 + 4x3 – 2x4 = 2; xi ³ 0, i=1...4.
7. R(x)= x1 + 2x2 + x3 –x4 ® min при ограничениях 10x2 + x3 + 2x4 + 3x5 = 25; –x1 + 5x2 + x3 + x4 + x5 = 10; 2x1 – x2 + x3 – 3x4 = 6; xi ³ 0, i=1...5.
8. R(x)= 4x1 –3x2 – x4 + x5 ® min при ограничениях –x1 + 3x2 + x4 = 13; 4x1 + x2 + x5 = 2; –2x1 + x2 + x3 = 1; x1 – 3x2 + x6 = 0; xi ³ 0, i=1...6.
9. R(x)= x1 – x2 ® mах при ограничениях 2x1 – 4x2 – x3 + x4 = –3; 4x1 – 3x2 – x3 + x4 + x5 = 6; x1 + 4x2 + x3 + x5 = 15; xi ³ 0, i=1...5.
10. R(x)= x1 + 9x2 + 5x3 + 3x4 + 4x5 + 14x6 ® min при ограничениях x1 + x4 = 20; x2 + x5 = 50; x3 + x6 =30; x4 + x5 +x6 = 60; xi ³ 0, i=1...6.
11. R(x)= x1 + x2 ® mах при ограничениях x1 + x2 ³ 1; x1 – x2 ³ –1; x1 – x2 £ 1; x1 £ 2; x2 £ 2; xi ³ 0, i=1...2.
12. R(x)= 4x1 + 6x2 ® min при ограничениях x1 + x2 £ 20; x1 + 3x2 ³ 30; 8x1 + 6x2 ³ 72; 8x1 + 6x2 £ 128; xi ³ 0, i=1...2.
13. R(x)= 3x1 + 8x2 ® mах при ограничениях x1 + 7x2 £ 57; 2x1 + 5x2 £ 42; 3x1 + 4x2 £ 56; 2x1 + x2 £ 34; xi ³ 0, i=1...2.
14. R(x)= x12 + x22 – 10x1 – 15x2 ® min при ограничениях 2x1 + 3x2 £ 13; 2x1 + x2 £ 10; xi ³ 0, i=1...2.
15. R(x)= 3x12 + x22 + 3x1 – 2x2 ® min при ограничениях x1 + 3x2 + x3 + x4 = 16; 3x1 – x2 – x3 + x4 = 4; xi ³ 0, i=1...4.
16. R(x)= x12 + x22 + x32 +x2 – 2x3 ® min при ограничениях x1 + x2 + 2x3 £ 6; 3x1 + 2x2 +x3 £ 12; xi ³ 0, i=1...3.
17. R(x)= –2x1 + 2x2 – 3x3 + 3x4 ® min при ограничениях x1 – 2x2 + x4 = 3; x2 + x3 – 2x4 = 5; 3x2 +x4 + x5 = 6; xi ³ 0, xi Î Z; i=1...5.
18. R(x)= x1 –x2 + x3 – x4 ® mах при ограничениях x1 + 2x3 + x4 = 8; x1 +x2 – x4 = 4; –x1 + 2x2 + x3 + 3x4 = 6; xi ³ 0, xi Î Z; i=1...4.
19. R(x)= x1 + 2x2 + x5 ® min при ограничениях
x1 + x2 + x3 +x4 + x5 = 5; x2 + x3 + x4 – x5 = 2; x3 – x4 + x5 = 1; xi ³ 0, xi Î Z; i=1...5.
20. R(x)= 4x1 + 3x2 ® mах при ограничениях 2x1 + 3x2 +x3 = 8; 4x1 + x2 + x4 = 10; xi ³ 0, xi Î Z; i=1...4.
21. R(x)= – x3 ® min при ограничениях –6x2 + 5x3 +x5 = 6; 7x2 – 4x3 + x4 = 4; x1 + x2 +x3 = 9; xi ³ 0, xi Î Z; i=1...5.
22. R(x)= 3x1 + 2x2 + x3 ® min при ограничениях x1 + 3x2 +x3 ³ 10; 2x1 + 4x3 ³ 14; 2x2 + x3 ³ 7; xi ³ 0, xi Î Z; i=1...3.
23. R(x)= –2x1 – x2 – x3 ® min при ограничениях x1 + 2x2 + 2x3 = 16; x1 + x2 £ 7; 3x1 + 2x2 ³ 18; xi ³ 0, xi Î Z; i=1...3.
24. R(x)= –4x1 – 3x2 ® min при ограничениях 4x1 + x2 £ 44; x1 £ 22; x2 £ 18; xi ³ 0, xi Î Z; i=1...2.
25. R(x)= –6x1 + 2x12 – 2x1x2 + 2x22 ® min при ограничениях x1 + x2 £ 2; x1 + 3x2 £ 3; xi ³ 0, i=1...2.
26. R(x)= x1 + x2 ® mах при ограничениях 0£ х1 + х2 £ 3; –1£ х1 – х2 £ 0; 0£ х1 £ 1; 0£ х2 £ 3; х1 , х2 ³ 0.
27. R(x)= 2x1 + x2 ® mах при ограничениях х1 + 2х2 £ –1; 2х1 + х2 £ 2; х1 – х2 £ –1; –2х1 – 2х2 £ 3; 3х1 + 3х2 £ –2; х1 , х2 ³ 0.
28. R(x)= x1 – x2 ® mах при ограничениях 1£ х1 + х2 £ 2; 2£ х1 – 2х2 £ 3; 1£ 2х1 – х2 £ 2; х1 , х2 ³ 0.
29. R(x)= –9x1 – 2x2 ® mах при ограничениях –х1 – х2 £ 0; –х1 + х2 £ 0; –3х1 – х2 £ 0; –4х1 + х2 £ –1; х1 , х2 ³ 0.
30. R(x)= 2x1 + 3x2 ® min при ограничениях х1 + х2 £ 4; 3х1 + х2 ³ 4; х1 + 5х2 ³ 4; х1 £ 3; х2 £ 3; х1 , х2 ³ 0.
Задание 5.2. Сформулировать математическую модель предложенной задачи оптимизации (целевая функция, система ограничений). С использованием сервисной программы Excel Поиск решения найти оптимальное значение целевой функции. Результаты решения оформить в виде наглядных таблиц.
Задание 5.3. В1. Для изготовления сплава из меди, олова и цинка в качестве сырья используют два сплава тех же металлов, отличающиеся составом и стоимостью. Данные об этих сплавах приведены в таблице.
Получаемый сплав должен содержать не более 2 кг меди, не менее 3 кг олова, а содержание цинка может составлять от 7,2 до 12, 8 кг. Обеспечить количества Xj, j=1,2 сплавов каждого вида, обеспечивающие получение нового сплава с минимальными затратами на сырье.
В2. Для изготовления двух видов изделий А1 и А2 завод использует в качестве сырья алюминий и медь. На изготовлении изделий заняты токарные и фрезерные станки. Исходные данные задачи приведены в таблице.
Определить количества Xj,j=1,2 изделий Аj, которые необходимо изготовить для достижения максимальной прибыли.
В3. Из одного города в другой ежедневно отправляются пассажирские и скорые поезда. В таблице указано количество вагонов в поездах различного типа и максимальное число пассажиров, на которое рассчитан вагон.
Определить число скорых Х1 и пассажирских Х2 поездов, которые необходимо формировать ежедневно из имеющегося парка вагонов, чтобы число перевозимых пассажиров было максимальным. В4. В начале рабочего дня автобусного парка на линию выходит Х1 автобусов, через час к ним добавляется Х2 автобусов, еще через час – дополнительно Х3 машин. Каждый автобус работает на маршруте непрерывно в течение 8 часов. Минимально необходимое число машин на линии в i-й час рабочего дня (i =1,2,...,10) равно bi. Превышение этого числа приводит к дополнительным издержкам в течение i-го часа в размере сi рублей на каждый дополнительный автобус. Определить количества машин Х1 , Х2, Х3, выходящих на маршрут в первые часы рабочего дня, с таким расчетом, чтобы дополнительные издержки в течение всего рабочего дня были минимальными. Исходные данные приведены в таблице.
В5. На товарных станциях С1 и С2 имеется по 30 комплектов мебели. Известно, что перевозка одного комплекта со станции С1 в магазины М1, М2, М3 стоит соответственно 10 руб., 30 руб., 50 руб., а стоимость перевозки со станции С2 в те же магазины - 20 руб., 50 руб., 40 руб. Необходимо доставить в каждый магазин по 20 комплектов мебели. Составить план перевозок так, чтобы затраты на транспортировку мебели были наименьшими.
В6. Предприятие, располагающее ресурсами сырья трех видов Bi, i=1,2,3, может производить продукцию четырех видов Aj, j=1,2,3,4. В таблице указаны затраты ресурсов Bi на изготовление 1 т продукции Aj, объем ресурсов и прибыль, получаемая от изготовления 1 т продукции Aj.
Определить ассортимент выпускаемой продукции, при котором полученная прибыль будет максимальной, при условии: а) продукции А2 необходимо выпустить не менее 8 т, продукции А4 - не более 5 т, а продукции А1 и А3 - в отношении 2:1; б) производственные издержки на 1 т продукции Аj, j=1...4, составляют соответственно 30, 90,120 и 60 руб., а суммарные издержки не должны превышать 960 руб.
В7. Пусть вашей фирме необходимо заключить контракт на поставку товаров на некоторую сумму, меньшую или равную Р условных единиц. При этом имеется выбор из N партнеров, которые могут поставить товар на Ki условных единиц каждый. Ожидаемая прибыль от сделки с i-м партнером составляет Ci процентов от суммы заключенной сделки, но при этом риск от сделки с i-м партнером составляет Hi процентов от суммы сделки. Требуется определить наиболее выгодных партнеров и сумму сделки с каждым из них, обеспечив при этом максимальное значение прибыли при значении суммарного риска от сделок, не превышающего суммы прибыли. Исходные данные приведены в таблице.
В8. Ваше предприятие выпускает телевизоры, музыкальные центры и акустические системы, используя общий склад комплектующих. В связи с ограниченностью запаса необходимо найти оптимальное соотношение объемов выпуска изделий. Цель – получение максимальной прибыли. Для обеспечения договоров с заказчиками необходимо выпускать не менее 100 единиц каждого наименования. Следует учитывать уменьшение удельной прибыли при увеличении объемов производства (в связи с дополнительными затратами на сбыт) по степенному закону (коэффициент отдачи к=0,9). Данные для расчета приведены в таблице.
В9. Для работников с пятидневной рабочей неделей и двумя выходными подряд требуется составить график работы, обеспечивающий требуемый уровень обслуживания при наименьших затратах на оплату труда. Дневная оплата каждого работника – 40 руб.
Указание. Разбить всех работников на 7 групп и обозначить Х1 - количество работников, отдыхающих в воскресенье-понедельник, Х2 - количество работников, отдыхающих в понедельник-вторник, и т.д.
В10. Требуется минимизировать затраты на перевозку товаров от предприятий-производителей на торговые склады. При этом необходимо учесть возможности поставок каждого из производителей при максимальном удовлетворении запросов потребителей. Данные для расчета приведены в таблице. Сколько необходимо сделать рейсов, если за один рейс можно перевезти 20 т груза.
В11. Маркетологи фирмы установили, что между расходами на рекламу R (руб.) и числом продаж N (шт.) существует связь, выражаемая формулой N=35d(R+3000)0,5, где коэффициент d - сезонная поправка. Определить бюджет на рекламу в каждом квартале, соответствующий наибольшей прибыли за год, при фиксированных затратах на торговый персонал. Оценить поквартально норму прибыли (отношение производственной прибыли к выручке от реализации). Годовые затраты на рекламу не должны превышать 40000 руб. Цена одного изделия - 40 руб., затраты на сбыт одного изделия - 25 руб.
В12. Фабрика выпускает кожаные брюки, куртки и пальто специального назначения в ассортименте, заданном отношением 2:1:3. В процессе изготовления изделия проходят три производственных участка - дубильный, раскройный и пошивочный. Данные для расчета приведены в таблице.
Ограничения на фонд времени для участков составляют, соответственно, 3360, 2688, 5040 чел.×ч. Учитывая заданный ассортимент, максимизировать прибыль от реализованной продукции.
В13. На заводе ежемесячно скапливается около 14 т отходов металла, из которого можно штамповать большие и малые шайбы. Месячная потребность завода в больших шайбах 600 тыс. шт., в малых - 1100 тыс. шт. Расход металла на тысячу больших шайб - 22 кг, на тысячу малых - 8 кг. Для изготовления шайб используются два пресса холодной штамповки. Производительность каждого за смену 9 тыс. шт. больших шайб либо 11,5 тыс. шт. малых. Завод работает в две смены. Недостающее количество шайб закупается. Оптовая цена больших шайб 11,9 руб. (за тысячу штук), а малых - 5,2 руб. Определить месячный план производства шайб, обеспечивающий максимальную долю в валовой продукции предприятия.
В14. Цех мебельного комбината выпускает трельяжи, трюмо и тумбочки под телевизор. Исходя из необходимости выполнения плана по ассортименту и возможности его перевыполнения по отдельным (или по всем) показателям, построить модели, на основе которых можно сформулировать следующие экстремальные задачи: 1) задачу максимизации объема реализации (за плановый период); 2) задачу максимизации прибыли (за тот же период). Данные для расчета приведены в таблице. Определить недостающие данные и задать их самостоятельно.
В15. Предприятие выпускает обычный, специальный и декоративный сплавы латуни и реализует их, соответственно, по 3; 4,5 и 6 руб. за единицу веса. Его производственные мощности позволяют производить (за плановый период) не более 500 ед. веса обычного сплава, 700 ед. - специального и 250 ед. - декоративного. Обязательными составляющими сплавов являются медь, цинк, свинец и никель. Их цена соответственно 0,9; 0,7; 0,5 и 1,1 руб. за единицу веса. По технологии декоративный сплав должен содержать не менее 7% никеля, 49% меди и не более 29% свинца; специальный - не менее 3% никеля, 71% меди, 9% цинка и не более 21% свинца. В обычный сплав составляющие входят без ограничений. Считая, что себестоимость сплавов складывается только из стоимости его ингредиентов, составить план выпуска сплавов, обеспечивающий максимальную прибыль. В16. Рацион стада крупного рогатого скота из 220 голов включает пищевые продукты A, B, C, D и E. В сутки одно животное должно съедать не менее 2 кг продукта вида А, 1,5 кг продукта В, 0,9 кг продукта С, 3 кг продукта D и 1,8 кг продукта Е. Однако в чистом виде указанные продукты не производятся. Они содержатся в концентратах К-1, К-2, К-3. Их цена и содержание продуктов (в процентах) приведены в таблице.
Минимизировать затраты на покупку концентратов при рациональном кормлении скота.
В17. Нефтеперерабатывающий завод получает за плановый период четыре полуфабриката – 600 тыс. л алкилата, 316 тыс. л крекинг-бензина, 460 тыс. л бензина прямой перегонки и 200 тыс. л изопентана. В результате смешивания этих ингредиентов в пропорциях 2:3:1:5, 2:4:3:4:, 5:1:6:2 и 7:1:3:2 получают бензин четырех сортов Б-1, Б-2, Б-3, Б-4. Цена его реализации, соответственно, 2руб.; 2 руб.10 коп.; 2 руб.60 коп.; 2 руб.30 коп. за литр. 1. Спланировать ассортимент выпускаемой продукции, обеспечивающий максимальную прибыль. 2. Решить задачу, введя ограничение снизу на ассортимент продукции.
В18. Для поддержания нормальной жизнедеятельности человеку ежедневно необходимо потреблять не менее 118 г белков, 56 г жиров, 500 г углеводов, 8 г минеральных солей. Количество
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1074; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.85.61 (0.015 с.) |






 min
min Представим математическую модель на рабочем листе в виде, изображенном на рис. 5.6, записывая в ячейку В9 формулу функции цели, а в ячейки В11 - В16 формулы ограничений.
Представим математическую модель на рабочем листе в виде, изображенном на рис. 5.6, записывая в ячейку В9 формулу функции цели, а в ячейки В11 - В16 формулы ограничений.





