Технологии финансовых вычислений

Цель работы: научиться технологии решения финансовых задач

 

Теоретическое введение

Расчет наращенной суммы

Под наращенной суммой ссуды (депозита, долга) понимается ее первоначальная сумма плюс начисленные на нее к концу срока проценты. Наращенная сумма вычисляется как последний элемент прогрессии, имеющей общий член,

Р(1+ni), т.е. S=P(1+ni),

где Р - первоначальная сумма;

п - количество периодов;

i - ставка за период.

 

Вычисление количества дней в периоде, заданном начальной и конечной датами

При продолжительности ссуды, не кратной году, необходимо определить, какая часть процента выплачивается кредитору. В табличном процессоре для вычисления количества дней между двумя датами служит функция

ДНЕЙ360 (Нач_дата; Кон_дата; Метод).

Параметр Метод определяет метод расчета: 1 - дата выдачи и дата погашения считается как один день (Европейский); 0 - дата выдачи и дата погашения считается как разные дни (Американский).

Вычисления по простым переменным ставкам

В течение расчетного периода процентные ставки могут дискретно изменяться во времени, при этом они остаются постоянными до следующего дискретного изменения. В этом случае формула для расчета наращенной суммы имеет вид

, где

i_t - ставка простых процентов в периоде с номером t = 1... т;

n_t - продолжительность t периода начисления по ставке i_t.

Пример 3.1 В договоре, рассчитанном на год, принята ставка простых процентов на I квартал в размере 8% годовых, а на каждый после­дующий квартал - на 0,5% меньше, чем в предыдущем. Определить сумму на счете в конце года.

Решение

Применим приведенную выше формулу и реализуем ее на рабочем листе в виде модели, приведенной на рис. 3.1.

Рис. 3.1

 

Вычисление накопленной суммы при реинвестировании по простым процентам

Сумма с начисленными на нее процентами может быть вновь инвестирована под эту или другую процентную ставку. В случае многократного периодического реинвестирования с применением простой процентной ставки наращенная сумма для всего срока N=Σni вычисляется по формуле

,

где п_t - продолжительности последовательности периодов реинвестирования;

i_t - ставки, по которым производится реинвестирование.

В табличном процессоре приведенную формулу реализует финансовая функция БС. Эта функция также учитывает равномерные периодические выплаты (если они производятся), которые выполняются в те же периоды, что и реинвестирование.

Пример 3.2 На сумму 100 тыс. ден. ед. начисляется 10% годовых. Проценты простые, точные. Вычислить сумму наращения к концу квартала, если в течение квартала ежемесячно производится реинвестирование.

Решение

Применим приведенную выше формулу и реализуем ее на рабочем листе в виде модели, приведенной на рис. 3.2

Рис. 3.2

 

Результат решения приведен на рис. 3.3.

Рис. 3.3

 

Решение этой задачи с использованием функции БС приведено на рис. 3.4.

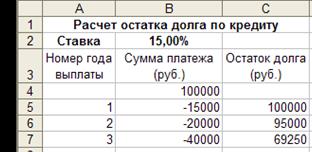
Рис. 3.4

Пример 3.3 Клиент в начале года получил кредит по годовой ставке 15% (проценты простые) в размере 100 000 руб. Погашение кредита выполнялось неравномерными платежами в конце каждого года в течение 3 лет: 15 000 руб., 20 000 руб., 40 000 руб.

Требуется вычислить остаток долга в конце третьего года.

Решение

В предположении, что начисление по процентам выполняется в конце года без учета текущего платежа, разработаем в табличном процессоре модель вычислений (рис. 3.5).

Рис. 3.5

 

Результат вычисления приведен на рис. 3.6.

Рис. 3.6

 

Остаток долга по кредиту составляет 69250 руб.

Дисконтирование по простым процентам

Операция дисконтирования заключается в вычислении исходной суммы Р, при заданной сумме S, соответствующей концу финансовой операции. Начисления по процентам в виде разности D = S - Р называют дисконтом (скидкой).

Дисконтная сумма по простой ставке вычисляется по формуле

Р= S/(1 +ni).

В табличном процессоре для вычисления дисконтной суммы предназначена функция ПС.

 

Пример 3.4 Определить сумму вклада, которую нужно положить в банк сроком на два месяца под 10% годовых, чтобы к концу срока получить 101 667 руб. Расчеты выполнить для случая простых процентов.

Решение

Решение и полученный результат приведен на рис. 3.7.

Рис. 3.7

Решение этой задачи с использованием функции ПС приведено на рис. 3.8

Рис. 3.8

Пример 3.5 Платежное обязательство уплатить через 60 дней 200 000 руб. с процентами, начисляемыми по ставке простых процентов i = 15% годовых, было учтено за 10 дней до срока погашения по учетной ставке 10%. Вычислить сумму, получаемую при учете (число дней в году 365).

Решение

Используем приведенную выше формулу и реализуем ее на рабочем листе в виде модели, приведенной на рис. 3.9.

Рис. 3.9

Результат решения приведен на рис. 3.10.

Рис. 3.10