Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности машинной арифметики, точность вычислений на эвмСодержание книги
Поиск на нашем сайте ВВЕДЕНИЕ Цикл лабораторных работ предназначен для студентов второго курса (четвертый семестр), изучающих дисциплину "Вычислительная математика" и работающих в компьютерных классах на базе ЭВМ типа IBM PC AT-286 и выше, снабженных компилятором языка С (С++). Первые две работы цикла посвящены особенностям машинной арифметики, точности вычислений на ЭВМ и обусловленности вычислительной задачи. Они служат практической иллюстрацией вводной части теоретического курса дисциплины. Каждая из последующих работ ставит целью изучение либо конкретного численного метода, либо набора численных процедур (схем, формул), позволяющих реализовать выполнение одной из классических задач вычислительной математики: решение нелинейных уравнений, интерполирование функций, численное интегрирование, решение систем линейных алгебраических уравнений. Порядок расположения лабораторных работ в методических указаниях соответствует последовательности изложения лекционного материала. Для углубленного изучения перечисленных выше задач и методов их решения целесообразно воспользоваться литературой [1-10], приведенной в библиографическом списке. Выполнение каждой лабораторной работы следует осуществлять поэтапно в следующем порядке: - подготовка к решению задачи на персональной ЭВМ (ПЭВМ); - проведение вычислительного эксперимента на ПЭВМ; - анализ результатов вычислений; оформление отчета. Подготовка к решению задачи на ПЭВМ производится как вне компьютерного класса, так и непосредственно на ПЭВМ. Она включает: - ознакомление с описанием работы и заданием для выполнения; - составление программных модулей, содержащих определенные заданием и персональным вариантом вычислительной процедуры, и/или ввод исходных данных; - компиляцию разработанных программных модулей, их отладку и сопряжение с имеющимся для большинства работ программами-функциями, реализующими конкретные численные методы; - планирование вычислительного эксперимента на ПЭВМ в рамках выполняемого задания. Программы - функции, предназначенные для применения в процессе вычислений, представлены в виде библиотеки модулей на языке программирования С++. Это предопределяет ориентацию цикла работ на студентов, владеющих данным языком и навыками программирования в необходимом объеме. Проведение вычислительного эксперимента на ПЭВМ осуществляется в соответствии с порядком выполнения работы и заданием на исследование указанных зависимостей и обусловленности изучаемого метода. Анализ результатов вычислений заключается в построении исследуемых зависимостей и сравнительной оценке метода (вычислительной процедуры) по характерным для данной группы методов параметрам, например, скорости сходимости, степени обусловленности, достижимой точности и т.п. Анализ результатов и оформление отчета производится вне компьютерного класса. Отчет должен содержать: - постановку задачи; - тексты разработанных программ; - результаты вычислений, их теоретический и экспериментальный анализ в виде таблиц и графиков, снабженных необходимыми комментариями; - развернутые выводы по лабораторной работе. В методических указаниях приведено также задание на курсовую работу, которая ориентирована на исследование четырех методов решения нелинейных уравнений.
Общие сведения
Пусть задана непрерывная функция В первом случае итерационный процесс заканчивается, как только длина текущего интервала становится достаточно малой (например, ½bn-an½<e). Во втором случае условием остановки вычислений является малость очередного приращения hn=xn-xn-1, ½hn½<e. В обоих случаях параметр e определяет момент остановки вычислений. Иногда в качестве условия остановки используют условие ½ Для каждого итерационного метода можно указать некоторые условия сходимости. Однако не всегда легко проверить или гарантировать выполнение этих условий. Кроме того необходимо учесть особенности машинных вычислений при реализации итерационных методов. На практике эти затруднения обходят, вводя ограничение nmax на число итераций. Такое ограничение предохраняет от "зацикливания" метода, а также позволяет выявить практическое отсутствие сходимости вычислительного процесса. Целью лабораторных работ, приводимых в данном разделе, является изучение перечисленных выше четырех итерационных методов приближенного решения нелинейных уравнений, при этом каждая работа посвящена одному из них. Для выполнения работ предлагается использовать набор программ - функций, реализующих конкретные численные методы, а также программу - функцию Round, позволяющую моделировать ошибки в исходных данных. Указанные программы (язык C) размещаются в директории LIBR1.
Метод бисекции (Лабораторная работа №3)
Если найден отрезок [a,b], такой, что Рассмотрим один шаг итерационного процесса. Пусть на (n-1)-м шаге найден отрезок [an-1, bn-1]Ì[a, b], такой, что an=an-1, bn=x, если an=x, bn= bn-1, если Если требуется найти корень с точностью e, то деление пополам продолжается до тех пор, пока длина отрезка не станет меньше 2e. Тогда координата середины отрезка есть значение корня с требуемой точностью e. Метод бисекции является простым и надежным методом поиска простого корня уравнения В лабораторной работе №3 предлагается, используя программы - функции BISECT и Round из файла methods.cpp (файл заголовков metods.h, директория LIBR1), найти корень уравнения Выполнение работы осуществляется по индивидуальным вариантам заданий (нелинейных уравнений), приведенным в подразделе 3.6. Номер варианта для каждого студента определяется преподавателем. Порядок выполнения работы должен быть следующим: 1) Графически или аналитически отделить корень уравнения 2) Составить подпрограмму вычисления функции 3) Составить головную программу, содержащую обращение к подпрограмме f(x), BISECT, Round и индикацию результатов. 4) Провести вычисления по программе. Построить график зависимости числа итераций от Eps. 5) Исследовать чувствительность метода к ошибкам в исходных данных. Ошибки в исходных данных моделировать с использованием программы Round, округляющей значения функции с заданной точностью Delta. Текст программы-функции BISECT, предназначенной для решения уравнения
Метод хорд (Лабораторная работа №4)
Пусть найден отрезок [a, b], на котором функция
Сначала находится уравнение хорды АВ:
Для точки пересечения ее с осью абсцисс (x=c0, y=0) получается уравнение
Далее сравниваются знаки величин Алгоритмы методов бисекции и хорд похожи, однако метод хорд в ряде случаев дает более быструю сходимость итерационного процесса, причем успех его применения, как и метода бисекции, гарантирован. В лабораторной работе №4 предлагается, используя программы - функции HORDA и Round из файла methods.cpp (файл заголовков metods.h, директория LIBR1), найти корень уравнения Для данной работы, как и для лабораторной работы №3 задаются индивидуальные варианты нелинейных уравнений (см. подраздел 3.6). Порядок выполнения лабораторной работы №4: 1) Графически или аналитически отделить корень уравнения 2) Составить подпрограмму - функцию вычисления функции 3) Составить головную программу, вычисляющую корень уравнения 4) Провести вычисления по программе. Теоретически и экспериментально исследовать скорость сходимости и обусловленность метода. В подразделе 3.7 приводится текст программы - функции HORDA, предназначенной для решения уравнения Метод Ньютона (Лабораторная работа № 5)
В случае, когда известно хорошее начальное приближение решения уравнения
Метод Ньютона допускает простую геометрическую интерпретацию (рис. 2). Если через точку с координатами Для оценки погрешности n-го приближения корня предлагается пользоваться неравенством
где М2-наибольшее значение модуля второй производной
Рассмотрим один шаг итераций. Если на (n-1)-м шаге очередное приближение xn-1 не удовлетворяет условию окончания процесса, то вычисляются величины В лабораторной работе № 5 предлагается, используя программы-функции NEWTON и ROUND из файла methods.cpp (файл заголовков methods.h, директория LIBR1), найти корень уравнения Для данной работы вид функции Порядок выполнения лабораторной работы №5. 1) Графически или аналитически отделить корень уравнения 2) Составить подпрограммы - функции вычисления 3) Составить головную программу, вычисляющую корень уравнения 4) Выбрать начальное приближение корня x0 из [Left, Right] так, чтобы 5) Провести вычисления по программе. Исследовать скорость сходимости метода и чувствительность метода к ошибкам в исходных данных. Для приближенного вычисления корней уравнения
Метод простых итераций (Лабораторная работа №6)
Метод простых итераций решения уравнения Рассмотрим один шаг итерационного процесса. Исходя из найденного на предыдущем шаге значения xn-1, вычисляется y= j(xn-1). Если Для применения метода простых итераций определяющее значение имеет выбор функции В лабораторной работе № 6 предлагается, используя программы-функции ITER и Round из файла methods.cpp (файл заголовков methods.h, директория LIBR1), найти корень уравнения Для данной работы вид функции Порядок выполнения лабораторной работы №6 должен быть следующим. 1) Графически или аналитически отделить корень уравнения 2) Преобразовать уравнение 3) Выбрать начальное приближение, лежащее на [Left, Right]. 4) Составить подпрограмму для вычисления значений 5) Составить головную программу, вычисляющую корень уравнения и содержащую обращение к программам 6) Провести вычисления по программе. Исследовать скорость сходимости и обусловленность метода. Текст программы - функции ITER, позволяющей вычислять корни уравнения x=
3.6. Курсовая работа по дисциплине и варианты заданий
Лабораторные работы, описанные в настоящем разделе, целесообразно объединять для выполнения курсовой работы, нацеленной на сравнительную оценку различных методов приближенного решения нелинейных уравнений. Типовое задание на курсовую работу формулируется следующим образом. Задание на курсовую работу по дисциплине "Вычислительная математика". Используя программы - функции BISECT, NEWTON, HORDA, ITER, Round из файла methods.cpp (файл заголовков methods.h, директория LIBR1), найти корень уравнения Исследуйте обусловленность методов и зависимость числа итераций от точности результата Eps при изменении Eps от 0.0 до 0.000001. Порядок выполнения курсовой работы Графически или аналитически отделить корень уравнения Составить подпрограмму- функцию вычисления функции Составить головную программу, содержащую ввод исходных данных, обращение к подпрограммам BISECT, NEWTON, HORDA, ITER вывод результатов. Выполнить вычисления по программе. Построить графики зависимости числа итераций, необходимых для достижения заданной точности Eps, от величины Eps, а также достижимой точности результатов от точности Delta задания функции Теоретически и экспериментально сравнить методы бисекции, Ньютона, хорд и итераций по скорости сходимости и степени обусловленности. Результаты оформить в виде отчета, содержащего постановку задачи, тексты разработанных программ, результаты теоретического и экспериментального анализа в виде таблиц и графиков, выводы. Вид функции
Численное интегрирование Библиографический список
1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: Уч.пособие.- М.: Высш.шк., 1994. - 544 с. 2. Бахвалов Н.С., Жидков Н.О., Кобельков Г.М. Численные методы. - М.: Наука, 1987. - 600 с. 3. Березин И.С., Жидков Н.П. Методы вычислений. Т.1.- М.: Наука, 1966. - 632. 4. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 1970. - 664 с. 5. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. - М.: Наука, 1972. - 367 с. 6. Марчук Г.И. Методы вычислительной математики. - М.: Наука, 1989. - 608 с. 7. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математики: Учеб. Пособие для втузов. - 2-е изд. - М.: Высш.шк., 1994. - 416 с. 8. Самарский А.А., Гулин А.В. Численные методы. - М.: Наука, 1989. - 432 с. 9. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений/Пер. с англ. - М.: Мир, 1980. - 279 с. 10. Хемминг Р. Численные методы/Пер. с англ. - М.: Наука, 1972. - 400 с. 11. Сборник задач по структурному программированию: Учеб. пособие/С.А. Ивановский, Ю.Е. Прокофьев, А.В. Смольянинов / Под ред. В.И. Тимохина. - Л.: ЛЭТИ, 1987. - 64 с. 12. Воробьева Г.Н., Данилова А.Н. Практикум по численным методам. - М.: Высш.шк, 1979. - 184 с. 13. Волков Е.А. Численные методы: Учеб. пособие. - М.: Наука, 1982. - 256 с. 14. Основы математического моделирования. Построение и анализ моделей с примерами на языке MATLAB: Учеб. пособие/ Д.Л. Егоренков, А.Л. Фрадков, В.Ю. Харламов; Под ред. А.Л. Фрадкова. - С.-Пб.: БГТУ, 1994. - 192 с. 15. Компьютерная математика. Методич. указ. к лаборат. работам/Сост. И.А. Назаров. - С.-Пб.: ГЭТУ, 1993. - 32 с.
Содержание
ÂÂÅÄÅÍÈÅ................................................................................................................................................................................................... 1. ÎÑÎÁÅÍÍÎÑÒÈ ÌÀØÈÍÍÎÉ ÀÐÈÔÌÅÒÈÊÈ, ÒÎ×ÍÎÑÒÜ ÂÛ×ÈÑËÅÍÈÉ ÍÀ ÝÂÌ............................................................................ (Ëàáîðàòîðíàÿ ðàáîòà ¹1)................................................................................................................................................................ 2. ÈÇÓ×ÅÍÈÅ ÏÎÍßÒÈß ÎÁÓÑËÎÂËÅÍÍÎÑÒÈ ÂÛ×ÈÑËÈÒÅËÜÍÎÉ ÇÀÄÀ×È................................................................................. (Ëàáîðàòîðíàÿ ðàáîòà ¹2)............................................................................................................................................................... 3. ÐÅØÅÍÈÅ ÍÅËÈÍÅÉÍÛÕ ÓÐÀÂÍÅÍÈÉ............................................................................................................................................ 3.1. Îáùèå ñâåäåíèÿ.......................................................................................................................................................................... 3.2. Ìåòîä áèñåêöèè........................................................................................................................................................................... (Ëàáîðàòîðíàÿ ðàáîòà ¹3).............................................................................................................................................................. 3.3. Ìåòîä õîðä....................................................................................................................................................................................... (Ëàáîðàòîðíàÿ ðàáîòà ¹4).............................................................................................................................................................. 3.4. Ìåòîä Íüþòîíà................................................................................................................................................................................. (Ëàáîðàòîðíàÿ ðàáîòà ¹ 5)............................................................................................................................................................. 3.5. Ìåòîä ïðîñòûõ èòåðàöèé....................................................................................................................................................... (Ëàáîðàòîðíàÿ ðàáîòà ¹6).............................................................................................................................................................. 3.6. Êóðñîâàÿ ðàáîòà ïî äèñöèïëèíå è âàðèàíòû çàäàíèé......................................................................................... 3.7. Ïðîãðàììû äëÿ ðåøåíèÿ íåëèíåéíûõ óðàâíåíèé......................................................................................................... 4. ×ÈÑËÅÍÍÎÅ ÈÍÒÅÃÐÈÐÎÂÀÍÈÅ....................................................................................................................................................... 4.1. Ñîñòàâíûå ôîðìóëû ïðÿìîóãîëüíèêîâ, òðàïåöèé, Ñèìïñîíà.................................................................................. (Ëàáîðàòîðíàÿ ðàáîòà ¹6).............................................................................................................................................................. 4.2. Ôîðìóëà Ãàóññà. (Ëàáîðàòîðíàÿ ðàáîòà ¹7)............................................................................................................... Áèáëèîãðàôè÷åñêèé ñïèñîê........................................................................................................................................................
ВВЕДЕНИЕ Цикл лабораторных работ предназначен для студентов второго курса (четвертый семестр), изучающих дисциплину "Вычислительная математика" и работающих в компьютерных классах на базе ЭВМ типа IBM PC AT-286 и выше, снабженных компилятором языка С (С++). Первые две работы цикла посвящены особенностям машинной арифметики, точности вычислений на ЭВМ и обусловленности вычислительной задачи. Они служат практической иллюстрацией вводной части теоретического курса дисциплины. Каждая из последующих работ ставит целью изучение либо конкретного численного метода, либо набора численных процедур (схем
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 497; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

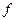 вещественного аргумента x и требуется численным методом решить уравнение
вещественного аргумента x и требуется численным методом решить уравнение 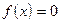 , т.е. найти приближение x* к вещественному корню этого уравнения. Если уравнение имеет несколько вещественных корней, то сначала производят их отделение (изоляцию), а затем уточняют положение отдельного корня. Считается, что отделение корня произведено, если выделен такой интервал [a0, b0] области определения функции
, т.е. найти приближение x* к вещественному корню этого уравнения. Если уравнение имеет несколько вещественных корней, то сначала производят их отделение (изоляцию), а затем уточняют положение отдельного корня. Считается, что отделение корня произведено, если выделен такой интервал [a0, b0] области определения функции 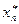 ) ½<e, где
) ½<e, где 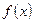 (корень уравнения
(корень уравнения 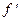 (с)¹0). Этот метод сходится для любых непрерывных функций
(с)¹0). Этот метод сходится для любых непрерывных функций 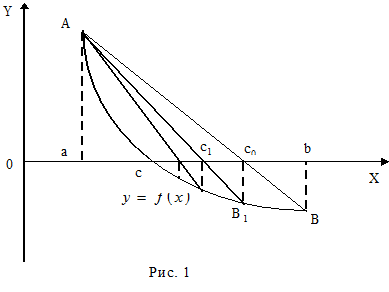
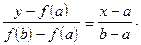
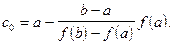
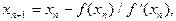 сходящейся к корню уравнения
сходящейся к корню уравнения 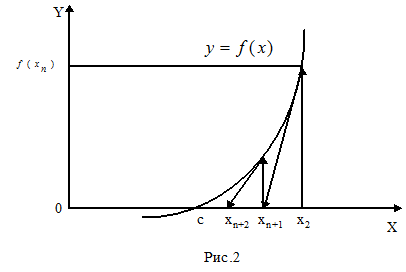
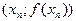 провести касательную, то абсцисса точки пересечения этой касательной с осью Ох будет очередным приближением xn+1 корня уравнения
провести касательную, то абсцисса точки пересечения этой касательной с осью Ох будет очередным приближением xn+1 корня уравнения 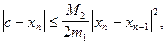
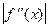 на отрезке [a,b]; m1-наименьшее значение модуля первой производной
на отрезке [a,b]; m1-наименьшее значение модуля первой производной 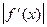 на отрезке [a,b]. Таким образом, если
на отрезке [a,b]. Таким образом, если 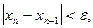 то
то 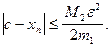 Это означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т.е. процесс сходится очень быстро (имеет место квадратическая сходимость). Из указанного следует, что при необходимости нахождения корня с точностью e итерационный процесс можно прекращать, когда
Это означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т.е. процесс сходится очень быстро (имеет место квадратическая сходимость). Из указанного следует, что при необходимости нахождения корня с точностью e итерационный процесс можно прекращать, когда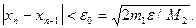 (3.1)
(3.1)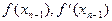 и следующие приближение корня
и следующие приближение корня 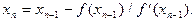 При выполнении условия (3.1) величина xn принимается за приближенное значение корня с, вычисленное с точностью e.
При выполнении условия (3.1) величина xn принимается за приближенное значение корня с, вычисленное с точностью e.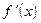 , предусмотрев округление их значений с заданной точностью Delta.
, предусмотрев округление их значений с заданной точностью Delta.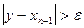 , то полагается xn=y и выполняется очередная итерация. Если же
, то полагается xn=y и выполняется очередная итерация. Если же 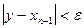 , то вычисления заканчиваются и за приближенное значение корня принимается величина xn=y. Погрешность результата вычислений зависит от знака производной
, то вычисления заканчиваются и за приближенное значение корня принимается величина xn=y. Погрешность результата вычислений зависит от знака производной 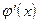 : при
: при 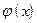 в уравнении
в уравнении 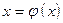 , эквивалентном исходному. Функцию
, эквивалентном исходному. Функцию 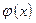 ,
, 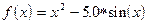 ;
;
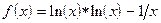
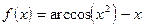 ;
;
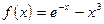 ;
;
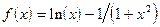 ;
;
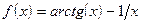 ;
;
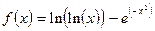 ;
;
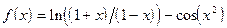 ;
;
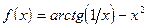 ;
;
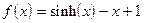 ;
;
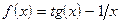 ;
;
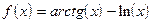 ;
;
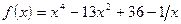 ;
;
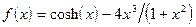 ;
;
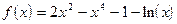 ;
;
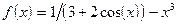 ;
;
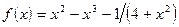 ;
;
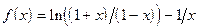 ;
;
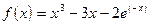 ;
;
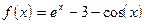 ;
;
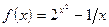 ;
;
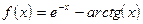 ;
;
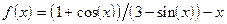 ;
;
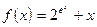 ;
;
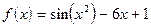 ;
;
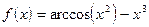 ;
;
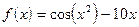 ;
;
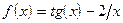 ;
;
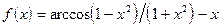 ;
;
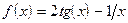 ;
;
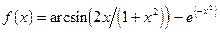 ;
;
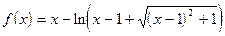 ;
;
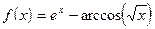 ;
;
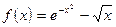 ;
;
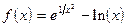 ;
;
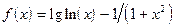 ;
;