Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составные формулы прямоугольников, трапеций, Симпсона.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
(Лабораторная работа №6) Повышения точности численного интегрирования добиваются путем применения составных формул. Для этого при нахождении определенного интеграла отрезок На сетке формула прямоугольников
формула трапеций
формула Симпсона
где Для практической оценки погрешности квадратурной можно использовать правило Рунге. Для этого проводят вычисления на сетках с шагом
За погрешность приближенного значения интеграла для формул прямоугольников и трапеций тогда принимают величину В лабораторной работе №6 требуется, используя квадратурные формулы прямоугольников, трапеций и Симпсона, вычислить значения заданного интеграла и, применив правило Рунге, найти наименьшее значение Порядок выполнения лабораторной работы №6. 1) Составить программы-функции для вычисления интегралов по формулам прямоугольников, трапеций и Симпсона. 2) Составить программу-функцию для вычисления подынтегральной функции. 3) Составить головную программу, содержащую оценку по Рунге погрешности каждой из перечисленных выше квадратурных формул, удваивающих 4) Провести вычисления по программе, добиваясь, чтобы результат удовлетворял требуемой точности. 5) Результаты работы оформить в виде краткого отчета, содержащего сравнительную оценку применяемых для вычисления формул.
Варианты заданий приведены в таблице 4.1 (
Формула Гаусса. (Лабораторная работа №7)
В квадратурной формуле Гаусса
узлы
где Если подынтегральная функция достаточно гладкая, то формула Гаусса обеспечивает очень высокую точность при небольшом числе узлов. В лабораторной работе №7 требуется, используя квадратурную формулу Гаусса наивысшего порядка точности, вычислить приближенное значение заданного интеграла. Интеграл предлагается вычислить по квадратурной формуле Гаусса с восемью узлами:
Порядок выполнения лабораторной работы №7. 1) Составить программу-функцию для вычисления интеграла по формуле Гаусса. 2) Составить программу-функцию для вычисления значений подынтегральной функции. 3) Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов. 4) Результаты работы оформить в виде краткого отчета, содержащего характеристику используемого метода вычислений, его точности и полученное значение интеграла. Варианты заданий к лабораторной работе приведены в таблице 4.2.
Библиографический список
1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: Уч.пособие.- М.: Высш.шк., 1994. - 544 с. 2. Бахвалов Н.С., Жидков Н.О., Кобельков Г.М. Численные методы. - М.: Наука, 1987. - 600 с. 3. Березин И.С., Жидков Н.П. Методы вычислений. Т.1.- М.: Наука, 1966. - 632. 4. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 1970. - 664 с. 5. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. - М.: Наука, 1972. - 367 с. 6. Марчук Г.И. Методы вычислительной математики. - М.: Наука, 1989. - 608 с.
7. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математики: Учеб. Пособие для втузов. - 2-е изд. - М.: Высш.шк., 1994. - 416 с. 8. Самарский А.А., Гулин А.В. Численные методы. - М.: Наука, 1989. - 432 с. 9. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений/Пер. с англ. - М.: Мир, 1980. - 279 с. 10. Хемминг Р. Численные методы/Пер. с англ. - М.: Наука, 1972. - 400 с. 11. Сборник задач по структурному программированию: Учеб. пособие/С.А. Ивановский, Ю.Е. Прокофьев, А.В. Смольянинов / Под ред. В.И. Тимохина. - Л.: ЛЭТИ, 1987. - 64 с. 12. Воробьева Г.Н., Данилова А.Н. Практикум по численным методам. - М.: Высш.шк, 1979. - 184 с. 13. Волков Е.А. Численные методы: Учеб. пособие. - М.: Наука, 1982. - 256 с. 14. Основы математического моделирования. Построение и анализ моделей с примерами на языке MATLAB: Учеб. пособие/ Д.Л. Егоренков, А.Л. Фрадков, В.Ю. Харламов; Под ред. А.Л. Фрадкова. - С.-Пб.: БГТУ, 1994. - 192 с. 15. Компьютерная математика. Методич. указ. к лаборат. работам/Сост. И.А. Назаров. - С.-Пб.: ГЭТУ, 1993. - 32 с.
Содержание
ÂÂÅÄÅÍÈÅ................................................................................................................................................................................................... 1. ÎÑÎÁÅÍÍÎÑÒÈ ÌÀØÈÍÍÎÉ ÀÐÈÔÌÅÒÈÊÈ, ÒÎ×ÍÎÑÒÜ ÂÛ×ÈÑËÅÍÈÉ ÍÀ ÝÂÌ............................................................................ (Ëàáîðàòîðíàÿ ðàáîòà ¹1)................................................................................................................................................................ 2. ÈÇÓ×ÅÍÈÅ ÏÎÍßÒÈß ÎÁÓÑËÎÂËÅÍÍÎÑÒÈ ÂÛ×ÈÑËÈÒÅËÜÍÎÉ ÇÀÄÀ×È................................................................................. (Ëàáîðàòîðíàÿ ðàáîòà ¹2)............................................................................................................................................................... 3. ÐÅØÅÍÈÅ ÍÅËÈÍÅÉÍÛÕ ÓÐÀÂÍÅÍÈÉ............................................................................................................................................ 3.1. Îáùèå ñâåäåíèÿ.......................................................................................................................................................................... 3.2. Ìåòîä áèñåêöèè........................................................................................................................................................................... (Ëàáîðàòîðíàÿ ðàáîòà ¹3).............................................................................................................................................................. 3.3. Ìåòîä õîðä....................................................................................................................................................................................... (Ëàáîðàòîðíàÿ ðàáîòà ¹4).............................................................................................................................................................. 3.4. Ìåòîä Íüþòîíà.................................................................................................................................................................................
(Ëàáîðàòîðíàÿ ðàáîòà ¹ 5)............................................................................................................................................................. 3.5. Ìåòîä ïðîñòûõ èòåðàöèé....................................................................................................................................................... (Ëàáîðàòîðíàÿ ðàáîòà ¹6).............................................................................................................................................................. 3.6. Êóðñîâàÿ ðàáîòà ïî äèñöèïëèíå è âàðèàíòû çàäàíèé......................................................................................... 3.7. Ïðîãðàììû äëÿ ðåøåíèÿ íåëèíåéíûõ óðàâíåíèé......................................................................................................... 4. ×ÈÑËÅÍÍÎÅ ÈÍÒÅÃÐÈÐÎÂÀÍÈÅ....................................................................................................................................................... 4.1. Ñîñòàâíûå ôîðìóëû ïðÿìîóãîëüíèêîâ, òðàïåöèé, Ñèìïñîíà.................................................................................. (Ëàáîðàòîðíàÿ ðàáîòà ¹6).............................................................................................................................................................. 4.2. Ôîðìóëà Ãàóññà. (Ëàáîðàòîðíàÿ ðàáîòà ¹7)............................................................................................................... Áèáëèîãðàôè÷åñêèé ñïèñîê........................................................................................................................................................
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.235.8 (0.01 с.) |

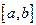 разбивают на четное
разбивают на четное 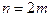 число отрезков длины
число отрезков длины  и на каждом из отрезков длины
и на каждом из отрезков длины  применяют соответствующую формулу. Таким образом получают составные формулы прямоугольников, трапеций и Симпсона.
применяют соответствующую формулу. Таким образом получают составные формулы прямоугольников, трапеций и Симпсона. ,
,  ,
,  , составные формулы имеют следующий вид:
, составные формулы имеют следующий вид: ;
; ;
;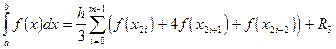 ,
, - îñòàòî÷íûå ÷ëåíû. При
- îñòàòî÷íûå ÷ëåíû. При 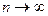 приближенные значения интегралов для всех трех формул (в предположении отсутствия погрешностей округления) стремятся к точному значению интеграла [1,7,8].
приближенные значения интегралов для всех трех формул (в предположении отсутствия погрешностей округления) стремятся к точному значению интеграла [1,7,8]. и
и  , получают приближенные значения интеграла
, получают приближенные значения интеграла  и
и  и за окончательные значения интеграла принимают величины:
и за окончательные значения интеграла принимают величины: - для формулы прямоугольников;
- для формулы прямоугольников;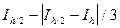 - для формулы трапеций;
- для формулы трапеций; - для формулы Симпсона.
- для формулы Симпсона.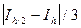 , а для формулы Симпсона
, а для формулы Симпсона  .
. (наибольшее значение шага
(наибольшее значение шага  , не превышающей заданную.
, не превышающей заданную.
 и коэффициенты
и коэффициенты  подобраны так, чтобы формула была точна для всех многочленов степени
подобраны так, чтобы формула была точна для всех многочленов степени  . Для приближенного вычисления интеграла по конечному отрезку
. Для приближенного вычисления интеграла по конечному отрезку  ; тогда квадратурная формула Гаусса принимает вид [2,8,12]
; тогда квадратурная формула Гаусса принимает вид [2,8,12]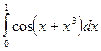









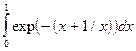














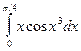


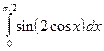
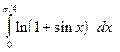


 ,
, ;
;  - узлы квадратурной формулы Гаусса;
- узлы квадратурной формулы Гаусса;  - гауссовы коэффициенты
- гауссовы коэффициенты 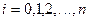 .
.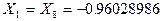 ,
,  ;
; ,
,  ;
; ,
,  ;
; ,
,  .
.