Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Истинностное значение формулыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пример Имеем формулы 1) 2) Невозможно определить истинностное значение формулы только по её виду. Для этого необходимо задать интерпретацию. Интерпретация = модель + значение свободной переменной, а модель = объектное множество + значение предикатного символа. Для формулы 1)зададим следующую интерпретацию: (I): А: 5>3 B: 3>0 C: 4<3 По соглашению о скобках имеем Следовательно ( Чтобы задать интерпретацию (I) Для формулы 2) необходимо: а) Задать значение предикатного символа
б) Задать объектное множество x,y в) Задать свободную переменную y=2 Ф(2)(I)=И Ф(10)(I)=Л
Таблица истинности Для формулы алгебры высказываний можно сказать какие значения она может принимать при конкретных значениях входящих в нее атомов, таким образом, можем построить таблицу истинности
Для формулы алгебры высказываний всегда можем построить такую таблицу. Для формулы алгебры предикатов этого сделать нельзя, т.к.: 1) Не все множества конечны 2) Нас интересуют все возможные множества Однако мы можем построить ограниченную таблицу истинности для частного случая, когда носителем алгебры предикатов является конечное множество: Пример Имеем одноместный предикат Ф(у) и объектное множество A={0,1}
В этом случае имеем 4 варианта формул определения одноместного предиката. Множество упорядоченных пар отображается на булево множество И, Л
{<00>, <01>, <10>, <11>} В случае объектного множества A={0,1, 2} имеем 8 вариантов определения одноместного предиката.
Выполнимость формул В алгебре высказываний формула называется выполнимой, если имеется набор истинности значений атомов, при которых значение формулы истинно. В алгебре предикатов формула выполнима, если существует интерпретация формулы, при которой она истинна.
Множество формул алгебры предикатов называется выполнимым, если существует интерпретация, в которой значения этих формул одновременно истинны. F = (A,B,C) Чтобы доказать, что формула выполнима, необходимо предъявить интерпретацию, в которой она истинна. В алгебре высказываний нужно предъявить строку таблицы истинности, в которой значение формулы истинно. Если ни в одной из интерпретаций формула не принимает истинного значения, то она является невыполнимой. Такая формула называется противоречие. Пример
Ни при каком значении атома А формула не принимает истинного значения Формулы, истинные в любой интерпретации называются общезначимыми или тавтологиями.
В случаем алгебры высказываний общезначимой будет формула, значение которой истинно во всех строках своей таблицы истинности. Примеры Логические законы 1) 2) 3)
В случае алгебры предикатов доказать общезначимость с помощью таблицы истинности нельзя, однако имеются примеры, для доказательства которых необходимо воспользоваться общими рассуждениями 1) Доказательство:
а)
Если предикат является истинным для всех значений индивидной переменной, то формула истинна. Б) Существуют значения индивидных переменных, при которых P(x) будет ложным
2) Доказательство а) Существуют значения индивидных переменных, для которых предикат P(y) истинен, тогда
б) Тогда
Для опровержения общезначимости необходимо привести хотя бы 1 интерпретацию или 1 строку из таблицы истинности, в которой формула ложна. Нахождение всех общезначимых формул – основная задача алгебры логики.
Отношение следования Следование формулы В из формулы А будем обозначать: 1) Формула В следует из формулы А если в любой интерпретации, в которой формула А истинна, формула В также истинна. Пример
Чтобы в этом убедиться, необходимо построить таблицу истинности. 2) Формула А следует из множества формул Г=
(Здесь и далее символ Пример
Убедиться можно аналогично, построив таблицу истинности.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 934; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.007 с.) |


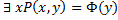

 , R
, R 

 – модель, на которую интерпретируются формулы
– модель, на которую интерпретируются формулы  , т.е. в нашем случае
, т.е. в нашем случае 
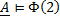 – истинное значение
– истинное значение – ложное значение
– ложное значение

 {И, Л}
{И, Л}



 – закон отрицания отрицания
– закон отрицания отрицания – закон отрицания противоречия
– закон отрицания противоречия – закон исключенного третьего
– закон исключенного третьего
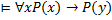


 для
для  , т.е.
, т.е. 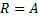

 также истинно, т.к.
также истинно, т.к.  истинно при любых значениях объектных переменных
истинно при любых значениях объектных переменных имеем импликацию вида И
имеем импликацию вида И  И=И
И=И

 т.к. ложная посылка импликацию дает истину.
т.к. ложная посылка импликацию дает истину.


 , т.к. заключение истинно
, т.к. заключение истинно , для
, для 



 если во всех интерпретациях, в которых формулы
если во всех интерпретациях, в которых формулы  истинны, формула А также истинна.
истинны, формула А также истинна. 
 , …
, …  И
И будет соответствовать словесной формулировке «если…, то…»)
будет соответствовать словесной формулировке «если…, то…»)