
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полнота исчисления предикатовСодержание книги
Поиск на нашем сайте
Рассмотрим полноту исчисления предикатов. Определение: Множество Т называется полным если для любой формулы исчисления предикатов существует вывод этой формулы из Т, либо существует вывод отрицания этой формулы Т.е. для "Е ∈ ИП существует вывод Т ⊢ Е или Т ⊢ Е Теорема о выполнимости: Всякое непротиворечивое множество выполнимо Г – непротиворечиво => Г – выполнимо Рассмотри вспомогательную Лемму для доказательства теоремы.
Пусть существует множество S и множество φ Рассмотрим иерархию множеств S c Процесс включения будет продолжаться пока не получится некоторое максимальное непротиворечивое множество включающее S. Его получим т.к. множество всех формул больше чем любое множество непротиворечивых формул.
Т.е. существует формула, Ψ для которой существует По правилу введения отрицания можем записать что Полное т.е.
Теорема Всякое непротиворечивое множество выполнимо, следовательно, существует такая интерпретация, при которой все формулы множества истинны.
I: <M, М = {x1,…,xn,y1,…,yn}
Pn(x1,…,xn)(I)=
Р
Доказать, что на модели <M,
Доказательство: (По индукции) 1) База индукции А = Pn(x1,…,xn) – по определению 2) Шаг индукции 1. А = А1 2. А = А1 3. А = А1 & А2 4. А = А1 5. А = А1 6. A = 7. A =
Докажем, что если для формул A1, А2 выполняется: А1(I)= И, А2(I)= И То для формулы А выполняется: А(I)= И
1. А = А1 Необходимость Докажем, что для А = А1 теорема выполняется. А(I)= И
Достаточность T ⊢ А т.к. Т – полное, непротиворечивое множество, то: Т ⊢ А1
3. А = А1 & А2 Необходимость А(I)= И
Достаточность (от противного) Т ⊢ А1 & А2. Пусть А1 & А2 = А = Л Т.к. Т ⊢ А1 & А2 А1 = Л или А2 = Л Противоречие!
В рассматриваемой интерпретации для любого значения предиката значение формулы истинно, если А(I)=И Поскольку S Теорема (о полноте) Любая общезначимая формула доказуема. |= E
Доказательство: ЕI=И
Другие теоремы
Теорема (о непротиворечивости) Любое выполнимое множество формул является непротиворечивым. Ф – выполнимо
Доказательство: (от противного) Пусть Ф – выполнимо, но противоречиво Ф ⊢ (ψ & ψ)
Но т.к. любая доказуемая формула является общезначимой
(связаны отношением следования) Т.к. (ψ & ψ)I=Л => (Ф1) =Л – невыполнимо
Теорема Мальцева (теорема компактности) Если множество выполнимо, то выполнимо любое его конечное подмножество. Ф – выполнимо
Необходимость: Доказательство опустим.
Достаточность: Предположим, что все S- выполнимы, а Ф – невыполнимы
Теорема (об адекватности) Если формула ϕ следует из множества формул Ф, то формула ϕ выводится из Ф. Ф
Необходимость: Ф
Достаточность: Уже доказывали (теорема 1) Ф ⊢ Семантический и синтаксический подходы эквивалентны как в исчислении предикатов, так и в исчислении высказываний.
Алгоритмические модели Понятие алгоритма Алгоритм – последовательность действий приводящая к получению определенного результата из исходных данных за конечное число действий. Такое определение алгоритма является интуитивным понятием. Алгоритмические проблемы: 1. Алгоритмическая разрешимость. Имеет ли данная задача алгоритм решения? 2. Наибыстрейший алгоритм решения. Определение нижней границы сложности решения. В рамках интуитивного определения алгоритма нельзя разрешить данные алгоритмические проблемы, поэтому рассмотрим, что именно в интуитивном понятии алгоритма нуждается в уточнении. 1. Что такое данные (алгоритмический объект) 2. Память. Способ хранения и представления данных 3. Элементарное действие, команда 4. Последовательность порождения операций, шагов 5. Что есть результат 6. Способ реализации Однозначного определения данных понятий для алгоритма не было найдено. Таким образом алгоритм есть фундаментальное интуитивно ясное, но неопределяемое понятие. Поэтому в теории алгоритмов принят подход, основанный на конкретной алгоритмической модели. Алгоритмическая модель – подкласс алгоритмов, в которых строго определены понятия алгоритма. При этом используемые алгоритмические модели универсальны(это недоказуемое утверждение) т.е. алгоритм в любой разумной алгоритмической модели имеет аналог в рамках данной. Классы моделей: 1. Класс как описание некоторого технического устройства: машина Тьюринга, машина прямого доступа, машина Поста. 2. Описание алгоритма как некоторого класса функций с определенными способами их образования: частично рекурсивные функции(исторически первая формализация понятия алгоритма). 3. Набор правил по преобразованию слов: алгорифм Маркова.
Машины Тьюринга
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 666; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.01 с.) |

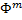 Для любого непротиворечивого множества S существует более полное непротиворечивое множество включающее в себя множество S т.е. S c T где Т – полное множество
Для любого непротиворечивого множества S существует более полное непротиворечивое множество включающее в себя множество S т.е. S c T где Т – полное множество S при этом S
S при этом S  φ причем если φ добавить в S, то
φ причем если φ добавить в S, то  – непротиворечиво
– непротиворечиво c
c  …
…  - даст уже противоречивое множество, где "f
- даст уже противоречивое множество, где "f 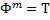
 >, где М – объектное множество, δ – множество отношений, <M,
>, где М – объектное множество, δ – множество отношений, <M, 
 Т – полное, непротиворечивое множество
Т – полное, непротиворечивое множество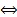 T
T  A
A А2
А2 А2
А2 А2
А2 x A1
x A1 x A1
x A1 А1(I)= Л
А1(I)= Л  найдется формула ψ, для которой можно вывести противоречие.
найдется формула ψ, для которой можно вывести противоречие. существует некая конечная последовательность формул
существует некая конечная последовательность формул  ,
, 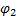 , …, ψ & ψ
, …, ψ & ψ 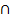 {
{  } ⊢ ψ & ψ //по теореме о дедукции//
} ⊢ ψ & ψ //по теореме о дедукции//  …(
…(
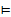 (
( …
…  ψ & ψ
ψ & ψ

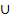 {
{ 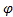 } – невыполнимо
} – невыполнимо 


