
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
СДНФ. Совершенно дизъюктивная нормальная форма.Содержание книги
Поиск на нашем сайте СДНФ – называется представление логической функции в виде дизъюнкций элементарных конъюнкций F= C1 V C2 V…V Cs, где Ci –элементарная конъюнкция Элементарная конъюнкция имеет следующий вид: C= L1 & L2 & … & Ln , где L1=x или L1= x.
СКНФ. Совершенно конъюктивная нормальная форма. СКНФ – называется представление логической функции в виде конъюнкций элементарных дизъюнкций. F= D1 & D2 & … & Dn, где D1 - элементарная дизъюнкция, Элементарная дизъюнкция имеет следующий вид: D= L1 V L2 V … V Ln, где L1=x или L1= x. Теорема 1. Любая логическая функция может быть представлена в виде СДНФ. Доказательством теоремы является алгоритм, который позволяет из любой логической функции получить СДНФ. Пусть логическая функция задана таблицей истинности.
Берем строчки, где значение функции =1 и составляем из них элементарные конъюнкции, причем если значение переменной в таблице 1, то она входит в элементарную конъюнкцию в прямой форме, иначе входит отрицание этой переменной. СДНФ: (x & y & z) V (x & y & z) V (x & y & z) Полученная формула является ДНФ, кроме того она имеет значение совпадающее со значением функции f. Поскольку если мы берем набор, который соответствует значению 1, то какая-то элементарная конъюнкция имеет значение 1. Противоречивая формула может быть также представлена в ДНФ. Пример противоречивой формулы в ДНФ: (x & x) V (y & y) V (z & z) Таким образом мы доказали теорему о том, что любая логическая функция может быть представлена в виде ДНФ. А также теорема доказывает, что логическая функция может быть представлена выражением элементарных унарных и бинарных логических значений.
Теорема 2. Любая логическая функция может быть представлена в виде СКНФ. Доказательством теоремы является алгоритм, который позволяет из любой логической функции получить СКНФ. Пусть логическая функция задана таблицей истинности.
Берем строчки, где значение функции =0 и составляем из них элементарные дизъюнкции, причем если значение переменной в таблице 0, то она входит в элементарную дизъюнкцию в прямой форме, иначе входит отрицание этой переменной. СКНФ: (x V y V z) & (x V y V) & (x V y V z) & (x V y V z) & (x V y V z) Полученная формула является КНФ, кроме того она имеет значение совпадающее со значением функции f. Поскольку если мы берем набор, который соответствует значению 0, то какая-то элементарная конъюнкция имеет значение 0. Противоречивая формула может быть также представлена в КНФ. Пример противоречивой формулы в КНФ: (x V x) & (y V y) & (z V z) Полиномы Жегалкина F= C 1 Для того, чтобы получить полином, нужно в СДНФ-е выразить «ИЛИ» через «И» / «НЕ» в соответсвии с формулами и затем, с помощью преобразований, привести к соответсвующему виду. Исчисление высказываний Общее понятие о логическом исчислении Для определения логического исчисления необходимо задать: 1. Язык 2. Правила вывода 3. Аксиомы Рассмотрим пример определения логического исчисления: 1. Язык a. Алфавит А b. Формула (будем считать, что в нашем исчислении формулой является произвольная последовательность букв А) 2. Правила вывода 3. Аксиомы:
Таким образом, мы получили исчисление, в котором может появиться произвольная последовательность букв Чтобы исчисление было содержательным оно должно удовлетворять двум требованиям: 1. Правила вывода должны быть корректными (при истинных посылках, истинные следствия) 2. Аксиомы должны быть общезначимы. Исторически сложившиеся содержательное исчисление высказываний: Язык совпадает с языком алгебры высказываний, содержит пропозициональные буквы, пропозициональные связки. Формулы совпадают с формулами алгебры высказываний.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 517; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |

 C2
C2 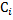 - элементарная конъюнкция
- элементарная конъюнкция
 (ноль посылочные правила)
(ноль посылочные правила)


