
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частично-рекурсивные функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение частично-рекурсивных функций Будем рассматривать функции натурального аргумента: f(x), где x
всюду определенная функция частично определенная функция
Определим три базовые функции: 1. Ноль-функция 0(х)=0 Всюду определенная функция, значение которой всегда равна нулю. 2. Функция следования s(x)=x+1 3. Функция взятия аргумента
m –m-местная функция, n – порядковый номер аргумента, значению которого равно значение функции. Определим три типа операций: 1. S – суперпозиция: Пусть нам даны функции: g( Тогда можно определить новую функцию: f( 2. R - примитивная рекурсия: Пусть нам даны функции: g( Тогда может быть определена новая (n+1)-местная функция: f( т.е. функция определяется через себя же. Предположим, что некоторое значение Как S, так и R, будучи применимыми ко всюду определенным функциям, дают всюду определенную функцию. 3. M – операция минимизации: Пусть дана n-местная функция g( g( Решать будем следующим образом: будем перебирать значения y, начиная с 0. Как только получим первое значение, которое удовлетворяет уравнению, мы получим минимальное решение данного уравнения.
Частично рекурсивные функции (ЧРФ) – это функции полученные с помощью конечного числа использований операций R, M, S к функциям O(x), S(x), Данное определение можно представить в следующем виде: 1) 2) 3) 4) 5) Других ЧРФ нет Примеры ЧРФ 1.
2. Функция
3. 4.
5. Sg(x) =
6.
7.
8.
9.
Фактически любая функция, которую можно вычислить может быть получена путем использования операций S,M,R к функциям O(x), S(x), Тезис Чёрча В классе ЧРФ можно выделить 2 подкласса:
Существует ли функция принадлежащая классу Функция Аккермана
Эта функция возрастает быстрее чем любая функция принадлежащая к классу Тезис Черча: Всякая вычисляемая(рекурсивная) функция является ЧРФ. Это утверждение принципиально недоказуемо т.к. есть принцип неопределяемый класс вычислимых функций.
Соотношение между классами «Т» и «Ч» Из тезисов Тьюринга и Черча следует что класс функций вычислимых по Тьюрингу совпадает с классом ЧРФ (в том случае если эти тезисы верны) Т.е. если Это можно проверить, т.к. оба этих класса являются строго определенными. Вычислимость по Тьюрингу ЧРФ Для того чтобы доказать что Для того чтобы доказать первое утверждение необходимо доказать что: 1) 2) Операций S, M, R являются вычислимыми по Тьюрингу. Докажем второй пункт, а первый это практика? Построим машину вычисляющую суперпозицию
Вычислимость рекурсии Существуют
Вычислимость минимизации
Существует доказательство что T с Ч Совпадение классов ЧРФ и функций вычисляемых по Тьюрингу показывает важное косвенное свидетельство истинности тезисов Тьюринга и Черча. Нумерации наборов чисел и слов Нумерация пар чисел
Где Упорядочиваем пары x+y=n по n, а внутри скобок < > упорядочивание происходит следующим образом: Например для x+y=n: Т.е. начало будет выглядеть так: При таком способе упорядочивания можем ввести функцию
Такая нумерация называется Канторовской. Также возможно по известному номеру определить x и y
Для
9.2 Наборов из n чисел Тогда в общем случае
9.3 Нумерация множества M=N&N2&… Упорядочим элементы множества M которое имеет вид
Нумерация слов Нумеровать можно не только наборы чисел, но и наборы слов. 1. Пусть есть алфавит Можно интерпретировать каждый символ r-ичным числом, тогда слово будет представлено s-значным числом вида 2. Пусть количество символов в алфавите бесконечно и пусть такое бесконечное множество является счётным. Тогда алфавит А как пронумеровать набор чисел было показано выше. Обозначим канторовский номер слова в счетном алфавите следующим образом Для пустого символа канторовский номер будет равен нулю
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.80.121 (0.009 с.) |

 N
N
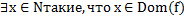
 , где
, где и
и  (
( …
…  (
( ))
))  S(g,
S(g,  )
) =g(
=g( ) – n-местная функция и h(
) – n-местная функция и h( – (n+2)-местная функция.
– (n+2)-местная функция. =R(g,h)=
=R(g,h)=  =
=  ,
, при
при  значение функции
значение функции  будет не определено (f(
будет не определено (f( f(y) при y>
f(y) при y>  ):
): =
= 
 =M(g(
=M(g( (Под x везде понимаем множество
(Под x везде понимаем множество 
 , где
, где  - класс ЧРФ
- класс ЧРФ




 является рекурсией от функций
является рекурсией от функций



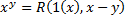











 – целая часть от деления
– целая часть от деления - остаток от деления
- остаток от деления - отлична от нуля в конечном количестве точек
- отлична от нуля в конечном количестве точек - количество простых чисел < x
- количество простых чисел < x – простое число
– простое число - общерекурсивные функции
- общерекурсивные функции - примитивно рекурсивные функции - функции, полученные без операции минимизации
- примитивно рекурсивные функции - функции, полученные без операции минимизации
 которую нельзя было бы получить с помощью операций R и S?
которую нельзя было бы получить с помощью операций R и S?


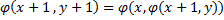

 т.к. нашлась функция которая является
т.к. нашлась функция которая является  то тезис Тьюринга или Черча не верен, либо они оба не верны.
то тезис Тьюринга или Черча не верен, либо они оба не верны. необходимо доказать что 1) Ч с Т и 2) Т с Ч
необходимо доказать что 1) Ч с Т и 2) Т с Ч являются функциями вычислимыми по Тьюрингу.
являются функциями вычислимыми по Тьюрингу. т.е. существуют
т.е. существуют 

















 0
0


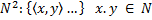
 - упорядоченная пара
- упорядоченная пара

 - характеризующая номер упорядоченной пары
- характеризующая номер упорядоченной пары – канторовский номер
– канторовский номер







 - все возможные наборы натуральных чисел т.е. произвольный упорядоченный набор чисел
- все возможные наборы натуральных чисел т.е. произвольный упорядоченный набор чисел где n – количество чисел в наборе
где n – количество чисел в наборе
 …
… множество всевозможных слов и символов этого алфавита
множество всевозможных слов и символов этого алфавита 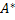 и хотим упорядочить слова т.е. однозначно поставить каждому слову в соответствие номер.
и хотим упорядочить слова т.е. однозначно поставить каждому слову в соответствие номер.  - слово из
- слово из 

 называется счётным алфавитом. Можно поставить каждому символу в соответствие номер. Тогда слово может быть интерпретировано как набор чисел
называется счётным алфавитом. Можно поставить каждому символу в соответствие номер. Тогда слово может быть интерпретировано как набор чисел  .
. где
где  - канторовский номер набора чисел.
- канторовский номер набора чисел.



