
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмически неразрешимые проблемыСодержание книги
Поиск на нашем сайте Понятие массовой и индивидуальной алгоритмической проблемы. Определение алгоритмически неразрешимой проблемы Под массовой алгоритмической проблемой будем понимать бесконечные серии подобных задач, которые отличаются друг от друга только набором значений параметров. 1)
2) Для функции
Будем рассматривать алгоритмические проблемы, которые дают ответ «Да» или «Нет». Такие задачи называют задачами распознавания. С каждой задачей распознавания может быть связана характеристическая функция.
Если характеристическая функция является вычислимой, то соответствующая массовая проблема является алгоритмически разрешимой, в противном случае является не разрешимой.
Способы доказательства алгоритмической неразрешимости Проблема самоприменимости МТ Пусть есть некоторая машина Тьюринга: Т Применима ли машина к конфигурации Код(Т)
Пример самоприменимой МТ:
Пример не самоприменимой МТ:
Проблема заключается в определении для любой машины по её коду является ли она самоприменимой или нет. Докажем что не существует МТ способной это определить. Доказательство: будем доказывать от противного. Пусть существует машина Тьюринга М которая решает проблему самоприменимости.
Сконструируем машины
Т.е. машина Является ли машина Пусть
Тогда предполагая, что машина
Из этого следует что машины
2.Сводимость проблем Пусть существуют две алгоритмические проблемы
Тогда говорят, что задача(проблема) Тогда справедлива следующая теорема: Если задача Доказательство: Пусть задача
И по определению сводимости имеем для задачи
Таким образом получили противоречие. Следовательно,
3. Проблема останова Есть произвольная машина Т и произвольное слово Р
Остановится ли машина с начальной конфигурацией Проблема самоприменимости сводится к проблеме останова т.к. выбрав в качестве слова Р=Код(Т) получим проблему самоприменимости. Т.к. проблема самоприменимости является не разрешимой, то и проблема оснатова также является алгоритмичести не разрешимой. 11.3 Проблема «x Î Wx»
· Определить для произвольного числа X принадлежит ли оно области определения ЧРФ стоящей под номером X.
Доказательство: Рассмотрим характеристическую функцию
И функцию следующего вида:
Пусть g(x) вычислима, тогда она стоит в ряде ЧРФ под некоторым номером n т.е. Определена ли функция g(x) в точке n? Пусть g(n) определена, это значит что:
Т.е. Если предположить, что g(n) не определена тогда:
Следовательно исходная посылка, что g(n) вычислима не верна и функция g(n) не вычислима, а это значит, что функция f(x) также не вычислима.
· Рассмотрим две функции отвечающие двум проблемам:
Обе эти функции не вычислимы. Рассмотрим функции
В этом случае считается, что функция g(x) является более невычислимой, чем f(x), а проблема
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 697; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.008 с.) |

 - индивидуальная проблема
- индивидуальная проблема для
для 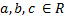 – это массовая проблема
– это массовая проблема :
: индивидуальная проблема
индивидуальная проблема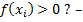 массовая проблема
массовая проблема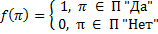 , где
, где  - набор параметров из П – массовая проблема
- набор параметров из П – массовая проблема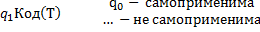



 которая будет включать в себя все команды машины М + ещё две новых команды:
которая будет включать в себя все команды машины М + ещё две новых команды:
 , где
, где  - новое заключительное состояние
- новое заключительное состояние получили противоречие
получили противоречие
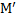 существовать не может
существовать не может  начальное предположение о существовании машины М решаемой проблему самоприменимости ложно
начальное предположение о существовании машины М решаемой проблему самоприменимости ложно  . И существует некоторая функция которая преобразует набор
. И существует некоторая функция которая преобразует набор  , причём так, что:
, причём так, что: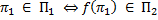

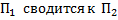
 сводится к задаче
сводится к задаче  и задача
и задача  – вычислима
– вычислима - снова вычислима
- снова вычислима


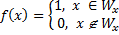
 - вычислима если
- вычислима если  – не вычислима
– не вычислима


 т.е. g(n) определена
т.е. g(n) определена 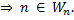 Снова получили противоречие.
Снова получили противоречие.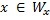
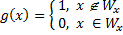 - отвечает проблеме
- отвечает проблеме 
 вида:
вида: - также является не вычислимой
- также является не вычислимой - данная функция уже является вычислимой
- данная функция уже является вычислимой


