
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нумерация алгоритмов. Невычислимые функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Нумерация машин Тьюринга В качестве внешнего алфавита возьмём объединение алфавитов всех возможных машин Тьюринга.
Внутренний и внешний алфавит являются бесконечными и счётными.
Упорядочим символы в этом алфавите
Каждому символу можно сопоставить номер При таком общем алфавите каждая машина Тьюринга будет отличаться только набором команд
Упорядочим команды по левой части в лексикографическом порядке в соответствии с их следованием в перечислении и запишем в одно слово
Слово состоит из пятёрок символов, которые имеют свою структуру Существует достаточный набор признаков по которым можно отличить слово, которое является программой МТ от слова которое программой не является (достаточно признаков для того чтобы однозначно это определить) Заменим каждый символ соответствующим номером
Можно упорядочить все наборы машин Тьюринга в порядке возрастания их канторовских номеров.
Расположены по мере возрастания, но не подряд, т.е. к примеру, такого вида:
Канторовский номер не соответствует номеру машины Тьюринга. Упорядочивание является эффективным, т.е. можно по коду МТ определить её номер и по номеру восстановить код и программу МТ Определение номера по коду можно представить в виде следующего алгоритма
А восстановление кода МТ по номеру можно с помощью следующего алгоритма.
Перечисление МТ позволяет построить эффективное перечисление ЧРФ т.к. все ЧРФ могут быть … с помощью МТ Также по коду МТ можно восстановить ЧРФ т.е. перечисление МТ является также перечислением ЧРФ. ЧРФ может быть вычислена бесконечным количеством машин Тьюринга. Существование эффективного перечисления дает два следствия: 1. Рассмотрим функцию
Функция Вывод: Существует бесконечное множество невычислимых функций. 2. Существование универсальной функции. Пусть существует класс
1) 2) Т.е. функция, содержащая в себе все функции одного класса.
Теорема 1: О существовании универсальной функции класса одноместный ЧРФ Рассмотрим класс одноместных ЧРФ И рассмотрим функцию Докажем, что функция 1)
Функция является вычислимой т.к. существует алгоритм её вычисления 2) Выберем некоторую функцию
Следствие Для класса n-местных ЧРФ Доказательство: 1. 2. Берем произвольную n-местную ЧРФ
И определим новую функцию от канторовского номера
Для классов
Теорема 2: Не существует универсальной функции для класса общерекурсивных функций
Теорема 3: Для класса n-местных примитивно рекурсивных функций существует универсальная
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 795; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |


 - множество всех возможных внутренних состояний МТ
- множество всех возможных внутренних состояний МТ

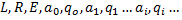 - перечисление символов объединенного алфавита
- перечисление символов объединенного алфавита

 - код машины Тьюринга
- код машины Тьюринга


 Р
Р

 Ф(р)=1
Ф(р)=1


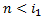







 всюду определена и не является ни одной из функций в перечислении ЧРФ. Т.к в перечисление ЧРФ попадают все возможные ЧРФ, которые в свою очередь по тезису Черча являются вычислимыми следует, что данная функция является невычислимой. Таким образом, функция
всюду определена и не является ни одной из функций в перечислении ЧРФ. Т.к в перечисление ЧРФ попадают все возможные ЧРФ, которые в свою очередь по тезису Черча являются вычислимыми следует, что данная функция является невычислимой. Таким образом, функция 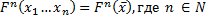
 - называется универсальной функцией класса F если:
- называется универсальной функцией класса F если:
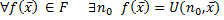


 является универсальной функцией для класса одноместных ЧРФ.
является универсальной функцией для класса одноместных ЧРФ.


 ЧРФ
ЧРФ из класса ЧРФ
из класса ЧРФ - по определению функции U
- по определению функции U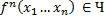 существует
существует  - местная универсальная функция
- местная универсальная функция 
 т.к. является суперпозицией ЧРФ
т.к. является суперпозицией ЧРФ 

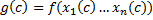 – все переменные выражены только через канторовский номер
– все переменные выражены только через канторовский номер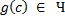 т.к. является суперпозицией
т.к. является суперпозицией 

 – универсальная одноместная функция, тогда
– универсальная одноместная функция, тогда - универсальная ЧРФ
- универсальная ЧРФ справедливы следующие теоремы:
справедливы следующие теоремы:
 -местная общерекурсивная функция т.е. для
-местная общерекурсивная функция т.е. для 



