Применение производной в исследовании функций

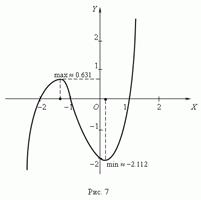
Связь между непрерывностью и дифференцируемостью функции. Если функция f (x) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной.

С л е д с т в и е. Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.

Достаточные признаки монотонности функции.

Если f ’(x) > 0 в каждой точке интервала (a, b), то функция f (x) возрастает на этом интервале.

Если f ’(x) < 0 в каждой точке интервала (a, b), то функция f (x) убывает на этом интервале.

Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.

Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.

Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум (минимум или максимум, рис.5 а, б).

Необходимое условие экстремума. Если x 0 - точка экстремума функции f (x) и производная f’ существует в этой точке, то f’ (x 0) = 0.

Эта теорема - необходимое условие экстремума. Если производная функции в некоторой точке равна 0, то это не значит, что функция имеет экстремум в этой точке.

Достаточные условия экстремума.

Если производная при переходе через точку x 0 меняет свой знак с плюса на минус, то x 0 - точка максимума.

Если производная при переходе через точку x 0 меняет свой знак с минуса на плюс, то x 0 - точка минимума.

План исследования функции. Для построения графика функции нужно:

1) найти область определения и область значений функции,

2) установить, является ли функция чётной или нечётной,

3) определить, является ли функция периодической или нет,

4) найти нули функции и её значения при x = 0,

5) найти интервалы знакопостоянства,

6) найти интервалы монотонности,

7) найти точки экстремума и значения функции в этих точках,

8) проанализировать поведение функции вблизи “особых” точек

и при больших значениях модуля x.

Пример на случай, если заставит решить при нем какое-нибудь задание, но если не хотите - удалите

П р и м е р. Исследуйте функцию f (x) = x 3 + 2 x 2  x  2 и постройте график.

 

Р е ш е н и е. Исследуем функцию по вышеприведенной схеме.

 

1) область определения x  R (x – любое действительное число);

область значений y  R, так как f (x) – многочлен нечётной

степени;

 

2) функция f (x) не является ни чётной, ни нечётной

(поясните, пожалуйста);

 

3) f (x) – непериодическая функция (докажите это сами);

 

4) график функции пересекается с осью Y в точке (0, – 2),

так как f (0) =  2; чтобы найти нули функции нужно

решить уравнение: x 3 + 2 x 2  x  2 = 0, один из корней

которого (x = 1) очевиден. Другие корни находятся

(если они есть!) из решения квадратного уравнения:

x 2 + 3 x + 2 = 0, которое получено делением многочлена

x 3 + 2 x 2  x  2 на двучлен (x – 1). Легко проверить,

что два других корня: x 2 = 2 и x 3 = 1. Таким образом,

нулями функции являются: 2, 1 и 1.

 

5) Это значит, что числовая ось делится этими корнями на

четыре интервала знакопостоянства, внутри которых

функция сохраняет свой знак:

Этот результат может быть получен разложением

многочлена на множители:

 

x 3 + 2 x 2  x  2 = (x + 2) (x + 1 (x – 1)

 

и оценкой знака произведения методом интервалов.

 

6) Производная f’ (x) = 3 x 2 + 4 x 1 не имеет точек, в которых

она не существует, поэтому её область определения R (все

действительные числа); нули f’ (x) – это корни уравнения:

3 x 2 + 4 x  1 = 0.

Полученные результаты сведены в таблицу:

Экстремум функции

Необходимое условие экстремума

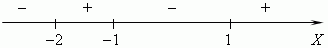
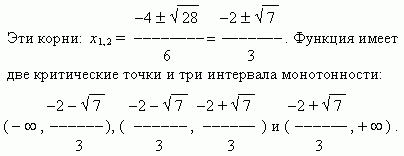
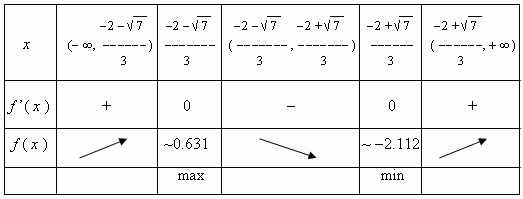
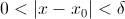Функция g(x) в точке имеет экстремум(максимум или минимум), если функция определена в двухсторонней окрестности точки и для всех точек x некоторой области: , выполнено соответственно неравенство

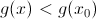(в случае максимума) или (в случае минимума).

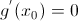Экстремум функции находиться из условия: , если производная существует, т.е. приравниваем первую производную функции к нулю.