Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайной называют такую величину,которая принимает значения в зависимости от степени случайных обстоятельств.Случайные величины классифицируют на дискретные и непрерывные.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дискретной(прерывной)называют случайную величину,которая принимает отдельные,изолированные возможные значения с определенными вероятностями.Число возможных значений дискретной случайной величины может быть конечной и бесконечной. Непрерывной случайной величиной называют случайную величину,которая может принимать все значения из некоторого конечного или бесконечного промежутка.Множество возможных значений непрерывной случайной величин бесконечно и несчетно. Закон распределения случайной величины называют всякое отношение,устанавливающее связь между возможными значениями случайной величины и соответсвующим им вероятностями.Закон распределения может имень разные формы. 17)Математическое ожидание,случайной величины-это сумма произведений всех случайных величин.Математическое ожидание X(ω) определяется как интеграл Лебега по отношению к вероятностной мере Р в исходном вероятностом пространстве.EX(ω)=∫X(ω) P(dω) Дисперсия-мера рассеивания(отклнения от среднего).Квадратный корень из диссперсии,равный ϭ,называется среднеквадратичным отклонением.Дисперсия =D(X)=M( 18)Непрерывная случайная величина принимает любое значение внутри некоторого интервала.Задается формулой dP=f(x)dx,где f(x)-плотность вероятности,или функция распределения вероятностей.Она показывает, как изменяется вероятность,отнесенная к интегралу dx случайной величины, в зависимости от значения спмой этой величины:f(x)=dP/dx 19)нормальное распределение,важнейшее распределение непрерывного типа,также называемое гаусовым распределением,которое задается формулой распределения:f(x)= Нормально распределение играет важную роль во многих областях знаний,особенно в статистичекой физике.Физическая величина,подверженная влиянию значительного числа,независимых факторов,способных вносить с равной погрешностью положительное и отрицательное отклонения,вне зависимости от природы этих случайных факторов,часто подчиняется нормальному распределению,поэтому из всех распределений в природе чаще всего встречается нормальное.Оно зависит от двух параметров, смещения и масштаба,т.е. является с материальной точки зрения не одним распределением,а целым их семейством.Значение параметров соответствуют значениям среднего(материального ожидания)и разброса(стандартного отклонения) 20)Математическая статистика-наука,разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.Во многих своих раздлах опирается на теорию вероятностей,позволяющую оценить надежность и точность выводов,делаемых на основании ограниченного статистического материала о ней имеет смысл вспомнить,если: -имеется случайный эксперимент,свойста которого частично или полностью неизвестно. -мы е\умеем воспроизводить этот эксперимент в одних и тех же условиях некоторое число раз. Генеральная совокупность,генеральная выборка-совокупность всех объектов,относительно которых ученый намерен делать выводы при изучении конкретной проблеиы.Генеральная совокупность состоит из всех объектов,которые подлежат изучению.Состав генеральной совакупности зависит от целей исследования. Выборка-множество случаев,с помощью определенной процедуры выбранных из генееральной совокупности для учений в иследовании. Основные понятия математической статистики. Генеральная совокупность и выборка. Математическая статистика занимается установлением закономерностей, которым подчинены массовые случайные явления, на основе обработки статистических данных, полученных в результате наблюдений. Двумя основными задачами математической статистики являются: - определение способов сбора и группировки этих статистических данных; - разработка методов анализа полученных данных в зависимости от целей исследования, к которым относятся: а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости от других случайных величин и т.д.; б) проверка статистических гипотез о виде неизвестного распределения или о значениях параметров известного распределения. Для решения этих задач необходимо выбрать из большой совокупности однородных объектов ограниченное количество объектов, по результатам изучения которых можно сделать прогноз относительно исследуемого признака этих объектов. Определим основные понятия математической статистики. Генеральная совокупность– все множество имеющихся объектов.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1885; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (5.615 с.) |

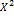 )-(M(X)). Среднее квадратическое отклонение ϭ(X)=√D(X) использованное чтобы оценивать рассеяние случайной величины в единизах той же размерности.
)-(M(X)). Среднее квадратическое отклонение ϭ(X)=√D(X) использованное чтобы оценивать рассеяние случайной величины в единизах той же размерности.