
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды погрешностей измерений и их оценка.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Определение погрешности В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы. · Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:
· Средняя квадратическая погрешность:
· Средняя квадратическая погрешность среднего арифметического:
Виды представления: По способу измерения · Погрешность прямых измерений - вычисляется по формуле
где: · Погрешность косвенных воспроизводимых измерений — погрешность вычисляемой (не измеряемой непосредственно) величины: Если
· Погрешность косвенных невоспроизводимых измерений - вычисляется по принципу прямой погрешности, но вместо Погрешность измерения и принцип неопределенности Гейзенберга Принцип неопределенности Гейзенберга устанавливает предел точности одновременного определения пары наблюдаемых физических величин, характеризующих квантовую систему, описываемых не коммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Таким образом, в квантовой механике постулируется принципиальная невозможность одновременного определения с абсолютной точностью некоторых физических величин. Этот факт накладывает серьёзные ограничения на применимость понятия «истинное значение физической величины. Корреляционный и регрессивный анализ. Функциональная и корреляционная зависимость. Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации). [1][2] Область применения Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи. Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных. Регрессио́нный (линейный) анализ — статистический метод исследования влияния одной или нескольких независимых переменных Цели регрессионного анализа 1. Определение степени детерминированностивариации критериальной (зависимой) переменной предикторами (независимыми переменными) 2. Предсказание значения зависимой переменной с помощью независимой(-ых) 3. Определение вклада отдельных независимых переменных в вариацию зависимой Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 755; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.146 (0.007 с.) |


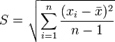


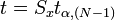 ;
;  — стандартная ошибка среднего (выборочное СКО, деленное на корень из количества измерений
— стандартная ошибка среднего (выборочное СКО, деленное на корень из количества измерений  ), а
), а  — квантиль распределения Стьюдента для числа степеней свободы
— квантиль распределения Стьюдента для числа степеней свободы  и уровня значимости
и уровня значимости  ;
;  — абсолютная погрешность средства измерения (обычно это число равное половине цены деления измерительного прибора).
— абсолютная погрешность средства измерения (обычно это число равное половине цены деления измерительного прибора). , где
, где  — непосредственно измеряемые независимые величины, имеющие погрешность
— непосредственно измеряемые независимые величины, имеющие погрешность  , тогда:
, тогда:
 на зависимую переменную
на зависимую переменную  . Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения.
. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения.


