
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок операций при обработке результатов серии измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При прямых измерениях: 1. Результаты каждого измерения записать в таблицу. 2. Вычислить среднее значение из n измерений
3. Найти погрешности отдельных измерений
4. Вычислить квадраты погрешностей отдельных измерений (D x 1)2, (D x 2)2,..., (D xn)2. 5. Оценить среднеквадратичную погрешность среднего значения
6. Определить коэффициент Стьюдента t na (по таблице) для доверительной вероятности Р = 0,95 и числа произведенных измерений n. 7. Найти случайную погрешность результата измерений:
8. Если случайная погрешность результата измерений D x окажется сравнимой[2] с систематической (погрешностью прибора D x пр), то в качестве погрешности результата измерений следует взять величину
9. Окончательный результат записать в виде:
10. Оценить относительную погрешность результата измерений
При косвенных измерениях: 1. Для каждой непосредственно измеренной величины (X 1, X 2,..., X m), входящей в расчетную формулу для определения X (X = f (X 1, X 2,..., X m)), провести обработку в описанной выше последовательности, т.е. вычислить средние арифметические значения 2. При необходимости учесть систематическую (приборную) погрешность каждой серии измерений
где индекс i относится к соответствующей измеренной величине, а D X пр i – систематическая погрешность прибора, используемого для измерения Хi. 3. Вычислить наиболее вероятное значение X:
4. Вычислить частные производные 5. Определить абсолютную погрешность косвенного измерения X по общей формуле:
Здесь и выше m – число независимых непосредственно измеренных величин. Округлить полученный результат до двух значащих разрядов. 6. Записать окончательный результат в виде
7. Определить относительную погрешность косвенного измерения X:
Правила представления результата измерения Все результаты измерений, а также вычисленный по ним окончательный результат приводят вместе с погрешностью, которую выражают в тех же единицах, что и саму измеряемую величину, например: l = (1,572 ± 0,004) м. Среднее значение < x> необходимо округлять так, чтобы оно оканчивалось цифрой того же разряда, что и Δ х после её округления. Т.е. число и его погрешность всегда записывается так, чтобы их последние цифры принадлежали одному и тому же десятичному разряду. Значения погрешностей следует округлять, оставляя одну значащую цифру[3]. Округлять предпочтительно в сторону большего значения. Примеры: 1. Получено: U = 124,4 В; Δ U = 1,1 В. Следует записать: U = (124,4 ± 1,1) В. 2. Получено: V = 2,678•103 см/с; Δ V = 3,2 см/с. Следует записать: V = (2,678 ± 0,003) •103 cм/с. В промежуточных выкладках при расчете погрешностей нужно удерживать три-четыре значащие цифры. При представлении окончательных результатов физических измерений часто применяют запись числовых значений в виде десятичной дроби, умноженной на необходимую степень числа десять. Примеры: 1. При обработке группы результатов измерений получены: Результат округления записывают в виде: х = 965 ± 8. 2. При обработке группы результатов измерений получены: Результат округления записывают в виде: х = (38,9 ± 2,8)•104. 3. Числа 3106; 0,0285; 0,120 записывают так: 3,106•103; 2,85•10-2; 1,2•10-1. Графическое представление результатов эксперимента В ряде работ по результатам измерений требуется построить график. График строят на миллиметровой бумаге, либо на бумаге в клетку. Допускается компьютерное представление графика. Построение графика производится в следующем порядке: 1. Установить пределы измерения величин, откладываемых на координатных осях. 2. Выбрать масштаб по осям координат в зависимости от требуемой точности измерений. В качестве единицы измерения графика (клеточка или сантиметр на миллиметровой бумаге) следует брать только 10 n;2•10 n; 5•10 n единиц определяемой величины, где n –любое положительное или отрицательное число, начиная от нуля. 3. Масштаб выбирают с расчетом, чтобы поле графика приближалось к квадрату, а построенная прямая или кривая – к диагонали квадрата. 4. Выбирают начало координат. В начале координат могут стоят любые числа. 5. Наносят масштаб на координатные оси (на бумаге в клетку через 5 клеток, на миллиметровой бумаге – через 1, 2 или 5 см. Числа на координатных осях должны быть округленными. В конце координатных осей указывают величины, отложенные по осям координат, и единицы их измерения. 6. Наносят на график экспериментальные точки в виде крестиков, размах по высоте и ширине которых равен удвоенным погрешностям измерения, отложенным по осям величин. Значение координат точек на графике не пишут. Исключение делают только тогда, когда желают выделить какую-то точку. 7. Проводят при помощи лекала или линейки кривую или прямую, которая ближе всего подходит к экспериментальным точкам. Проведенная кривая является осреднением экспериментальных результатов. Поэтому экспериментальные точки могут быть как на кривой, так и под ней или над ней. 8. Проводя прямую линию (рис.1), нужно руководствоваться следующими правилами: · прямая должна пересечь все или почти все крестики, обозначающие систематические погрешности отложенных величин; · число точек, оказавшихся выше и ниже проведенной прямой, должно быть примерно одинаковым; · экспериментальные точки должны быть и выше, и ниже прямой во всем диапазоне значений x.
Рис.1. Прямая f = kx + b, проведенная через экспериментальные точки: а, б – неправильно; в, д – правильно; г – промах; Иногда через набор точек невозможно провести прямую, руководствуясь сформулированными правилами (рис.1 г, д). Если из общего набора выпадает только одна точка (рис.1 г), то ее следует считать промахом и в дальнейшем не учитывать. Если же сильно выбиваются несколько точек или явно видна нелинейность, то отсюда следует, что экспериментальные данные противоречат теоретической зависимости (f = kx + b). Если же наблюдаются случаи, показанные на рис.1 в или г, то можно сделать вывод, что экспериментальные данные подтверждают теоретическую зависимость. Лабораторная работа № 3
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 725; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.83.202 (0.009 с.) |

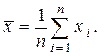 (1)
(1) .
. (2)
(2) (3)
(3) . (4)
. (4)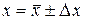 .
. .
.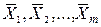 по формуле (1) и погрешности D X 1, D X 2,..., D X m по формуле (4) для доверительной вероятности Р = 0,95.
по формуле (1) и погрешности D X 1, D X 2,..., D X m по формуле (4) для доверительной вероятности Р = 0,95. .
.
 при средних значениях величин X 1, X 2, ..., Xm.
при средних значениях величин X 1, X 2, ..., Xm. .
. .
. .
.







