Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метрология - наука об измеренияхСодержание книги
Поиск на нашем сайте Метрология - наука об измерениях В практической жизни человек всюду имеет дело с измерениями. На каждом шагу встречаются измерения таких величин, как длина, объем, вес, время и др. Измерения являются одним из важнейших путей познания природы человеком. Они дают количественную характеристику окружающего мира, раскрывая человеку действующие в природе закономерности. Все отрасли техники не могли бы существовать без развернутой системы измерений, определяющих как все технологические процессы, контроль и управление ими, так и свойства и качество выпускаемой продукций. Велико значение измерений в современном обществе. Они служат не только основой научно-технических знаний, но имеют первостепенное значение для учета материальных ресурсов и планирования, для внутренней и внешней торговли, для обеспечения качества продукции, взаимозаменяемости узлов и деталей и совершенствования технологии, для обеспечения безопасности труда и других видов человеческой деятельности. Особенно возросла роль измерений в век широкого внедрения новой техники, развития электроники, автоматизации, атомной энергетики, космических полетов. Высокая точность управления полетами космических аппаратов достигнута благодаря современным совершенным средствам измерений, устанавливаемым как на самих космических аппаратах, так и в измерительно-управляющих центрах. Большое разнообразие явлений, с которыми приходится сталкиваться, определяет широкий круг величин, подлежащих измерению. Во всех случаях проведения измерений, независимо от измеряемой величины, метода и средства измерений, есть общее, что составляет основу измерений - это сравнение опытным путем данной величины с другой подобной ей, принятой за единицу. При всяком измерении мы с помощью эксперимента оцениваем физическую величину в виде некоторого числа принятых для нее единиц, т.е. находим ее значение. В настоящее время установлено следующее определение измерения: измерение есть нахождение значения физической величины опытным путем с помощью специальных технических средств. Отраслью науки, изучающей измерения, является метрология. Слово "метрология" образовано из двух греческих слов: метрон - мера и логос - учение. Дословный перевод слова "метрология" - учение о мерах. Долгое время метрология оставалась в основном описательной наукой о различных мерах и соотношениях между ними. С конца прошлого века благодаря прогрессу физических наук метрология получила существенное развитие. Большую роль в становлении современной метрологии как одной из наук физического цикла сыграл Д. И. Менделеев, руководивший отечественной метрологией в период 1892 - 1907 гг. Метрология в ее современном понимании - наука об измерениях, методах, средствах обеспечения их единства и способах достижения требуемой точности. Единство измерений - такое состояние измерений, при котором их результаты выражены в узаконенных единицах и погрешности измерений известны с заданной вероятностью. Единство измерений необходимо для того, чтобы можно было сопоставить результаты измерений, выполненных в разных местах, в разное время, с использованием разных методов и средств измерений. Точность измерений характеризуется близостью их результатов к истинному значению измеряемой величины. Таким образом, важнейшей задачей метрологии является усовершенствованием эталонов, разработкой новых методов точных измерений, обеспечение единства и необходимой точности измерений. Глава 2. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И ИХ ЕДИНИЦЫ Мелочи не играют решающей роли. Они решают всё Системы единиц физических величин Понятие о физической величине - одно из наиболее общих в физике и метрологии. Под физической величиной понимается свойство, общее в качественном отношении для многих физических объектов (физических систем, их состояний и происходящих в них процессов), но в количественном отношении индивидуальное для каждого объекта. Так, все тела обладают массой и температурой, но для каждого из них эти параметры различны. То же самое можно сказать и о других величинах - электрическом токе, вязкости жидкостей или потоке излучения. Для того чтобы можно было установить различия в количественном содержании свойств в каждом объекте, отображаемых физической величиной, вводится понятие размера физической величины. Исторически первой системой единиц физических величин была принятая в 1791 г. Национальным собранием Франции метрическая система мер. Она не являлась еще системой единиц в современном понимании, а включала в себя единицы длин, площадей, объемов, вместимостей и веса, в основу которых были положены две единицы: метр и килограмм. В 1832 г. немецкий математик К. Гаусс предложил методику построения системы единиц как совокупности основных и производных. Он построил систему единиц, в которой за основу были приняты три произвольные, независимые друг от друга единицы - длины, массы и времени. Все остальные единицы можно было определить с помощью этих трех. Такую систему единиц, связанных определенным образом с тремя основными, Гаусс назвал абсолютной системой. За основные единицы он принял миллиметр, миллиграмм и секунду. В дальнейшем с развитием науки и техники появился ряд систем единиц физических величин, построенных по принципу, предложенному Гауссом, базирующихся на метрической системе мер, но отличающихся друг от друга основными единицами. Рассмотрим главнейшие системы единиц физических величин [2]. Система СГС. Система единиц физических величин СГС, в которой основными единицами являются сантиметр как единица длины, грамм как единица массы и секунда как единица времени, была установлена в 1881 г. Система МКГСС. Применение килограмма как единицы веса, а в последующем как единицы силы вообще, привело в конце XIX века к формированию системы единиц физических величин с тремя основными единицами: метр - единица длины, килограмм-сила - единица силы и секунда - единица времени. Система МКСА. Основы этой системы были предложены в 1901 г. итальянским ученым Джорджи. Основными единицами системы МКСА являются метр, килограмм, секунда и ампер. Глава 3. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ) Хорошо спланировано - наполовину сделано Установление единой международной системы единиц Наличие ряда систем единиц физических величин, а также значительного числа внесистемных единиц, неудобства, связанные с пересчетом при переходе от одной системы единиц к другой, требовало унификации единиц измерений. Рост научно-технических и экономических связей между разными странами обусловливал необходимость такой унификации в международном масштабе. Требовалась единая система единиц физических величин, практически удобная и охватывающая различные области измерений. При этом она должна была сохранить принцип когерентности (равенство единице коэффициента пропорциональности в уравнениях связи между физическими величинами). В 1954 г. Х Генеральная конференция по мерам и весам установила шесть основных единиц (метр, килограмм, секунда, ампер, кельвин и свеча) практической системы единиц. Система, основанная на утвержденных в 1954 г. шести основных единицах, была названа Международной системой единиц, сокращенно СИ (SI - начальные буквы французского наименования Systeme International). Был утвержден перечень шести основных, двух дополнительных и первый список двадцати семи производных единиц, а также приставки для образования кратных и дольных единиц. Основные единицы СИ Основные единицы СИ с указанием сокращенных обозначений русскими и латинскими буквами приведены в табл. 1. Таблица 1
Определения основных единиц, соответствующие решениям Генеральной конференции по мерам и весам, следующие. Метр равен длине пути, проходимого светом в вакууме за 1/299792458 долю секунды. Килограмм равен массе международного прототипа килограмма. Секунда равна 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызывает на каждом участке проводника длиной 1 м силу взаимодействия, равную Кельвин равен 1/273.16 части термодинамической температуры тройной точки воды. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0.012 кг. Кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частотой Дополнительные единицы СИ Международная система единиц включает в себя две дополнительные единицы - для измерения плоского и телесного углов. Единица плоского угла - радиан (рад) - угол между двумя радиусами окружности, дуга между которыми по длине равна радиусу. В градусном исчислении радиан равен 57°17'48". Стерадиан (ср), принимаемый за единицу телесного угла, - телесный угол, вершина которого расположена в центре сферы и который вырезает на поверхности сферы площадь, равную площади квадрата со стороной, по длине равной радиусу сферы. Измеряют телесные углы путем определения плоских углов и проведения дополнительных расчетов по формуле
Телесному углу 1 ср соответствует плоский угол, равный 65°32', углу Дополнительные единицы СИ использованы для образования единиц угловой скорости, углового ускорения и некоторых других величин. Сами по себе радиан и стерадиан применяются в основном для теоретических построений и расчетов, так как большинство важных для практики значений углов (полный угол, прямой угол и т.д.) в радианах выражаются трансцендентными числами ( Производные единицы СИ Производные единицы Международной системы единиц образуются с помощью простейших уравнений между величинами, в которых числовые коэффициенты равны единице. Так, для линейной скорости в качестве определяющего уравнения можно воспользоваться выражением для скорости равномерного прямолинейного движения При длине пройденного пути (в метрах) и времени t, за которое пройден этот путь (в секундах), скорость выражается в метрах в секунду (м/с). Поэтому единица скорости СИ - метр в секунду - это скорость прямолинейно и равномерно движущейся точки, при которой она за время 1 с перемещается на расстояние 1 м. Если в определяющее уравнение входит числовой коэффициент, то для образования производной единицы в правую часть уравнения следует подставлять такие числовые значения исходных величин, чтобы числовое значение определяемой производной единицы было равно единице. Например, единица кинетической энергии СИ - килограмм-метр в квадрате на секунду в квадрате - это кинетическая энергия тела массой 2 кг, движущегося со скоростью 1 м/с, или кинетическая энергия тела массой 1 кг, движущегося со скоростью Кратные и дольные единицы Наиболее прогрессивным способом образования кратных и дольных единиц является принятая в метрической системе мер десятичная кратность между большими и меньшими единицами. В табл. 2 приводятся множители и приставки для образования десятичных кратных и дольных единиц и их наименования. Таблица 2
Следует учитывать, что при образовании кратных и дольных единиц площади и объема с помощью приставок может возникнуть двойственность прочтения в зависимоти от того, куда добавляется приставка. Так, сокращенное обозначение 1 км2 можно трактовать и как 1 квадратный километр и как 1000 квадратных метров, что, очевидно, не одно и то же (1 квадратный километр = 1.000.000 квадратных метров). В соответствии с международными правилами кратные и дольные единицы площади и объема следует образовывать, присоединяя приставки к исходным единицам. Таким образом, степени относятся к тем единицам, которые получены в результате присоединения приставок. Оценка с помощью интервалов Смысл оценки параметров с помощью интервалов заключается в нахождении интервалов, называемых доверительными, между границами которых с определенными вероятностями (доверительными) находятся истинные значения оцениваемых параметров. Вначале остановимся на определении доверительного интервала для среднего арифметического значения измеряемой величины. Предположим, что распределение результатов наблюдений нормально и известна дисперсия
Это означает, что истинное значение Q измеряемой величины с доверительной вероятностью Половина длины доверительного интервала
Полученный доверительный интервал, построенный с помощью среднего арифметического результатов n независимых повторных наблюдений, в Половина длины нового доверительного интервала
Теперь рассмотрим случай, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна. В этих условиях пользуются отношением
Плотность распределения этой дроби, впервые предсказанного Госсетом, писавшим под псевдонимом Стьюдент, выражается следующим уравнением:
Величины Таким образом, с помощью распределения Стьюдента по формуле (41) может быть найдена вероятность того, что отклонение среднего арифметического от истинного значения измеряемой величины не превышает
Пример. По результатам пяти наблюдений была найдена длина стержня. Итог измерений составляет L =15.785 мм, Из условия задачи следует, что имеются все основания для применения распределения Стьюдента. Вычисляем значение дроби Стьюдента
.
Для
Для
Пример. В условиях предыдущей задачи найти доверительную границу погрешности результата измерений для доверительной вероятности
При
В тех случаях, когда распределение случайных погрешностей не является нормальным, все же часто пользуются распределением Стьюдента с приближением, степень которого остается неизвестной. Кроме того, на основании центральной предельной теоремы теории вероятностей можно утверждать, что при достаточно большом числе наблюдений распределение среднего арифметического как суммы случайных величин Соотношения (38) показывают, что итог измерения не есть одно определенное число. В результате измерений мы получаем лишь полосу значений измеряемой величины. Смысл итога измерений, например, L =20.00±0.05 заключается не в том, что L = 20.00, как для простоты счи-тают, а в том, что истинное значение лежит где-то в границах от 19.95 до 20.05. К тому же нахождение внутри границ имеет некоторую вероятность, меньшую, чем единица, и, следовательно, нахождение вне границ не исключено, хотя и может быть очень маловероятным. Теперь найдем доверительные интервалы для дисперсии и среднеквадратического отклонения результатов наблюдений. Если распределение результатов наблюдений нормально, то отношение
Кривые плотности
Значения Пользуясь этой таблицей, можно найти доверительный интервал для оценки дисперсии результатов наблюдений при заданной доверительной вероятности. Этот интервал строится таким образом, чтобы вероятность выхода дисперсии за его границы не превышала некоторой малой величины q, причем вероятности выхода за обе границы интервала были бы равны между собой и составляли соответственно q /2 (рис.10).
Границы
Теперь, зная границы доверительного интервала для отношения
Пример. Даны результаты двадцати измерений длины Таблица 3
В качестве оценки математического ожидания длины детали принимаем ее среднее арифметическое
Точечная оценка среднеквадратического отклонения результатов наблюдений составляет:
Границы доверительного интервала для среднеквадратического отклонения результатов наблюдений находим по формуле (47):
В табл.П.6 приведены значения
где Тогда границы доверительного интервала для среднеквадратического отклонения результатов наблюдений при доверительной вероятности
Так, если в условиях предыдущей задачи среднеквадратическое отклонение определено на основании
Общие методы измерений Для точных измерений величин в метрологии разработаны приемы использования принципов и средств измерений, применение которых позволяет исключить из результатов измерений ряд систематических погрешностей и тем самым освобождает экспериментатора от необходимости определять многочисленные поправки для их компенсации, а в некоторых случаях вообще является предпосылкой получения сколько-нибудь достоверных результатов. Многие из этих приемов используют при измерении только определенных величин, однако существуют и некоторые общие приемы, названные методами измерения. Наиболее просто реализуется метод непосредственной оценки, заключающийся в определении величины непосредственно по отсчетному устройству измерительного прибора прямого действия, например взвешивание на циферблатных весах, определение размера детали с помощью микрометра или измерение давления пружинным манометром. Измерения с помощью этого метода проводятся очень быстро, просто и не требуют высокой квалификации оператора, поскольку не нужно создавать специальные измерительные установки и выполнять какие-либо сложные вычисления. Однако точность измерений чаще всего оказывается невысокой из-за погрешностей, связанных с необходимостью градуировки шкал приборов и воздействием влияющих величин (непостоянство температуры, нестабильность источников питания и пр.). При проведении наиболее точных измерений предпочтение отдается различным модификациям метода сравнения с мерой, при котором измеряемую величину находят сравнением с величиной, воспроизводимой мерой. Результат измерения либо вычисляют как сумму значения используемой для сравнения меры и показания измерительного прибора, либо принимают равным значению меры. Метод сравнения с мерой, заключающийся в том, что измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на измерительный прибор сравнения, с помощью которого устанавливается соотношение между ними, называется методом противопоставления. Примером этого метода является взвешивание груза на равноплечих весах, когда измеряемая масса определяется как сумма массы гирь, ее уравновешивающих. Применение метода противопоставления позволяет значительно уменьшить воздействие на результаты измерений влияющих величин, поскольку они более или менее одинаково искажают сигналы измерительной информации как в цепи преобразования измеряемой величины, так и в цепи преобразования величины, воспроизводимой мерой. Отсчетное устройство прибора сравнения реагирует на разность сигналов, вследствие чего эти искажения в некоторой степени компенсируют друг друга. Разновидностью метода сравнения с мерой является также нулевой метод измерения, который состоит в том, что подбором размера воспроизводимой мерой величины или путем ее принудительного изменения эффект воздействия сравниваемых величин на прибор сравнения доводят до нуля. В этом случае компенсация воздействий влияющих величин оказывается более полной, а значение измеряемой величины принимается равным значению меры. При дифференциальном методе измерения на измерительный прибор (не обязательно прибор сравнения) подается непосредственно разность измеряемой величины и величины, воспроизводимой мерой. Этот метод может быть использован, конечно, только в тех случаях, когда просто и точно реализуется операция вычитания величин (длины, перемещения, электрические напряжения). Дифференциальный метод неприменим при измерении таких величин, как температура или твердость тел. К разновидностям метода сравнения с мерой относится и метод замещения, широко применяемый в практике точных метрологических исследований. Сущность метода в том, что измеряемая величина замещается в измерительной установке некоторой известной величиной, воспроизводимой мерой. Замещение может быть полным или неполным, в зависимости от чего говорят о методе полного или неполного замещения. При полном замещении показания не изменяются и результат измерения принимается равным значению меры. При неполном замещении для получения значения измеряемой величины к значению меры следует прибавить величину, на которую изменилось показание прибора. Преимущество метода замещения - в последовательном во времени сравнении измеряемой величины и величины, воспроизводимой мерой. Благодаря тому, что обе эти величины включаются одна за другой в одну и ту же часть измерительной цепи прибора, точностные возможности измерений значительно повышаются по сравнению с измерениями, проводящимися с помощью других разновидностей метода сравнения, где несимметрия цепей, в которые включаются сравниваемые величины, приводит к возникновению систематических погрешностей. Способ замещения применяется при электрических измерениях с помощью мостов переменного тока, условие равновесия которых определяется не только значениями величин, воспроизводимых элементами плеч моста, но также и влиянием паразитных токов, емкостей, индуктивностей и рядом других факторов. Эти причины вызывают появление погрешностей, которые могут быть исключены, если проводить измерения методом замещения. Для этого вначале мост уравновешивается с включенной в его цепь измеряемой величиной, которая затем замещается известной величиной, и мост уравновешивается вновь. Если при этом никаких изменений ни в мосте, ни во внешних условиях не происходит, то указанные выше погрешности исключаются почти полностью. Одним из общих методов измерений является метод совпадений, представляющий собой разновидность метода сравнения с мерой. При проведении измерений методом совпадений разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов. По принципу метода совпадений построен нониус, входящий в состав ряда измерительных приборов. Так, например, шкала нониуса штангенциркуля имеет десять делений через 0.9 мм. Когда нулевая отметка шкалы нониуса оказывается между отметками основной шкалы штангенциркуля, это означает, что к целому числу миллиметров необходимо добавить число десятых долей миллиметра, равное порядковому номеру совпадающей отметки нониуса. В рамках перечисленных выше методов изм
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.015 с.) |

 Н.
Н. Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср. ([ср] – стерадиан. См. ниже.)
Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср. ([ср] – стерадиан. См. ниже.)
 - плоский угол при вершине конуса, образованного внутри сферы данным телесным углом.
- плоский угол при вершине конуса, образованного внутри сферы данным телесным углом. ср - плоский угол 120°, углу
ср - плоский угол 120°, углу  ср - плоский угол 180°.
ср - плоский угол 180°. и т.д.).
и т.д.). .
. м/с. Эта единица имеет особое наименование - джоуль (сокращенное обозначение Дж).
м/с. Эта единица имеет особое наименование - джоуль (сокращенное обозначение Дж).
 . Найдем вероятность попадания результата наблюдений в интервал
. Найдем вероятность попадания результата наблюдений в интервал  . Согласно формуле (29)
. Согласно формуле (29)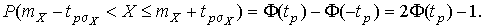

 ,
,
 находится между границами доверительного интервала
находится между границами доверительного интервала  .
. называется доверительной границей случайного отклонения результатов наблюдений, соответствующей доверительной вероятности Р. Для определения доверительной границы (при выполнении перечисленных условий) задаются доверительной вероятностью, например Р =0.95 или Р =0.995 и по формулам
называется доверительной границей случайного отклонения результатов наблюдений, соответствующей доверительной вероятности Р. Для определения доверительной границы (при выполнении перечисленных условий) задаются доверительной вероятностью, например Р =0.95 или Р =0.995 и по формулам
 интегральной функции нормированного нормального распределения. Затем по данным табл.П.3 приложения находят значение коэффициента
интегральной функции нормированного нормального распределения. Затем по данным табл.П.3 приложения находят значение коэффициента  и вычисляют доверительное отклонение
и вычисляют доверительное отклонение  (i =l, 2,..., n) распределены нормально, то нормально распределены и величины
(i =l, 2,..., n) распределены нормально, то нормально распределены и величины  , а значит, и среднее арифметическое
, а значит, и среднее арифметическое  , являющееся их суммой. Поэтому имеет место равенство
, являющееся их суммой. Поэтому имеет место равенство
 определяется по заданной доверительной вероятности Р.
определяется по заданной доверительной вероятности Р.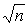 раз короче интервала, вычисленного по результату одного наблюдения, хотя доверительная вероятность для них одинакова. Это говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений.
раз короче интервала, вычисленного по результату одного наблюдения, хотя доверительная вероятность для них одинакова. Это говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений.


 вычисляют на основании опытных данных; они представляют собой точечные оценки математического ожидания и среднеквадратического отклонения результатов наблюдений.
вычисляют на основании опытных данных; они представляют собой точечные оценки математического ожидания и среднеквадратического отклонения результатов наблюдений.
 , согласно выражению (8), вычисляется по формуле
, согласно выражению (8), вычисляется по формуле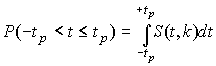
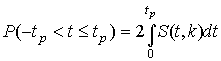
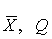 и
и  , получим окончательно
, получим окончательно .
.
 В табл.П.5 приведены значения
В табл.П.5 приведены значения  , например
, например  и т.д. Итог измерений записывается в виде
и т.д. Итог измерений записывается в виде
 =0.005 мм, причем существуют достаточно обоснованные предположения о том, что распределение результатов наблюдений было нормальным. Требуется оценить вероятность того, что истинное значение длины стержня отличается от среднего арифметического из пяти наблюдений не больше чем на 0.01 мм.
=0.005 мм, причем существуют достаточно обоснованные предположения о том, что распределение результатов наблюдений было нормальным. Требуется оценить вероятность того, что истинное значение длины стержня отличается от среднего арифметического из пяти наблюдений не больше чем на 0.01 мм.

 и
и  :
:  .
.
 .
.
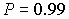 . По данным табл.П.5 при
. По данным табл.П.5 при  и, следовательно, доверительная граница:
и, следовательно, доверительная граница: мм.
мм.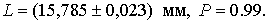
 , а практически уже при
, а практически уже при  распределение Стьюдента переходит в нормальное распределение и
распределение Стьюдента переходит в нормальное распределение и
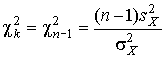
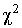 -распределение Пирсона с
-распределение Пирсона с  степенями свободы. Его дифференциальная функция распределения описывается формулой
степенями свободы. Его дифференциальная функция распределения описывается формулой
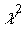 -распределения при различных значениях k, вычисленные по формуле (44), представлены на рис.9.
-распределения при различных значениях k, вычисленные по формуле (44), представлены на рис.9.
 , соответствующие различным вероятностям Р того, что отношение (43) в данном опыте будет меньше
, соответствующие различным вероятностям Р того, что отношение (43) в данном опыте будет меньше 
 и
и  такого доверительного интервала находят из равенства
такого доверительного интервала находят из равенства
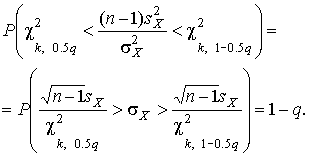
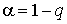 истинное значение
истинное значение  среднеквадратического отклонения результатов наблюдений лежит в интервале (
среднеквадратического отклонения результатов наблюдений лежит в интервале ( ], границы которого равны
], границы которого равны
 мм детали (табл.3).
мм детали (табл.3). мм.
мм. мм.
мм. , находим для числа степеней свободы
, находим для числа степеней свободы  в табл.П.6 приложения:
в табл.П.6 приложения:

 только при числах степеней свободы от 1 до 30. При k >30 можно пользоваться приближенной формулой
только при числах степеней свободы от 1 до 30. При k >30 можно пользоваться приближенной формулой
 по табл.П.3, в которой помещены значения интегральной функции нормированного нормального распределения.
по табл.П.3, в которой помещены значения интегральной функции нормированного нормального распределения. , равных
, равных
 измерений, то для
измерений, то для 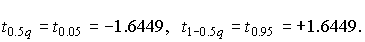
 составляют:
составляют: