
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Удельная и молярная теплоёмкостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Удельной теплоемкостью вещества называется физическая величина, численно равная количеству энергии в форме теплоты, которое надо сообщить единице массы этого вещества для увеличения его температуры на 1 Кельвин (т.е. это теплоёмкость, отнесённая к единице массы вещества):
В общем случае удельная теплоемкость зависит от рода вещества и от вида термодинамического процесса, в котором телу сообщается количество теплоты. Удельные теплоёмкости многих веществ приведены в справочниках (обычно для процесса при постоянном давлении). К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); Количество теплоты, поглощённой телом при изменении его состояния, зависит не только от начального и конечного состояний (в частности, от их температуры), но и от способа, которым был осуществлен процесс перехода между ними. Поэтому для газов различают два вида теплоемкостей: если газ нагревают, сохраняя его объем постоянным (изохорно), говорят об удельной теплоемкости газа при постоянном объеме c V; если же газ нагревают, сохраняя постоянным его давление (изобарно), то говорят об удельной теплоемкости газа при постоянном давлении с Р. У жидкостей и твёрдых тел разница между Ср и Cv сравнительно мала. Часто пользуются молярной теплоемкостью Сμ, которая, в отличие от удельной теплоемкости, отнесена не к единице массы (1 килограмму), а к массе одного моля вещества. Очевидно, что Cμ = m c, Дж/(моль×К) Для газов молярную теплоемкость, рассчитанную при постоянном давлении, обозначают С Р, а рассчитанную при постоянном объеме – С V. Следовательно, С Р = m× c P, C V = m× c V. Когда нагревание газа происходит при постоянном объеме, газ не совершает механической работы и все сообщаемое газу тепло идет только на увеличение его внутренней энергии D U, т.е.: D Q = m × c V×D T = D U. Если же нагревание газа происходит при постоянном давлении и, следовательно, объем газа увеличивается, то сообщаемое газу тепло D Q идет как на увеличение его внутренней энергии D U, так и на совершение газом работы D A над внешними телами, т.е. D Q = m × c P×D T = D U + D A. Из сопоставления формул следует, что c P > c V, т.е. удельная теплоемкость газа при постоянном давлении больше удельной теплоемкости того же газа при постоянном объеме. При этом, согласно уравнению Майера:
C P = C V + R. В данной работе требуется определить не абсолютные значения теплоемкостей газа, а их отношение, называемое коэффициентом Пуассона:
Теоретическое вычисление теплоемкости, в частности её зависимости от температуры тела, не может быть осуществлено с помощью чисто термодинамических методов и требует применения методов статистической физики. Теплоёмкость идеального газа Для газов вычисление теплоемкости сводится к вычислению средней энергии теплового движения отдельных молекул. Это движение складывается из поступательного и вращательного движений молекулы как целого и из колебаний атомов внутри молекулы.
На рис.1 изображена модель двухатомной молекулы. Молекула может совершать пять независимых движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y. Опыт показывает, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких температурах. При обычных температурах вращение около оси Z не происходит, так же как не вращается одноатомная молекула. Каждое независимое движение называется степенью свободы. Таким образом, одноатомная молекула имеет 3 поступательные степени свободы, «жесткая» двухатомная молекула имеет 5 степеней (3 поступательные и 2 вращательные), а многоатомная молекула – 6 степеней свободы (3 поступательные и 3 вращательные). В классической статистической физике доказывается так называемая теорема о равномерном распределении энергии по степеням свободы: если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна 1\2 kT, где k = 1,38×10- 23 Дж/К – постоянная Больцмана. Из этой теоремы следует, что молярные теплоемкости газа C p и C V и их отношение γ могут быть записаны в виде
где i – число степеней свободы молекулы газа. Для газа, состоящего из одноатомных молекул (i = 3):
Для газа, состоящего из двухатомных молекул (i = 5):
Для газа, состоящего из многоатомных молекул (i = 6):
Экспериментально измеренные теплоемкости многих газов при обычных условиях достаточно хорошо согласуются с приведенными выражениями. Однако, в целом классическая теория теплоемкости газов не может считаться вполне удовлетворительной. Существует много примеров значительных расхождений между теорией и экспериментом. Это объясняется тем, что классическая теория не в состоянии полностью учесть энергию, связанную с внутренними движениями в молекуле. Теорему о равномерном распределении энергии по степеням свободы можно применить и к тепловому движению частиц в твердом теле. Адиабатный процесс Основными параметрами, характеризующими состояние газа, являются давление P, объем V и температура Т. Связь между этими параметрами для идеального устанавливается уравнением Клапейрона-Менделеева:
где М – масса одного моль газа, кг/моль; m – масса газа, кг; Т – абсолютная температура газа, К; R = 8,31 Дж/(моль×К) – универсальная (молярная) газовая постоянная. Если известны два из трех основных параметров газа, то третий может быть выражен через них. При изменении всех трех параметров газа начальные параметры (p 1, V 1, T 1) связаны с новыми параметрами того же количества газа (p 2, V 2, T 2) равенством Адиабатный процесс — это процесс, происходящий без теплообмена системы с окружающей средой, т.е. Q = 0. Адиабатный процесс можно осуществить в системе, окруженной теплоизолирующей (адиабатной) оболочкой. Пример такого процесса — рабочий такт тепловой машины, при котором газ (пар) расширяется в цилиндре с теплоизолирующими стенками и поршнем, при отсутствии необратимых превращений работы трения в теплоту. Адиабатный процесс можно реализовать и при отсутствии адиабатной оболочки; для этого он должен протекать настолько быстро, чтобы за время процесса не произошло теплообмена между системой и окружающей средой. Первый закон термодинамики имеет вид:
Это значит, что при адиабатном процессе система может выполнять работу над внешними телами только за счет убыли своей внутренней энергии. Если А > 0, то Δ U = – A < 0, т.е. U 2 < U 1, а так как Как известно, газ совершает положительную работу, если Δ V > 0. Таким образом, при адиабатном расширении газ совершает работу и сам охлаждается. Наоборот, при адиабатном сжатии (А < 0) над газом совершается работа и газ нагревается. При адиабатном процессе давление и объем связаны между собой уравнением: p×V g = const или p×T g / (g – 1) = const, где γ > 1 — показатель адиабаты (или коэффициент Пуассона). Это уравнение называется уравнением адиабаты или уравнением Пуассона. Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит: d S = δ Q / T = 0 Здесь T – температура системы, δ Q – теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла. Адиабатное изменение состояния газа можно выразить графически. График этого процесса называют адиабатой (рис. 2). При одних и тех же начальных условиях (p 0, V 0) при адиабатном расширении давление газа уменьшается быстрее, чем при изотермическом, так как падение давления вызвано не только увеличением объема (как при изотермическом расширении), но и понижением температуры. Поэтому адиабата идет ниже изотермы и газ при адиабатном расширении совершает меньшую работу, чем при изотермическом расширении.
Рис. 2 При быстром сжатии (расширении) теплообмен произойти не успевает и процессы можно рассматривать как адиабатные (неравновесные). Поэтому любой газ при быстром сжатии нагревается (например, нагревание насоса при накачивании велосипедной шины). При сильном и быстром сжатии воздуха температура может повыситься настолько, что при наличии в воздухе паров бензина они воспламеняются. Это используется в дизельных двигателях для зажигания горючей смеси. Этим объясняется необходимость специального охлаждения мощных компрессоров. Охлаждение воздуха при адиабатном расширении вызывает образование облаков.
Теория лабораторной работы При быстром расширении или сжатии газа тепло не успевает пройти через стенки сосуда в окружающую среду, так что процесс такого расширения или сжатия близок к адиабатному. Давление газа при его сжатии растет как вследствие уменьшения объема, так и вследствие повышения его температуры, вызванного совершаемой над газом работой.
Для определения коэффициента Пуассона g используется наполненный воздухом стеклянный сосуд (рис. 3), соединенный с ручным нагнетательным насосом и манометром М. Кран К позволяет отключить насос от баллона и соединить баллон с внешней средой. Если с помощью насоса накачать в сосуд небольшое количество воздуха, то давление в нем повысится. Одновременно повысится и температура воздуха, но через несколько минут в результате теплообмена с окружающей средой температура воздуха в сосуде сравняется с температурой окружающей среды, т.е. станет равной Т 1, К. Назовем это состояние первым и обозначим его точкой 1 (рис. 4). Давление в сосуде в первом состоянии (при закрытом кране К и после того, как температура установится) р 1 = Р атм + h 1, где h 1 – разность между давлением в сосуде и атмосферным давлением, измеренная манометром и выраженная в тех же единицах измерения, что и Р атм. Удельный объем газа будет равен v 1 = V / m, где V – объем сосуда; m – масса газа в нем.
Если быстро открыть кран К, то часть воздуха из сосуда выйдет наружу, в результате чего произойдет адиабатное расширение воздуха, находящегося в сосуде. Кран К нужно закрыть, как только манометр покажет, что давление в сосуде сравнялось с атмосферным. Параметрами второго состояния воздуха в сосуде будут: давление р 2 = Р атм, Т 2 < Т 1, v 2 > v 1. Точка 2 на рис.4, характеризующая второе состояние воздуха, будет лежать на одной адиабате с точкой 1.
Через несколько минут после закрытия крана К в результате теплообмена с окружающей средой температура воздуха в сосуде станет равной температуре окружающего воздуха Т 3 = Т к. Удельный объем газа не изменится: v 3 = v 2, а давление в сосуде повысится до р 3 = Р атм + h 2. Избыточное давление h 2 должно быть записано по показанию манометра. Точка 3 на рис.4, характеризующая третье состояние воздуха в сосуде, лежит выше точки 2 на одной изохоре (линии постоянного объема) с ней. Точки 3 и 1 лежат на изотерме, которой соответствует температура Т 1. При адиабатном расширении, т.е. при переходе газа из состояния 1 в состояние 2, справедливо уравнение Пуассона. Из нашего опыта р 1 ×T к g / 1 – g = p 2 ×T 2 g / g – 1. (1) Для изохорного процесса перехода газа из второго состояния в третье получим
Подставив в уравнение (1) выражение
Прологарифмировав это уравнение, найдем (1– g)(lg р 1 –lg р 2) = g(lg р 2 –lg р 3), откуда Заменив величины р 1, р 2, р 3 уже известными выражениями, получим
Поскольку при больших значениях аргумента прирост логарифма пропорционален малому приросту аргумента, это уравнение можно упростить:
и определить коэффициент Пуассона по непосредственно измеренным в опыте величинам Р 1 и Р 2.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 3850; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.163.233 (0.009 с.) |

 , Дж/(кг×К)
, Дж/(кг×К) .
.

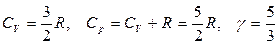


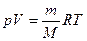 ,
, .
.
 , то T 2 < T 1.
, то T 2 < T 1.


 . (2)
. (2)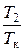 из (2), получим
из (2), получим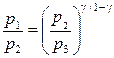 или
или  .
. .
.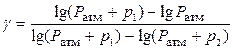
 (3)
(3)


