
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратимые и необратимые процессыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Первый закон термодинамики – закон сохранения энергии для тепловых процессов – устанавливает связь между количеством теплоты Q, полученной системой, изменением ΔU ее внутренней энергии и работой A, совершенной над внешними телами: Q = ΔU + A. Количество теплоты, сообщенное системе, идёт на изменение её внутренней энергии и на совершение работы протии внешних сил. Процессы, нарушающие первый закон термодинамики, никогда не наблюдались. Однако, этот закон не дает никаких сведений о том, в каком направлении развиваются процессы, удовлетворяющие принципу сохранения энергии. Различают обратимые и необратимые термодинамические процессы. Обратимым термодинамическим процессом называется процесс, допускающий возможность возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. При осуществлении обратимого процесса система переходит из одного равновесного состояния в другое. Процессы, в ходе которых система все время остается в состоянии равновесия, называются квазистатическими. Все квазистатические процессы обратимы. Все обратимые процессы являются квазистатическими. Если рабочее тело тепловой машины приводится в контакт с тепловым резервуаром, температура которого в процессе теплообмена остается неизменной, то единственным обратимым процессом будет изотермический квазистатический процесс, протекающий при бесконечно малой разнице температур рабочего тела и резервуара. При наличии двух тепловых резервуаров с разными температурами обратимым путем можно провести процессы на двух изотермических участках. Поскольку адиабатический процесс также можно проводить в обоих направлениях (адиабатическое сжатие и адиабатическое расширение), то круговой процесс, состоящий из двух изотерм и двух адиабат (цикл Карно) является единственным обратимым круговым процессом, при котором рабочее тело приводится в тепловой контакт только с двумя тепловыми резервуарами. Первый закон термодинамики не устанавливает направление тепловых процессов. Однако, как показывает опыт, многие тепловые процессы могут протекать только в одном направлении. Такие процессы называются необратимыми. Необратимым термодинамическим процессом называется процесс, не допускающий возможности возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Такой процесс в прямом направлении протекает самопроизвольно, а для осуществления его в обратном направлении так, чтобы система вернулась в первоначальное состояние, требуется компенсирующий процесс во внешних телах, в результате которого состояние этих тел оказывается отличным от первоначальных. Например, при тепловом контакте двух тел с разными температурами тепловой поток всегда направлен от более теплого тела к более холодному. Никогда не наблюдается самопроизвольный процесс передачи тепла от тела с низкой температурой к телу с более высокой температурой. Следовательно, процесс теплообмена при конечной разности температур является необратимым. Все остальные круговые процессы, проводимые с двумя тепловыми резервуарами, необратимы. Необратимыми являются процессы превращения механической работы во внутреннюю энергию тела из-за наличия трения, процессы диффузии в газах и жидкостях, процессы перемешивания газа при наличии начальной разности давлений и т. д. Все реальные процессы необратимы, но они могут сколь угодно близко приближаться к обратимым процессам. Обратимые процессы являются идеализацией реальных процессов. Односторонняя направленность макроскопических процессов психологически воспринимается как однонаправленность времени. Второй закон термодинамики Опыт показывает, что разные виды энергии неравноценны в отношении способности превращаться в другие виды энергии. Механическую энергию можно целиком превратить во внутреннюю энергию любого тела. Для обратных превращений внутренней энергии в другие виды энергии существуют определенные ограничения: запас внутренней энергии ни при каких условиях не может превратиться целиком в другие виды энергии. С отмеченными особенностями энергетических превращений связано протекание процессов в природе. Второй закон термодинамики связан непосредственно с необратимостью реальных тепловых процессов. Энергия теплового движения молекул качественно отличается от всех других видов энергии – механической, электрической, химической и т. д. Энергия любого вида, кроме энергии теплового движения молекул, может полностью превратиться в любой другой вид энергии, в том числе и в энергию теплового движения. Последняя может испытать превращение в любой другой вид энергии лишь частично. Поэтому любой физический процесс, в котором происходит превращение какого-либо вида энергии в энергию теплового движения молекул, является необратимым процессом, то есть он не может быть осуществлен полностью в обратном направлении. Общим свойством всех необратимых процессов является то, что они протекают в термодинамически неравновесной системе и в результате этих процессов замкнутая система приближается к состоянию термодинамического равновесия. Направление самопроизвольно протекающих процессов устанавливает второй закон (начало) термодинамики. Он может быть сформулирован в виде запрета на определенные виды термодинамических процессов. Этот закон представляет собой результат обобщения огромного числа опытных данных. Формулировки второго начала термодинамики: 1) по Карно: наибольший КПД тепловой машины не зависит от рода рабочего тела и вполне определяется предельными температурами, между которыми машина работает. 2) по Клаузиусу: невозможен процесс единственным результатом1 которого является передача энергии в форме теплоты от тела, менее нагретого, к телу, более нагретому. Второе начало термодинамики не запрещает переход теплоты от менее нагретого тела к более нагретому, такой переход осуществляется в холодильной машине, но при этом внешние силы совершают работу над системой, т.е. этот переход не является единственным результатом процесса. 3) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу. На первый взгляд может показаться, что такой формулировке противоречит процесс изотермического расширения идеального газа. Действительно, все полученное идеальным газом от какого-то тела тепло превращается полностью в работу. Однако получение тепла и превращение его в работу не единственный конечный результат процесса; кроме того, в результате процесса происходит изменение объема газа. 4) по Оствальду: осуществление вечного двигателя второго рода невозможно. Вечным двигателем второго рода называется периодически действующее устройство, которое совершает работу только за счет охлаждения одного источника теплоты. Примером такого двигателя мог бы служить судовой двигатель, получающий тепло из моря и использующий его для движения судна. Такой двигатель был бы практически вечным, т.к. запас энергии в окружающей среде практически безграничен. Все формулировки второго закона термодинамики эквивалентны. Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины, забрав тепло С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса. Таким образом, постулаты Клаузиуса и Томсона эквивалентны. Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения. С точки зрения статистической физики второе начало термодинамики имеет статистический характер: оно справедливо для наиболее вероятного поведения системы. Существование флуктуаций препятствует точному его выполнению, однако вероятность сколь-нибудь значительного нарушения крайне мала. Энтропия Энтропия (от греч. entropía — поворот, превращение), понятие, впервые введенное в термодинамику Р. Клаузиусом (1865) для определения меры необратимого рассеяния энергии, позволило строго математически сформулировать второй закон термодинамики. Энтропию можно определить с помощью двух эквивалентных подходов – статистического и термодинамического. Термодинамический подход Энтропия, функция состояния S термодинамической системы2, изменение которой dS для бесконечно малого обратимого изменения состояния системы равно отношению количества теплоты полученного системой в этом процессе (или отнятого от системы), к абсолютной температуре Т:
.где d S – приращение энтропии; δ Q 3 – минимальная теплота, подведенная к системе; T – абсолютная температура процесса. Величина dS является полным дифференциалом, т.е. ее интегрирование по любому произвольно выбранному пути дает разность между значениями энтропии в начальном (А) и конечном (В) состояниях:
Теплота не является функцией состояния, поэтому интеграл от δ Q зависит от выбранного пути перехода между состояниями А и В. Энтропия измеряется в Дж/(моль·К). Выражения (1) и (2) справедливы только для обратимых процессов. Для необратимых процессов выполняется неравенство:
из которого следует возрастания энтропии в этих процессах. Свойства энтропии: 1. Энтропия - величина аддитивная, т.е. энтропия системы из нескольких тел является суммой энтропий каждого тела: S = ∑Si . 2. В равновесных процессах без передачи тепла энтропия не меняется. Поэтому равновесные адиабатические процессы (δ Q = 0) называется изоэнтропийным. 3. Энтропия определяется только с точностью до произвольной постоянной. Действительно, согласно формуле (2) измеренной является лишь разность энтропий в двух состояниях. Абсолютное значение энтропии можно установить с помощью третьего начала термодинамики (теоремы Нернста): энтропия любого тела стремится к нулю при стремлении к абсолютному нулю его температуры: lim S = 0 при Т → 0К. Т.о., за начальную точку отсчета энтропии принимают S 0 = 0 при Т → 0 К. Энтропия – функция, устанавливающая связь между макро- и микро- состояниями; единственная функция в физике, которая показывает направленность процессов. Энтропия – в естественных науках мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике – мера вероятности осуществления какого-либо макроскопического состояния; в теории информации – мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса). Энтропия в информатике – степень неполноты, неопределённости знаний. Понятие энтропии как показал впервые Э. Шрёдингер (1944), существенно и для понимания явлений жизни. Живой организм с точки зрения протекающих в нём физико-химических процессов можно рассматривать как сложную открытую систему, находящуюся в неравновесном, но стационарном состоянии. Для организмов характерна сбалансированность процессов, ведущих к росту энтропии и процессов обмена, уменьшающих её. Однако жизнь не сводится к простой совокупности физико-химических процессов, ей свойственны сложные процессы саморегулирования. Поэтому с помощью понятия энтропии нельзя охарактеризовать жизнедеятельность организмов в целом. Закон возрастания энтропии
Рис.2. Применим неравенство (3) для описания необратимого кругового термодинамического процесса, изображенного на рис 2. Пусть процесс
Так как процесс
Подстановка этой формулы в неравенство (4) позволяет получить выражение:
Сравнение выражений (2) и (6) позволяет записать следующее неравенство:
в котором знак равенства имеет место в случае, если процесс Неравенство (7) может быть также записано и в дифференциальной форме:
Если рассмотреть адиабатически изолированную термодинамическую систему, для которой или в интегральной форме: /d S ≥ 0 (9) Из формулы (9) следует: S 2 ≥ S 1. Полученные неравенства выражают собой закон возрастания энтропии, который можно сформулировать следующим образом: В адиабатически изолированной термодинамической системе энтропия не может убывать: она или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс. Записанное утверждение является ещё одной формулировкой второго начала термодинамики. Таким образом, изолированная термодинамическая система стремится к максимальному значению энтропии, при котором наступает состояние термодинамического равновесия. Термодинамическому равновесию адиабатической системы соответствует состояние с максимумом энтропии. Энтропия может иметь не один, а несколько максимумов, при этом система будет иметь несколько состояний равновесия. Равновесие, которому соответствует наибольший максимум энтропии называется абсолютно устойчивым (стабильным). Из условия максимальности энтропии адиабатические системы в состоянии равновесия вытекает важное следствие: температура всех частей системы в состоянии равновесия одинакова. Рост энтропии является общим свойством всех самопроизвольно протекающих необратимых процессов в изолированных термодинамических системах. В состоянии равновесия энтропия принимает максимальное значение. В состоянии с максимальной энтропией макроскопические необратимые процессы невозможны. При обратимых процессах в изолированных системах энтропия не изменяется. Необходимо отметить, что если система не является изолированной, то в ней возможно уменьшение энтропии. Примером такой системы может служить, например, обычный холодильник, внутри которого возможно уменьшение энтропии. Но для таких открытых систем это локальное понижение энтропии всегда компенсируется возрастанием энтропии в окружающей среде, которое превосходит локальное ее уменьшение. Статистический подход В 1878 году Л. Больцман дал вероятностную трактовку понятия энтропии. Он предложил рассматривать энтропию как меру статистического беспорядка в замкнутой термодинамической системе. При этом Л. Больцман исходил из общего положения: природа стремится от состояний менее вероятных к состояниям более вероятным. Все самопроизвольно протекающие процессы в замкнутой системе, приближающие систему к состоянию равновесия и сопровождающиеся ростом энтропии, направлены в сторону увеличения вероятности состояния. Всякое состояние макроскопической системы, содержащей большое число частиц, может быть реализовано многими способами. Термодинамическая вероятность W состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние. По определению термодинамическая вероятность W >> 1. Например, если в сосуде находится 1 моль газа, то возможно огромное число N способов размещения молекулы по двум половинкам сосуда: N = 2 N Aгде N A – число Авогадро. Каждый из них является микросостоянием. Только одно из микросостояний соответствует случаю, когда все молекулы соберутся в одной половинке (например, правой) сосуда. Вероятность такого события практически равна нулю. Наибольшее число микросостояний соответствует равновесному состоянию, при котором молекулы равномерно распределены по всему объему. Поэтому равновесное состояние является наиболее вероятным. Равновесное состояние с другой стороны является состоянием наибольшего беспорядка в термодинамической системе и состоянием с максимальной энтропией. Согласно Больцману, энтропия S системы и термодинамическая вероятность W связаны между собой следующим образом: S = k lnW, где k = 1,38·10–23 Дж/К – постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Вероятностная трактовка второго закона термодинамики допускает самопроизвольное отклонение системы от состояния термодинамического равновесия. Такие отклонения называются флуктуациями 4. В системах, содержащих большое число частиц, значительные отклонения от состояния равновесия имеют чрезвычайно малую вероятность. Наличие флуктуаций показывает, что закон возрастания энтропии выполняется только статистически: в среднем для большого промежутка времени.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 9128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.216.248 (0.01 с.) |

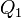 у нагревателя, отдав
у нагревателя, отдав 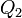 холодильнику и совершив при этом работу
холодильнику и совершив при этом работу 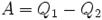 . После этого воспользуемся процессом Клаузиуса и вернем тепло
. После этого воспользуемся процессом Клаузиуса и вернем тепло 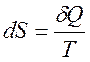 , (1)
, (1)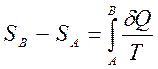 . (2)
. (2)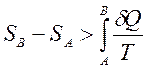 , (3)
, (3)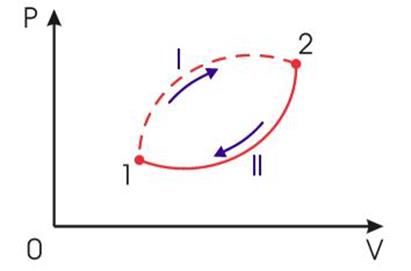
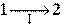 будет необратимым, а процесс
будет необратимым, а процесс  - обратимым. Тогда неравенство (3) для этого случая примет вид:
- обратимым. Тогда неравенство (3) для этого случая примет вид: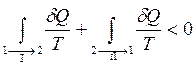 (4)
(4) (5)
(5)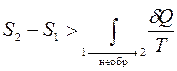 (6)
(6)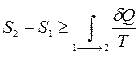 (7)
(7)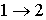 является обратимым, а знак больше, если процесс
является обратимым, а знак больше, если процесс 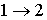 – необратимый.
– необратимый.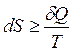 (8)
(8)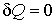 , то выражение (8) примет вид: Δ S = S 2 – S 1 ≥ 0
, то выражение (8) примет вид: Δ S = S 2 – S 1 ≥ 0


