
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термодинамические состояния и термодинамические процессыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В курсе механики было введено понятие физической системы (системы тел), для описания изменений которой используются законы динамики. Такую систему называют механической системой. Когда кроме законов механики требуется применение законов термодинамики, систему называют термодинамической системой. Термодинамика описывает макроскопические движения (изменения макроскопических состояний) термодинамической системы. Параметры, описывающие такое движение (изменения) термодинамической системы, принято разделять на внешние и внутренние. Это разделение весьма условно и зависит от конкретной задачи. Так, например, газ в воздушном шаре с эластичной оболочкой в качестве внешнего параметра имеет давление окружающего воздуха, а для газа в сосуде с жёсткой оболочкой внешним параметром является объём, ограниченный этой оболочкой. В термодинамической системе объём и давление могут изменяться независимо друг от друга. Для теоретического описания их изменения необходимо введение как минимум еще одного параметра - температуры. Изменения в системе описываются с помощью трёх термодинамических координат, связанных с соответствующими термодинамическими параметрами. Равновесным состоянием - состоянием термодинамического равновесия - называется такое состояния термодинамической системы, в котором отсутствуют всякие потоки (энергии, вещества, импульса и т.д.), а макроскопические параметры системы являются установившимися и не изменяются во времени. Классическая термодинамика утверждает, что изолированная термодинамическая система (предоставленная себе самой) стремится к состоянию термодинамического равновесия и после его достижения не может самопроизвольно из него выйти. Данное утверждение часто называю нулевым началом термодинамики. Системы, находящиеся в состоянии термодинамического равновесия, обладают следующими свойствами: Если две термодинамические системы, имеющие тепловой контакт, находятся в состоянии термодинамического равновесия, то и совокупная термодинамическая система находится в состоянии термодинамического равновесия. Если какая-либо термодинамическая система находится в термодинамическом равновесии с двумя другими системами, то и эти две системы находятся в термодинамическом равновесии друг с другом. Переход из одного термодинамического состояния в другое называется термодинамическим процессом. Предельным случаем квазиравновесного процесса является происходящий бесконечно медленно равновесный процесс, состоящий из непрерывно следующих друг за другом состояний термодинамического равновесия. Реально такой процесс протекать не может, однако если макроскопические изменения в системе происходят достаточно медленно (за промежутки времени, значительно превышающие время установления термодинамического равновесия), появляется возможность аппроксимировать реальный процесс квазистатическим (квазиравновесным). Такая аппроксимация позволяет проводить вычисления с достаточно высокой точностью для большого класса практических задач. Если в ходе термодинамического процесса система возвращается в исходное состояние, то такой процесс называется круговым или циклическим. Круговые процессы, также как и любые другие термодинамические процессы, могут быть как равновесными (а следовательно - обратимыми), так и неравновесными (необратимыми). При обратимом круговом процессе после возвращения термодинамической системы в исходное состояние в окружающих ее телах не возникает никаких термодинамических возмущений, и их состояния остаются равновесными. В этом случае внешние параметры системы после осуществления циклического процесса возвращаются к своим исходным значениям. При необратимом круговом процессе после его завершения окружающие тела переходят в неравновесные состояния и внешние параметры термодинамической системы изменяются. Динамическая система представляет собой математическую модель некоторого объекта, процесса или явления. Динамическая система также может быть представлена как система, обладающая состоянием. При таком подходе, динамическая система описывает (в целом) динамику некоторого процесса, а именно: процесс перехода системы из одного состояния в другое. Фазовое пространство системы — совокупность всех допустимых состояний динамической системы. Таким образом, динамическая система характеризуется своим начальным состоянием и законом, по которому система переходит из начального состояние в другое. Различают системы с дискретным временем и системы с непрерывным временем. В системах с дискретным временем, которые традиционно называются каскадами, поведение системы описывается последовательностью состояний. В системах с непрерывным временем, которые традиционно называются потоками, состояние системы определено для каждого момента времени на вещественной или комплексной оси. Динамическая система (как с дискретным, так и с непрерывным временем) часто описывается автономной системой дифференциальных уравнений, заданной в некоторой области и удовлетворяющей там условиям теоремы существования и единственности решения дифференциального уравнения. Положениям равновесия динамической системы соответствуют особые точки дифференциального уравнения, а замкнутые фазовые кривые — его периодическим решениям. Основное содержание теории динамических систем — это исследование кривых, определяемых дифференциальными уравнениями. Сюда входит разбиение фазового пространства на траектории и исследование предельного поведения этих траекторий: поиск и классификация положений равновесия, выделение притягивающих (аттракторы) и отталкивающих (репеллеры) множеств (многообразий). Важнейшие понятие теории динамических систем — это устойчивость (способность системы сколь угодно долго оставаться около положения равновесия или на заданном многообразии) и грубость (сохранение свойств при малых изменениях структуры динамической системы; «грубая система — это такая, качественный характер движений которой не меняется при достаточно малом изменении параметров»[1]). Б) Обращает на себя внимание поразительное сходство в поведении двух величин – энтропии и термодинамической вероятности: обе они участвуют при переходе системы к равновесию. Кроме этого, экспериментальные исследования показывают, что макроскопические свойства системы определяются ее микроскопическими свойствами. Поэтому естественно допустить существование связи между энтропией и термодинамической вероятностью.
Связь между термодинамической вероятностью состояния системы и ее энтропией была установлена в 1875 г. двумя знаменитыми учеными – Д. Гиббсом и Л. Больцманом. Эта связь выражается формулой Больцмана, которая имеет вид:
где Закон возрастания энтропии Применим неравенство Клаузиуса для описания необратимого кругового термодинамического процесса, изображенного на рис 3.13.
Пусть процесс
Так как процесс
Подстановка этой формулы в неравенство (3.55) позволяет получить выражение
Сравнение выражений (3.53) и (3.57) позволяет записать следующее неравенство
в котором знак равенства имеет место в случае, если процесс Неравенство (3.58) может быть также записано и в дифференциальной форме
Если рассмотреть адиабатически изолированную термодинамическую систему, для которой
или в интегральной форме
Полученные неравенства выражают собой закон возрастания энтропии, который можно сформулировать следующим образом: Принцип возрастания энтропии сводится к утверждению, что энтропия изолированных систем неизменно возрастает при всяком изменении их состояния и остается постоянной лишь при обратимом течении процессов Записанное утверждение является ещё одной формулировкой второго начала термодинамики. Таким образом, изолированная термодинамическая система стремится к максимальному значению энтропии, при котором наступает состояние термодинамического равновесия. Необходимо отметить, что если система не является изолированной, то в ней возможно уменьшение энтропии. Примером такой системы может служить, например, обычный холодильник, внутри которого возможно уменьшение энтропии. 13. а) Тепловой двигатель. Периодический тепловой двигатель. Рабочее тело. б) Используя графический метод, показать, что для работы периодического теплового двигателя незамкнутого процесса недостаточно. в) Какой процесс называют обратимым? Что такое нагреватель, холодильник? Какова их роль в работе теплового двигателя? г) Начертите и объясните схему превращения в тепловых двигателях внутренней энергии топлива в механическую работу. д) Как формулируют второе начало термодинамики? В чем состоит физический смысл этого закона?
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.178.145 (0.009 с.) |

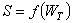 .
.
 ,
,
 , R – универсальная газовая постоянная, NA – число Авогадро.
, R – универсальная газовая постоянная, NA – число Авогадро.
 будет необратимым, а процесс
будет необратимым, а процесс  - обратимым. Тогда неравенство Клаузиуса для этого случая примет вид
- обратимым. Тогда неравенство Клаузиуса для этого случая примет вид .
.
 .
.
 .
.
 ,
,
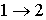 является обратимым, а знак больше, если процесс
является обратимым, а знак больше, если процесс  - необратимый.
- необратимый. .
.
 , то выражение (3.59) примет вид
, то выражение (3.59) примет вид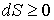
 .
.



