
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение состояния идеальных газовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Параметры состояния. Состояние системы (термодин) однозначно определяется совокупностью макроскопических среднестатистических величин, называемых параметрами состояния. Параметры, не зависящие от р-ров системы (темп), называют интенсивными. Зависящие – экстенсивные (объем). Внутр параметры (энергия, давление) определяются состоянием самой системы. Внешние определяют связь системы с окр средой. Если параметры с течением времени не меняются, то состояние системы – стационарное. Если нет еще и внутр потоков системы, вызванных, например, внешними полями, - равновесная. В ТТД рассматриваются равновесные системы и процессы переходов из одного равновесного состояния в другое. Процесс перехода из одного равнов сост в другое – термодинамический процесс. Главное допущение ТТД – то, что все равнов процессы явл обратимыми, т.е. если к системе приложить ту же силу в обратном направлении, она возвращается в первоначальное состояние. В ТТД обычно используется 3 основных параметра состояния, определенным образом зависящие друг от друга. Давление. (p). Обусловлено взаимодействием частиц рабочего тела с пов-тью и численно равно силе, действующей на единицу площади по нормали к этой пов-ти. (p [Па]). В соответствии с МКТ Температура. (Т) – статистическая физ величина, характеризующая степень нагретости тела. С точки зрения МКТ Удельный объем – v – объем единицы массы вещества.
2. Законы термодинамики (начала). 1 закон термодинамики. Энергия не возникает из ничего и не исчезает, а только переходит из одного вида в другой. Если обозначить индексами a,b,c различные виды энергии, а
Энергия – единая скалярная мера разл форм движения материи. Характеризует возможность системы совершать работу. Работа – мера взаимодействия систем, проявляющаяся при изменении энергии системы при переходе ее из одного равновесного сост в другое. Теплота – мера энергии хаот движения и взаимодействия частиц тела. Ту часть теплоты, кот можно превратить в др виды энергии при наличии разности температур между телами, называют тепловой энергией или кол-вом теплоты. Балансовое ур-е 1-го закона для удельных величин. Кол-во теплоты и работы (q и w) не явл ф-ями состояния рабочего тела, поэтому полные дифференциалы: В системе СИ все виды энергии и работа выражаются в Дж. 1 Дж - работа, производимая силой в 1 Н при перемещении тела в направлении действия силы на 1 м.
Термодинамический процесс
Смесь идеальных газов.
Задаться массовыми долями: Объемными долями: Молярными долями. Парциальный объем – объем, кот занимал бы этот газ, если бы его температуры и давление были как у смеси. Сумма объемных долей фактически равнозначна сумме молярных долей, кот обозначают как отношение кол-ва вещ-ва каждого газа к кол-ву вещ-ва смеси.
Теплоемкости газов.
Удельная массовая – к 1 кг вещ-ва. Удельная объемная – к 1 м3 Удельная мольная - к 1 моль. В термодинам расчетах обычно используют: Удельную теплоемкость при постоянном давлении: Удельную теплоемкость при постоянном объеме: В процессе при V=const теплота, сообщаемая газу, идет лишь на изменение его внутр энергии. А при p=const – и на изменение внутр энергии, и на совершение внешней работы. ( Истинная теплоемкость: Энтальпия.
Т.к. энтальпия – ф-я состояния, то ее можно описать 2-мя параметрами: Физический смысл. Рассм расширенную систему, включающую газ в цилиндре и поршень с грузом, общим весом G. (см рис). Энергия этой системы складывается из ее внутр энергии и потенциальной энергии поршня с грузом. В условиях равновесия G=pF. Выражая через параметры газа, получим:
Й закон термодинамики. 1824 – Карно – для превращения тепла в работу необходимо иметь два источника разной температуры. Парижская АН – невозможно создать вечный двигатель II рода, в котором подводимая извне теплота полностью превращается в работу (I рода – без затрат энергии). Клаузиус (1860) – теплота может переходить сама собой только от более нагретого тела к менее нагретому, для обратного перехода необходимо затратить работу. Томпсон (1861) – невозможно превратить в периодически действующем вечном двигателе работу в теплоту какого-либо тела, не производя никакого другого действия, кроме охлаждения тела. Больцман (1876) – все естественные процессы являются переходом от менее вероятного состояния к более вероятному. Энтропия. Феноменологическое определение Клаузиуса – существует источник теплоты с постоянной температурой Т и рабочее тело с температурой Т, к которому от источника обратимо подводится теплота dQ. Необходимо найти величину, кот характеризовала бы изменение состояния рабочего тела. Т.к. изменяется только Т и dQ, причем с повышением Т влияние dQ уменьшается: S=dQ/T. Если температура источника Ti больше температуры рабочего тела, то обратный переход теплоты от тела к источнику невозможен. Вероятностное определение Больцмана (закон возрастания энтропии). Рассмотрим систему, разделенную на 4 равные части и содержащую 8 частиц. (см рис). Для определения вероятностного состояния распределения частиц Планк вводит понятие термодинамической вероятности x=a lnW. Определение: термодинамическая вероятность – число микросостояний, т.е. распределений частиц в пространстве по скоростям и энергиям, с помощью которых может быть осуществлено данное макросостояние, которое оценивается обычными параметрами состояния (p,V,T). Она равна общему числу перестановок всех N частиц между собой, т.е. N!, деленному на число перестановок частиц внутри каждой из групп, входящих в их распределение (по скоростям и по энергиям). Т.е.
В отличие от 1-го закона, кот явл абсолютным законом природы, второй закон описывает системы, ограниченные статистическими законами и, следовательно, может нарушаться в отдельные моменты времени или в отдельных местах системы. Случаи нарушения 2-го закона термодинамики – флуктуация.
Физический смысл энтропии. Энтропия – мера ценности тепла: его работоспособности и технологической эффективности. Пусть рабочее тело получает от нагревателя с T1=const в обратимом процессе кол-во теплоты q1. Часть ее превращается в работу, а часть отдается окр среде с температурой Энтропия – мера потери работы вследствие необратимости реальных процессов. Чем более необратим процесс в изолированной системе, тем больше возрастает энтропия и тем больше доля энергии dq=TdS, не превращаясь в работу, рассеивается в окружающую среду – диссипация энергии. Энтропия – мера беспорядка. При подводе теплоты увеличивается хаотичность движения частиц и энтропия возрастает. Охлаждение при постоянном объеме – извлечение теплоты из тела, а, следовательно, и энтропии. Упорядоченность повышается, а энтропия уменьшается. Например, при конденсации газа упорядоченность изменяется скачкообразно, и так же скачкообразно понижается энтропия. При дальнейшем понижении Т жидкость замерзает, образуя жесткие связи между молекулами. Тепловая теорема Нернста (3-й закон термодинамики) – изменение энтропии при понижении температуры приближается к), но не может быть равно 0, т.к. понятие невозможности совершения работы соответствует понятию отсутствия движения, а, следовательно, и вещества.
Прямой цикл Карно. Имеется 1 горячий T1 и один холодный T2 источники теплоты. Теплоемкость каждого из них столь велика, что отъем рабочим телом теплоты от одного источника и передача ее другому практически не меняет их температуру. Единственным возможным осуществлением в этих условиях цикла (замкнутого процесса, т.е. когда тело, совершив работу, возвращается в первоначальное состояние и опять совершает работу): теплоту от горячего источника к рабочему телу нужно подвести изотермически, в любом другом случае температура рабочего тела будет меньше температуры источника, и процесс станет неравновесным. Чтобы равновесно охладить рабочее тело от температуры горячего до температуры холодного источника, не отдавая теплоты больше никакому другому телу, можно только путем адиабатного (т.е. без теплообмена с окр средой) расширения с совершением работы. Точно так же процесс теплоотдачи от рабочего тела к холодному источнику должен быть изотермическим, а процесс повышения Т с совершением работы – адиабатным сжатием. Т.е. такой цикл, состоящий из 2х адиабат и 2х изотерм, явл наиболее совершенным для превращения тепловой энергии в механическую. Газ (рабочее тело) с начальными параметрами в точке а помещен в цилиндр под поршень, причем боковые стенки цилиндра и поршень абсолютно изолированы так, что теплота может передаваться только через основание цилиндра. (см рис). Помещая этот цилиндр на тело с температурой Т1, газ начнет расширяться изотермически и поршень установится в положении b. (рис). В точке b подвод теплоты прекращаем и ставим цилиндр на теплоизоляцию. (рис). Тело продолжит расширяться, и цилиндр займет некое положение с. Т.к. вся система изолирована, этот процесс адиабатный (без изменения энтропии). Теперь возвратим тело в начальное состояние. Для этого сначала цилиндр поместим на холодный источник с температурой Т2. (рис). Т.к. темп расширенного тела и хол источника равна Т2, то работа сжатия w2 будет совершена в процессе при Т=Т2=const. При этом от рабочего тела к нижнему источнику поступит теплота q2=T2(S2-S1). Затем снова поставим цилиндр на теплоизолятор и дальнейшее сжатие проведем в условиях изоляции от окр среды, т.е. по адиабате. Вся работа, идущая на сжатие, превратится в изменение внутр энергии, в рез-те чего температура рабочего тела поднимется от Т2 до Т1. Т.о. в рез-те этого замкнутого процесса рабочее тело получит теплоту q1 и отдаст теплоту qq. следовательно, теплота цикла:
Диаграммы состояния. Т.к. ТТД – статистическая наука, то очень часто сложно описать математическим аппаратом тот или иной процесс. Поэтому очень удобно использовать графические методы решения задач. В зав-ти от имеющихся данных и желаемых рез-тов, используют различные системы координат:
pV диаграмма. Площадь под кривой процесса есть работа. TS диаграмма дает возможность непосредственно оценить кол-во теплоты, участвующей в процессе (под кривой процесса), а также направление теплового потока. При движении по кривой процесса вправо 9 в сторону возрастания энтропии) – подвод теплоты, а влево – отвод. HS – обычно для реальных газов (особенно для водяного пара) по экспериментальным данным. На них наносятся изотермы, изобары, изохоры, что позволяет определять для каждой точки процесса все параметры.
Термодинамические процессы. Все возможные термодин процессы изменения состояния ид газа, в кот скорость движения газа пренебрежимо мало, могут быть описаны одним уравнением при допущении, что процессы обратимы и теплоемкость при их протекании постоянна. Изохорный процесс. При ус ловии dv=0; v=const (см рис). В реальных процессах теплоемкость меняется, однако это изменение близкое к 0, прямо пропорционально зависимости от температуры. Поэтому обычно при расчете процессов используют значение средней арифметической теплоемкости в данном процессе: Изобарный процесс. Dp=0; p=const; Изотермический процесс.
Адиабатный процесс. Происходит без теплообмена с окр средой. Политропный процесс.
Т.е. политропный процесс в зав-ти от n охватывает всю совокупность термомеханических процессов идеальных газов. Для понимания направления процесса, их делят на группы соответственно значениям n. (см рис). З группы политропных процессов: При
Обратный цикл Карно. См рис. Рабочее телос нач параметрами в т. а расширяется адиабатно за счет собств внутр энергии, теряя при этом температуру от Т1 до Т2. Дальнейшее расширение идет по изотерме, и рабочее тело отбирает от нижнего источника с Т2 кол-во теплоты q2. Далее рабочее тело сжимают сначала по адиабате, при этом температура увеличивается с Т2 до Т1, а потом – по изотерме (Т1=const). При этом рабочее тело отдает верхнему источнику (с температурой Т1) кол-во теплоты q1. Т.к. сжатие происходит с температурой большей, чем температура расширения, работа сжатия будет больше работы расширения на величину площади цикла abcd в pv координатах. Эта работа превращается в теплоту и вместе с теплотой q2 передается верхнему источнику. Т.о., затратив работу lу, можно перенести теплоту от источника с меньшей температурой к источнику с большей. При этом нижний отдаст q2, а верхний получит Эксергия. Рассмотрим изолированную систему, состоящую из горячего источника с Т1 и холодного источника – окр среды с Т0, и рабочего тела, совершающего некий цикл. Работоспособностью – эксергией – теплоты Q1, отбираемой от горячего источника с Т1, называется максимальная полезная работа, которая может быть получена за счет этой теплоты при условии, что холодным источником является окр среда с Т0. Полезной называется та часть произведенной работы, которая может быть использована по нашему усмотрению, в отличие от полной работы расширения. Максимальная полезная работа – работа цикла Карно в диапазоне [T1; T0]. Потеря работоспособности – разность максимальной работы холодного и горячего источников.
TS диаграмма водяного пара. (см.рис.). TS диаграмма строится путем переноса значений из таблиц водяного пара. На оси Т откладывается тройная точка А (Т=273,16К, р=611Па). Откладывая значение энтропии для кипящей воды S’ и для сухого насыщенного пара S’’ при разных температурах получим пограничные кривые x=0; x=1. Влево от нижней пограничной кривой будет располагаться жидкость, между ними – влажный насыщенный пар, справа от верхней – перегретый пар. Ниже нулевой изотермы AB – лед+пар в равновесном состоянии. В области жидкости процесс нагрева воды от 0,01°С (273,16К) до температуры кипения проходит по кривой AaA’, практически совпадающей с нижней пограничной кривой жидкости (не совпадает т.к. вода – аномальная жидкость с макс плотностью при 4°С). практически все теплотехнические агрегаты работают при больших температурах, т.к. даже холодная сетевая вода не менее 7°С. на TS диаграмме наносят изобары (в области влажного пара совпадают с изотермами, в области перегретого пара - резко направляются вверх, имея точку изгиба на верхней пограничной кривой). В области влажного пара также наносятся линии равных степеней сухости. TS диаграмма удобна для нахождения энтропии, позволяет видеть изменение температуры в процессе и находить кол-во теплоты, участвующей в процессе (площадь под кривой процесса). Возможно нахождение работы цикла IS диаграмма водяного пара. Фактически рабочими параметрами водяного пара являются: энтропия (как мера кол-ва теплоты, отнесенное к температуре рабочего тела) и энтальпия (как полная энергия расширенного тела, коим и явл водяной пар). Т.е. в диаграмме iS техническая работа и кол-во теплоты, участвующей в процессе, будет изображаться не сложной площадью, как в TS диаграмме, а длиной линии, что значительно удобнее. Впервые iS диаграмма была предложена в 1904 г Молье. (см.рис). начало координат – тройная точка. По табл данным, откладывая для разных значний давлений энтальпию и энтропию для кипящей воды и сухого насыщ пара, получаем нижнюю и верхнюю пограничн кривые. Изобары в области влажного насыщ пара – пучок расходящихся прямых: 29.???
Рассмотрим движение газа через сопло. Т.к. оно предназначено для разгона потока (т.е. увеличения скорости dc>0), знак у приращения площади сечения dF определяется отношением скорости потока к скорости звука (а) в данном сечении. Если скорость потока мала Скорость истечения помимо геометрии сопла будет зависеть от отношения давления в сосуде p1 к давлению окр среды – внешнего давления р2. При каком-то р2/р1 , кот называют Для получения скоростей истечения больше скорости звука, нужно иметь давление за соплом меньше ркр. Для этого нужно резко уменьшить давление на выходе, т.е. для получения сверхзвуковой скорости сопло должно состоять из 2х частей: суживающейся (c<a) и расширяющейся (c>a). Такое сопло впервые было предложено шведским инженером Карлом Лавалем (1880) для получения сверхзвуковой скорости пара. В наст время основное применение – сопла реактивных двигателей. Угол расширения сопла 30. Процесс истечения iS диаграмме. При истечении реального газа (пара) при p>pкр, будут сказываться взаимодействия между молекулами, и в аналитические формулы надо будет добавить эти процессы. В этом случае они значительно усложнятся. Поэтому для процессов истечения реальных газов обычно используют iS диаграммы. (см.рис). Пусть пар с начальными параметрами р1 и Т1 вытекает в среду с давлением р2. Если пренебречь трением в сопле и передачей теплоты через стенку (большая скорость и хорошо спрофилированный канал), то этот процесс можно считать адиабатным (1-2 перпендик оси S) скорость истечения: Отношение потерь в сопле к располагаемому теплопадению называется коэф-том потерь энергии в сопле.
Влажный воздух Влажным воздухом называется смесь сухого насыщенного воздуха (не содержащего молекул воды) и влажного пара. По физ состоянию близок к идеальному газу. При данных давлениях и температуре может содержать разное кол-во водяного пара. Парциальное давление вод пара равно давлению насыщения при данной темп, если это насыщ влажный воздух. Кол-во пара в таком воздухе равно плотности сухого насыщенного пара Влажный воздух, кот не содержит при данном давлении и температуре максимально возможное кол-во водяного пара называется ненасыщенным, т.е. это смесь сухого воздуха и перегретого пара. Парц давление перегретого пара в смеси меньше давления насыщения при данной темп. Кол-во перегр пара в 1 м3 воздуха численно равно плотности перегретого пара, но меньше плотности насыщ пара. Охлаждая воздух, а следовательно и перегретый пар при данном давлении, можно довести перегретый пар до насыщения. Это будет тогда, когда темп воздуха станет равна темп насыщения при данном парц давлении водяного пара. Эта температура – температура точки росы
Параметры состояния. 2. Законы термодинамики (начала). Смесь идеальных газов. Теплоемкости газов. Энтальпия. Й закон термодинамики. Энтропия. Физический смысл энтропии. Прямой цикл Карно. Диаграммы состояния. Термодинамические процессы. Обратный цикл Карно. Эксе |
|||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 527; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.94.174 (0.016 с.) |

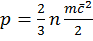
 – ср квадр скорость движ молекул. N – кол-во молекул в ед объема. Давление измеряется как разница внешнего (атмосферного) давления и давления рабочего тела. Если давление рабочего тела выше, то их разница называется манометрическим (избыточным) давлением.
– ср квадр скорость движ молекул. N – кол-во молекул в ед объема. Давление измеряется как разница внешнего (атмосферного) давления и давления рабочего тела. Если давление рабочего тела выше, то их разница называется манометрическим (избыточным) давлением. 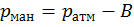 . Если наоборот – вакууметрическое.
. Если наоборот – вакууметрическое.  . В ТТД принято рассматривать только абсолютное давление.
. В ТТД принято рассматривать только абсолютное давление.  .
. k=1,38*10-23 Дж/К. в СИ [T]=1K. T=t+273,15K. Реперная точка t=0,01°С – точка существования в равновесном состоянии воды в 3-х фазах: жидкой, твердой и газообразной.
k=1,38*10-23 Дж/К. в СИ [T]=1K. T=t+273,15K. Реперная точка t=0,01°С – точка существования в равновесном состоянии воды в 3-х фазах: жидкой, твердой и газообразной. . величина, обратная уд объему
. величина, обратная уд объему  . Для сравнения величин, характеризующих системы в одинаковых состояниях, вводится понятие нормальных условий. Нормальные физ условия: p=760 мм.рт.ст =101,325кПа. Т=273,15К. Норм техн условия: p=736,5 мм.рт.ст.=98кПа, t=15°C.
. Для сравнения величин, характеризующих системы в одинаковых состояниях, вводится понятие нормальных условий. Нормальные физ условия: p=760 мм.рт.ст =101,325кПа. Т=273,15К. Норм техн условия: p=736,5 мм.рт.ст.=98кПа, t=15°C. - разность энергии в начале и в конце процесса, то
- разность энергии в начале и в конце процесса, то  . Изменение кол-ва энергии в термодин процессе всякой системы не зависит от характера (пути) этого процесса, а определяется как разность численных значений энергии в конце и начале процесса. Т.к. в ТТД рассматриваются взаимные превращения мех и тепл энергии, то мы можем записать
. Изменение кол-ва энергии в термодин процессе всякой системы не зависит от характера (пути) этого процесса, а определяется как разность численных значений энергии в конце и начале процесса. Т.к. в ТТД рассматриваются взаимные превращения мех и тепл энергии, то мы можем записать 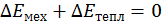 . для матем описания вводятся понятия:
. для матем описания вводятся понятия: w – работа, q- кол-во теплоты. Для всего тела:
w – работа, q- кол-во теплоты. Для всего тела:  – в дифф форме.
– в дифф форме. а
а 
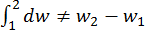
 сущ некая ф-я (ур-е состояния системы/рабочего тела). Если известно ур-е состояния, то для определения любого из параметров необходимо знать 2 других параметра. Если внешние условия изменяются, то изменяется и состояние системы. Совокупность изменений состояний термодин системы при переходе из одного равн сост в другое – термодинамический процесс.
сущ некая ф-я (ур-е состояния системы/рабочего тела). Если известно ур-е состояния, то для определения любого из параметров необходимо знать 2 других параметра. Если внешние условия изменяются, то изменяется и состояние системы. Совокупность изменений состояний термодин системы при переходе из одного равн сост в другое – термодинамический процесс. закон Дальтона. Парциальное давление – давление, кот имел бы каждый газ, входящий в смесь, если бы этот газ находился в том же количестве и в том же объеме и при той же температуре. pV=mRT. Чтобы задать смесь газов, можно:
закон Дальтона. Парциальное давление – давление, кот имел бы каждый газ, входящий в смесь, если бы этот газ находился в том же количестве и в том же объеме и при той же температуре. pV=mRT. Чтобы задать смесь газов, можно: …
… 
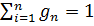

 …
… 

 . газовая постоянная смеси газов:
. газовая постоянная смеси газов: 
 отношение кол-ва теплоты
отношение кол-ва теплоты  , полученного телом при бесконечно малом изменении его состояния к связанному с этим изменению температуры тела dT, - теплоемкость тела в данном процессе. Обычно используют удельные теплоемкости, отнесенные к единице кол-ва вещ-ва:
, полученного телом при бесконечно малом изменении его состояния к связанному с этим изменению температуры тела dT, - теплоемкость тела в данном процессе. Обычно используют удельные теплоемкости, отнесенные к единице кол-ва вещ-ва:


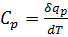

 - ур-е Майера.
- ур-е Майера.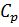 всегда больше
всегда больше  ). Для реальных газов
). Для реальных газов 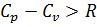 . Средней теплоемкостью процесса в интервале температур от
. Средней теплоемкостью процесса в интервале температур от 
 .
.
 . Значения теплоемкостей для различных вещ-в при различных температурах сведены в таблицы.
. Значения теплоемкостей для различных вещ-в при различных температурах сведены в таблицы. Дж. Т.к. все величины явл параметрами состояния, то Н будет некой ф-ей состояния термодин системы. Энтальпия обладает свойством аддитивности,
Дж. Т.к. все величины явл параметрами состояния, то Н будет некой ф-ей состояния термодин системы. Энтальпия обладает свойством аддитивности,  h=Н/м; Дж/кг
h=Н/м; Дж/кг . Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не зависит от хар-ра процесса.
. Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не зависит от хар-ра процесса. полная энергия расширенной системы – энтальпия. Учитывая, что
полная энергия расширенной системы – энтальпия. Учитывая, что  , а
, а  . если единственным видом работы системы явл работа расширения (
. если единственным видом работы системы явл работа расширения ( , то
, то 
 .
.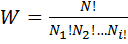 .
. для связи феноменологического и статистического определений рассматривают конечные объемы при расширении и конечные изменения энтропии.
для связи феноменологического и статистического определений рассматривают конечные объемы при расширении и конечные изменения энтропии. 
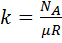
 . Чтобы процесс был обратимый,
. Чтобы процесс был обратимый,  тогда работа
тогда работа  , где
, где  . т.к. система изолирована, то
. т.к. система изолирована, то 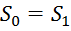 (
( . Тогда работа
. Тогда работа 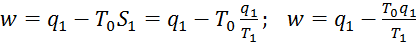 . Вывод: чем выше Т1, тем больше совершаемая системой работа, т.е. чем меньше энтропия, тем теплота ценнее. Если же температура рабочего тела равна тем окр среды, то работа совершаться не может при одном и том же кол-ве теплоты.
. Вывод: чем выше Т1, тем больше совершаемая системой работа, т.е. чем меньше энтропия, тем теплота ценнее. Если же температура рабочего тела равна тем окр среды, то работа совершаться не может при одном и том же кол-ве теплоты.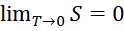
 равна площади abcd в TS координатах. Отношение работы, производимой двигателей за цикл, к кол-ву теплоты, подведенной за этот цикл (от горячего источника), называется термическим КПД цикла.
равна площади abcd в TS координатах. Отношение работы, производимой двигателей за цикл, к кол-ву теплоты, подведенной за этот цикл (от горячего источника), называется термическим КПД цикла. 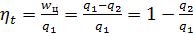 . Поставив значение q1, q2 для цикла Карно, имеем:
. Поставив значение q1, q2 для цикла Карно, имеем: 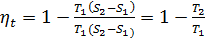 отсюда следует еще одно определение 2-го закона термодинамики: КПД цикла Карно зависит только от абсолютных температур горячего и холодного источника, т.е. увеличить его можно за счет снижения Т2 и/или увеличения Т1.
отсюда следует еще одно определение 2-го закона термодинамики: КПД цикла Карно зависит только от абсолютных температур горячего и холодного источника, т.е. увеличить его можно за счет снижения Т2 и/или увеличения Т1. – ур-е политропы.
– ур-е политропы.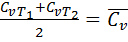 . Т.к. работа равна 0, то, в соответствии с 1м законом термодинамики, изменение внутр энергии равно кол-ву теплоты.
. Т.к. работа равна 0, то, в соответствии с 1м законом термодинамики, изменение внутр энергии равно кол-ву теплоты.  . Изменение энтропии
. Изменение энтропии  ;
; 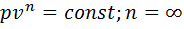
 (см.рис)
(см.рис) 

 . Т.к.
. Т.к.  , то изобара в TS координатах идет более полого, чем изохора.
, то изобара в TS координатах идет более полого, чем изохора.
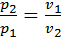 (см рис).
(см рис).  . Т.к. температура не меняется, то внутр энергия остается постоянной и, по 1-му закону термодинамики,
. Т.к. температура не меняется, то внутр энергия остается постоянной и, по 1-му закону термодинамики,  . При изотермическом сжатии работа, затраченная в этом процессе, происходит с отводом теплоты.
. При изотермическом сжатии работа, затраченная в этом процессе, происходит с отводом теплоты. 
 . (см рис).
. (см рис).  k – показатель адиабаты.
k – показатель адиабаты. 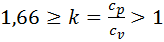 . Для одноатомного газа k=1,66; двухатомного k=1,4; трехатомного k=1,33.
. Для одноатомного газа k=1,66; двухатомного k=1,4; трехатомного k=1,33.  . Работа расширения, по 1 закону термодинамики, происходит за счет уменьшения внутр энергии.
. Работа расширения, по 1 закону термодинамики, происходит за счет уменьшения внутр энергии.  . Т.к.
. Т.к. 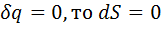 . А т.к.
. А т.к.  , то ПРОДОЛЖЕНИЕ 14 теплоемкость адиабатного процесса равна 0. Т.к. k>1, то изотерма идет более полого, чем адиабата.
, то ПРОДОЛЖЕНИЕ 14 теплоемкость адиабатного процесса равна 0. Т.к. k>1, то изотерма идет более полого, чем адиабата.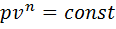

 ;
;  ;
;  ;
;  ;
;  ;
;  . Количество подведенной (отведенной) теплоты, по 1 закону, равно:
. Количество подведенной (отведенной) теплоты, по 1 закону, равно:  ;
;  ;
;  ;
;  ;
;  – теплоемкость в политропном процессе, а, т.к. n и k постоянны,
– теплоемкость в политропном процессе, а, т.к. n и k постоянны,  условно постоянна, то и
условно постоянна, то и 
 . Все процессы лежат между изохорой и изотермой. Расширение – с подводом теплоты, кот идет и на увеличение внутр энергии, и на совершение работы. С увеличением n доля теплоты, идущей на увеличение внутр энергии, уменьшается, а доля, идущая на совершение работы, увеличивается. Теплоемкость положительна.
. Все процессы лежат между изохорой и изотермой. Расширение – с подводом теплоты, кот идет и на увеличение внутр энергии, и на совершение работы. С увеличением n доля теплоты, идущей на увеличение внутр энергии, уменьшается, а доля, идущая на совершение работы, увеличивается. Теплоемкость положительна. . Графики располагаются между изотермой и адиабатой. Работа – за счет подводимой теплоты и уменьшения внутр энергии. С увеличением показателя n все большая часть работы, получается за счет уменьшения внутр энергии, и все меньшая – за счет подвода теплоты. Теплоемкость отрицательна.
. Графики располагаются между изотермой и адиабатой. Работа – за счет подводимой теплоты и уменьшения внутр энергии. С увеличением показателя n все большая часть работы, получается за счет уменьшения внутр энергии, и все меньшая – за счет подвода теплоты. Теплоемкость отрицательна. Графики располагаются между адиабатой и изохорой. При расширении газа процессы идут с уменьшением внутр энергии, с совершением работы и отводом теплоты. С увеличением n увеличивается доля теплоты, идущей на отвод … и уменьшается доля, идущая на совершение работы. Теплоемкость положительна. (см табл)
Графики располагаются между адиабатой и изохорой. При расширении газа процессы идут с уменьшением внутр энергии, с совершением работы и отводом теплоты. С увеличением n увеличивается доля теплоты, идущей на отвод … и уменьшается доля, идущая на совершение работы. Теплоемкость положительна. (см табл) . В настоящее время по обратному циклу работают 2 группы машин: холодильные установки, тепловые насосы.
. В настоящее время по обратному циклу работают 2 группы машин: холодильные установки, тепловые насосы. 
 – КПД цикла Карно. Отсюда:
– КПД цикла Карно. Отсюда:  . Часто полезную работу, полученную за счет
. Часто полезную работу, полученную за счет 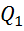 , представляют как разность:
, представляют как разность: 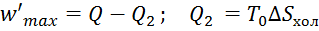 – теплота, отдаваемая холодному источнику.
– теплота, отдаваемая холодному источнику.  . Если бы в рассматриваемой системе протекали только равновесные процессы, то изменения энтропии не было бы, а увеличение энтропии хол источника равнялось бы уменьшению энтропии горячего источника.
. Если бы в рассматриваемой системе протекали только равновесные процессы, то изменения энтропии не было бы, а увеличение энтропии хол источника равнялось бы уменьшению энтропии горячего источника.  – для равновесных процессов.
– для равновесных процессов. . Величина
. Величина  определяет потерю работы, обусловленную рассеиванием энергии из-за необратимости реальных процессов. Чем больше неравномерность, тем меньше производимая системой работа.
определяет потерю работы, обусловленную рассеиванием энергии из-за необратимости реальных процессов. Чем больше неравномерность, тем меньше производимая системой работа. 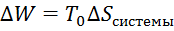 – уравнение Гюи-Стодолы.
– уравнение Гюи-Стодолы.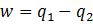 .
. . Угловой коэфф наклона изобары к оси абсцисс (S) в каждой точке диаграммы численно равен значению абсолютной температуры данного состояния.
. Угловой коэфф наклона изобары к оси абсцисс (S) в каждой точке диаграммы численно равен значению абсолютной температуры данного состояния.  .В области перегретого пара изобары уходят резко вверх. Температура растем (при пост давлении) с увеличением энтропии примерно по логарифмической кривой, и крутизна изобары увеличивается. При низких давл и относительно высоких темп перегретый пар по своим свойствам близок к ид газу, поэтому в этой области изотермы близки к горизонт прямым. При приближении к области насыщения перегретый пар приобретает св-ва реал газа, и кривая загибается. Обычно для технич расчетов всю диаграмму не изображают, а только ту ее часть, в диапазоне значений которой работает данный теплотехнический аппарат. Например паровой котел с рабочим давлением 12 бар обычно работает в диапазоне 60-100% (7-12 бар), соответственно и диаграмма изображается в этом диапазоне в области, близкой к сухому нас пару, а пароперегреватели в области перегрева. Для любой точки на этой диаграмме можно найти p, v, T, S, i, χ. Основные достоинства диаграммы в том, что кол-во теплоты в изобарном процессе равно разности ординат конечной и начальной точек процесса и будет изображаться отрезком вертикальной прямой, а не площадью.
.В области перегретого пара изобары уходят резко вверх. Температура растем (при пост давлении) с увеличением энтропии примерно по логарифмической кривой, и крутизна изобары увеличивается. При низких давл и относительно высоких темп перегретый пар по своим свойствам близок к ид газу, поэтому в этой области изотермы близки к горизонт прямым. При приближении к области насыщения перегретый пар приобретает св-ва реал газа, и кривая загибается. Обычно для технич расчетов всю диаграмму не изображают, а только ту ее часть, в диапазоне значений которой работает данный теплотехнический аппарат. Например паровой котел с рабочим давлением 12 бар обычно работает в диапазоне 60-100% (7-12 бар), соответственно и диаграмма изображается в этом диапазоне в области, близкой к сухому нас пару, а пароперегреватели в области перегрева. Для любой точки на этой диаграмме можно найти p, v, T, S, i, χ. Основные достоинства диаграммы в том, что кол-во теплоты в изобарном процессе равно разности ординат конечной и начальной точек процесса и будет изображаться отрезком вертикальной прямой, а не площадью.
 , то
, то  выделенное выражение отрицательно, значит dF<0, значит сопло сужается, и наоброт, если (c/a)>1, dF>0, значит сопло расширяется. (см.рис).
выделенное выражение отрицательно, значит dF<0, значит сопло сужается, и наоброт, если (c/a)>1, dF>0, значит сопло расширяется. (см.рис). , скорость истечения из сопла может достигнуть скорости звука. Если
, скорость истечения из сопла может достигнуть скорости звука. Если  , то скорость истечения меньше скорости звука. Внутри сопла скорость потока также везде меньше скорости звука, следовательно сопло должно сужаться по всей длине, а длина сопла определяет лишь потери на трение (не рассматриваем). Если
, то скорость истечения меньше скорости звука. Внутри сопла скорость потока также везде меньше скорости звука, следовательно сопло должно сужаться по всей длине, а длина сопла определяет лишь потери на трение (не рассматриваем). Если  . при меньшем угле с/а будет неоптимальным, а при большем угле угол раскрытия струи может стать меньше угла расширения и может произойти отрыв струи от стенок расширяющегося сопла. Т.о. между потоком и стенками образуется вакуум, следует возмущение потока (приграничные) следовательно сопротивление движению потока резко увеличится, следовательно поток затормозится. Рассмотрим движение газа через диффузор – канал, в котором давление повышается за счет уменьшения скоростного напора (dc<0). Если (с/а)<1, то dF>0, т.е. если скорость газа при входе в канал меньше скорости звука, то диффузор должен расширяться по направлению движения газа. Если (с/а)>1, то диффузор должен суживаться (dF<0).
. при меньшем угле с/а будет неоптимальным, а при большем угле угол раскрытия струи может стать меньше угла расширения и может произойти отрыв струи от стенок расширяющегося сопла. Т.о. между потоком и стенками образуется вакуум, следует возмущение потока (приграничные) следовательно сопротивление движению потока резко увеличится, следовательно поток затормозится. Рассмотрим движение газа через диффузор – канал, в котором давление повышается за счет уменьшения скоростного напора (dc<0). Если (с/а)<1, то dF>0, т.е. если скорость газа при входе в канал меньше скорости звука, то диффузор должен расширяться по направлению движения газа. Если (с/а)>1, то диффузор должен суживаться (dF<0).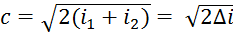 , где
, где  определяется как пересечение p1 и t1, а
определяется как пересечение p1 и t1, а 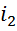 находят на пересечении вертикали из 1 с изобарой p2. В реальных условиях часть энергии будет затрачена на трение, т.е. диссипацию, и энтропия несколько увеличится (точка 2’’). При этом
находят на пересечении вертикали из 1 с изобарой p2. В реальных условиях часть энергии будет затрачена на трение, т.е. диссипацию, и энтропия несколько увеличится (точка 2’’). При этом  . В рез-те чего и скорость
. В рез-те чего и скорость  .
. .
.  – действительная скорость адиабатного неравновесного истечения. Каждое сопло в зав-ти от его профиля имеет свое значение
– действительная скорость адиабатного неравновесного истечения. Каждое сопло в зав-ти от его профиля имеет свое значение 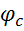 , которое хар-т эту скорость истечения
, которое хар-т эту скорость истечения 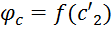 . В настоящее время для хорошо спрофилированных и обработанных сопел
. В настоящее время для хорошо спрофилированных и обработанных сопел  .
. . Общее давление влажного воздуха определяется по закону Дальтона:
. Общее давление влажного воздуха определяется по закону Дальтона:  . Масса пара в 1 м3 смеси газа называется абсолютной влажностью, кот численно равна плотности пара при его парциальном давлении рп и tсмеси. Если при пост температуре увеличивать влажность воздуха, то плотность нас пара будет возрастать. Если темп влажного воздуха ниже температуры насыщения водяного пара при давлении смеси, то предельной плотностью водяного пара будет плотность сухого насыщенного пара, при парц давлении меньшем, чем давление смеси. В этом предльном состоянии влажный воздух представляет собой смесь сухого воздуха и сухого насыщенного вод пара. Если темп влажного воздуха выше или равна темп насыщения водяного пара при давлении смеси, то процесс насыщения влажного воздуха водяным паром будет продолжаться, пока он не станет только сухим насыщенным водяным паром или не станет перегретым паром.
. Масса пара в 1 м3 смеси газа называется абсолютной влажностью, кот численно равна плотности пара при его парциальном давлении рп и tсмеси. Если при пост температуре увеличивать влажность воздуха, то плотность нас пара будет возрастать. Если темп влажного воздуха ниже температуры насыщения водяного пара при давлении смеси, то предельной плотностью водяного пара будет плотность сухого насыщенного пара, при парц давлении меньшем, чем давление смеси. В этом предльном состоянии влажный воздух представляет собой смесь сухого воздуха и сухого насыщенного вод пара. Если темп влажного воздуха выше или равна темп насыщения водяного пара при давлении смеси, то процесс насыщения влажного воздуха водяным паром будет продолжаться, пока он не станет только сухим насыщенным водяным паром или не станет перегретым паром.


