
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения состояния системы.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Каждому взаимодействию данного рода соответствует своя координата и свой потенциал. Для термодеформационной системы можно записать четвёрку параметров:
Если система имеет n степеней свободы (т.е. n взаимодействий различного рода), то для такой системы можно записать n координат x1, x2,…,xn и, соответственно, n потенциалов P1, P2,…,Pn. Совокупность координат и потенциалов общим числом 2n называется термодинамическими параметрами состояния системы. У этой системы две термодинамические степени свободы, а именно тепловая и деформационная. Как было установлено в ходе развития термодинамики, вся совокупность координат состояния системы полностью характеризует состояние системы. Например, внутренняя энергия системы U = U(x1, x2,…,xn) является однозначной функцией. Потенциалы, в свою очередь, являются однозначными функциями всей совокупности координат состояния системы, т.е. Pk = Pk(x1, x2,…,xn) (4) Уравнение (4) называется уравнением состояния системы в общем виде. Пример. Рассмотрим термодеформационную систему Уравнение (4) для этого случая запишется в виде двух уравнений: T = T(S, v), P = P(S, v). Так как энтропия на опыте не определяется, и приборов для измерения энтропии нет в природе, то желательно энтропию из этих состояний системы исключить. Для этого выразим её из первого и подставим во второе уравнение. Состояния сведём к одному уравнению F(p, T, v) = 0 (5) Тогда система уравнений сведется к одному уравнению. Уравнение (5) -уравнение состояния термодеформационной системы в общем виде. Конкретный вид этого уравнении состояния системы термодинамика в силу своего аппарата получить не может и вынуждена заимствовать его у других наук. Это проявление слабости классической термодинамики обусловлено на ее макроскопичности. Из физики известно множество уравнений удовлетворяющих уравнению (5). Самое просто из них: pv = RT (6) Уравнение (6)- уравнение состояния идеального газа.(уравнение Менделеева-Клайперона). В этом уравнении: Р(Па)- абсолютное давление, v( R – удельная газовая постоянная. R = Примечание. Во всех уравнениях термодинамики используется только абсолютное давление. Удельная газовая постоянная связана с универсальной газовой постоянной R = Здесь Rμ=8341 Например, для воздуха у которого молекулярная масса μвоздуха = 28,96. Значение удельной газовой постоянной содержится в справочной литературе или вычисляется по формуле (7). Идеальный газ – газ, молекулы которого не имеют объёма (материальные точки), между ними отсутствуют силы межмолекулярного притяжения и эти молекулы не образуют ассоциации молекул. Идеальный газ это научная абстракция. Любой газ в зависимости от его давления и температуры может считаться либо условно идеальным, либо сугубо реальным. При малых давлениях и высоких температурах любой газ можно условно считать идеальным и применять к нему уравнение Менделеева-Клапейрона. При давлениях не превышающих 3МПа и температурах превышающих -50̊ С для любого газа можно применить уравнение (6). Чем выше давление и ниже температура, тем больше свойства газа отклоняются от свойств идеального газа, тем больше погрешность, получаемая при использовании уравнения Менделеева-Клапейрона. Погрешности вычислений состояния реального газа с помощью уравнения (6) в области давлений превышающих 3 МПа не должны превышать погрешность измерений. Уравнения состояния идеального газа в форме (6) было получено Клапейроном. Менделеевым, уравнение состояния идеального газа было получено в следующем виде: pvμ = RμT (8) здесь vμ – молярный объём, Rμ – универсальная газовая постоянная. Молярный объем- это объем занимаемый одним кмолем вещества. 1 кмоль- количество вещества в кг численно равная его молекулярной массе поэтому удельный и молярный объемы связаны между собой соотношением:
Если подставить в уравнение pvμ = RμT, R = Уравнение (6) и (8) были получены их авторами независимо друг от друга. Для идеального газа известно только одно уравнение состояния- это уравнение Менделеева-Клапейрона, которое может быть записано в различных формах. 1) pvμ = RμT 2) pW = MRT (10) 3) P=rRT (11) 4)
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 649; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.142.42 (0.009 с.) |

 P
P
 - индивидуальная характеристика газа. Rвоздуха = 287
- индивидуальная характеристика газа. Rвоздуха = 287  .
.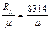 (7)
(7) - Универсальная газовая постоянная
- Универсальная газовая постоянная (9)
(9) и v=
и v=  , получим уравнение pv = RT
, получим уравнение pv = RT ,где
,где  (12)
(12)


